FP-IRL: Fokker-Planck-based Inverse Reinforcement Learning -- A Physics-Constrained Approach to Markov Decision Processes

Inverse Reinforcement Learning (IRL) is a compelling technique for revealing the rationale underlying the behavior of autonomous agents. IRL seeks to estimate the unknown reward function of a Markov decision process (MDP) from observed agent trajectories. However, IRL needs a transition function, and most algorithms assume it is known or can be estimated in advance from data. It therefore becomes even more challenging when such transition dynamics is not known a-priori, since it enters the estimation of the policy in addition to determining the system's evolution. When the dynamics of these agents in the state-action space is described by stochastic differential equations (SDE) in It^{o} calculus, these transitions can be inferred from the mean-field theory described by the Fokker-Planck (FP) equation. We conjecture there exists an isomorphism between the time-discrete FP and MDP that extends beyond the minimization of free energy (in FP) and maximization of the reward (in MDP). We identify specific manifestations of this isomorphism and use them to create a novel physics-aware IRL algorithm, FP-IRL, which can simultaneously infer the transition and reward functions using only observed trajectories. We employ variational system identification to infer the potential function in FP, which consequently allows the evaluation of reward, transition, and policy by leveraging the conjecture. We demonstrate the effectiveness of FP-IRL by applying it to a synthetic benchmark and a biological problem of cancer cell dynamics, where the transition function is inaccessible.

Machine learning in quantum computers via general Boltzmann Machines: Generative and Discriminative training through annealing

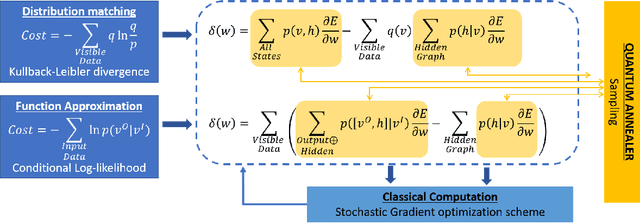
We present a Hybrid-Quantum-classical method for learning Boltzmann machines (BM) for generative and discriminative tasks. Boltzmann machines are undirected graphs that form the building block of many learning architectures such as Restricted Boltzmann machines (RBM's) and Deep Boltzmann machines (DBM's). They have a network of visible and hidden nodes where the former are used as the reading sites while the latter are used to manipulate the probability of the visible states. BM's are versatile machines that can be used for both learning distributions as a generative task as well as for performing classification or function approximation as a discriminative task. We show that minimizing KL-divergence works best for training BM for applications of function approximation. In our approach, we use Quantum annealers for sampling Boltzmann states. These states are used to approximate gradients in a stochastic gradient descent scheme. The approach is used to demonstrate logic circuits in the discriminative sense and a specialized two-phase distribution using generative BM.