Machine learning in quantum computers via general Boltzmann Machines: Generative and Discriminative training through annealing

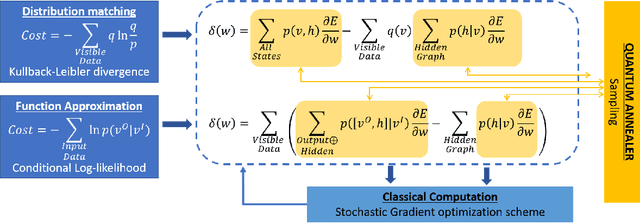
We present a Hybrid-Quantum-classical method for learning Boltzmann machines (BM) for generative and discriminative tasks. Boltzmann machines are undirected graphs that form the building block of many learning architectures such as Restricted Boltzmann machines (RBM's) and Deep Boltzmann machines (DBM's). They have a network of visible and hidden nodes where the former are used as the reading sites while the latter are used to manipulate the probability of the visible states. BM's are versatile machines that can be used for both learning distributions as a generative task as well as for performing classification or function approximation as a discriminative task. We show that minimizing KL-divergence works best for training BM for applications of function approximation. In our approach, we use Quantum annealers for sampling Boltzmann states. These states are used to approximate gradients in a stochastic gradient descent scheme. The approach is used to demonstrate logic circuits in the discriminative sense and a specialized two-phase distribution using generative BM.