Geometric Neural Operators (GNPs) for Data-Driven Deep Learning of Non-Euclidean Operators

We introduce Geometric Neural Operators (GNPs) for accounting for geometric contributions in data-driven deep learning of operators. We show how GNPs can be used (i) to estimate geometric properties, such as the metric and curvatures, (ii) to approximate Partial Differential Equations (PDEs) on manifolds, (iii) learn solution maps for Laplace-Beltrami (LB) operators, and (iv) to solve Bayesian inverse problems for identifying manifold shapes. The methods allow for handling geometries of general shape including point-cloud representations. The developed GNPs provide approaches for incorporating the roles of geometry in data-driven learning of operators.

SDYN-GANs: Adversarial Learning Methods for Multistep Generative Models for General Order Stochastic Dynamics

We introduce adversarial learning methods for data-driven generative modeling of the dynamics of $n^{th}$-order stochastic systems. Our approach builds on Generative Adversarial Networks (GANs) with generative model classes based on stable $m$-step stochastic numerical integrators. We introduce different formulations and training methods for learning models of stochastic dynamics based on observation of trajectory samples. We develop approaches using discriminators based on Maximum Mean Discrepancy (MMD), training protocols using conditional and marginal distributions, and methods for learning dynamic responses over different time-scales. We show how our approaches can be used for modeling physical systems to learn force-laws, damping coefficients, and noise-related parameters. The adversarial learning approaches provide methods for obtaining stable generative models for dynamic tasks including long-time prediction and developing simulations for stochastic systems.

GD-VAEs: Geometric Dynamic Variational Autoencoders for Learning Nonlinear Dynamics and Dimension Reductions

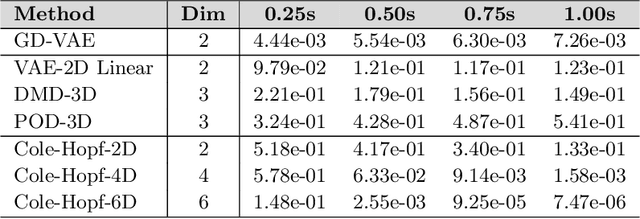
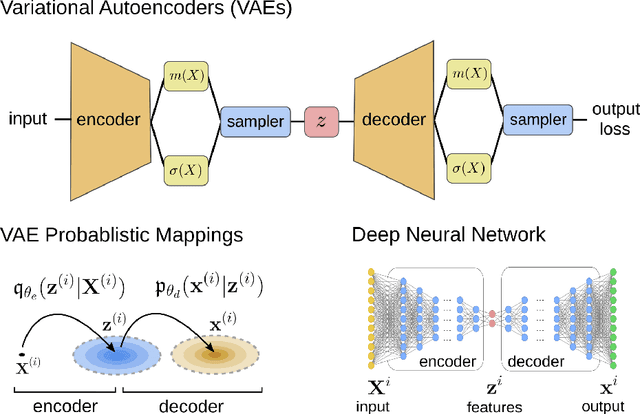
We develop data-driven methods incorporating geometric and topological information to learn parsimonious representations of nonlinear dynamics from observations. We develop approaches for learning nonlinear state space models of the dynamics for general manifold latent spaces using training strategies related to Variational Autoencoders (VAEs). Our methods are referred to as Geometric Dynamic (GD) Variational Autoencoders (GD-VAEs). We learn encoders and decoders for the system states and evolution based on deep neural network architectures that include general Multilayer Perceptrons (MLPs), Convolutional Neural Networks (CNNs), and Transpose CNNs (T-CNNs). Motivated by problems arising in parameterized PDEs and physics, we investigate the performance of our methods on tasks for learning low dimensional representations of the nonlinear Burgers equations, constrained mechanical systems, and spatial fields of reaction-diffusion systems. GD-VAEs provide methods for obtaining representations for use in learning tasks involving dynamics.

MLMOD Package: Machine Learning Methods for Data-Driven Modeling in LAMMPS

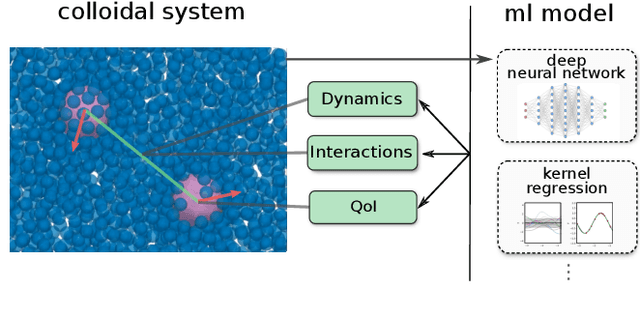
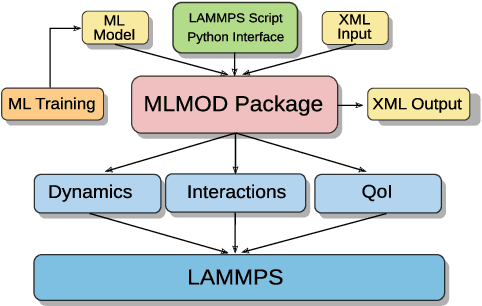
We discuss a software package for incorporating into simulations data-driven models trained using machine learning methods. These can be used for (i) modeling dynamics and time-step integration, (ii) modeling interactions between system components, and (iii) computing quantities of interest characterizing system state. The package allows for use of machine learning methods with general model classes including Neural Networks, Gaussian Process Regression, Kernel Models, and other approaches. We discuss in this whitepaper our prototype C++ package, aims, and example usage.

Variational Autoencoders for Learning Nonlinear Dynamics of Physical Systems

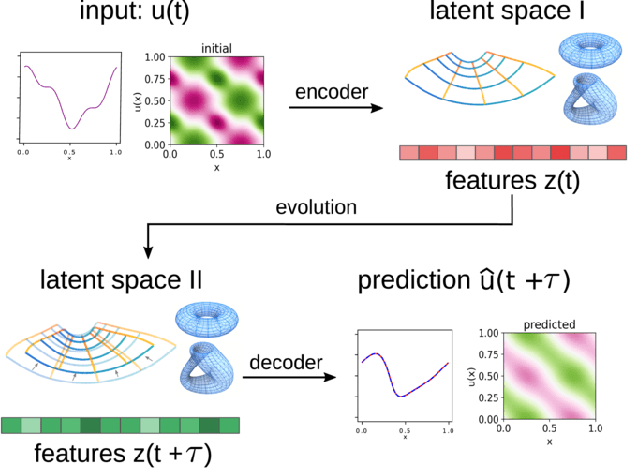
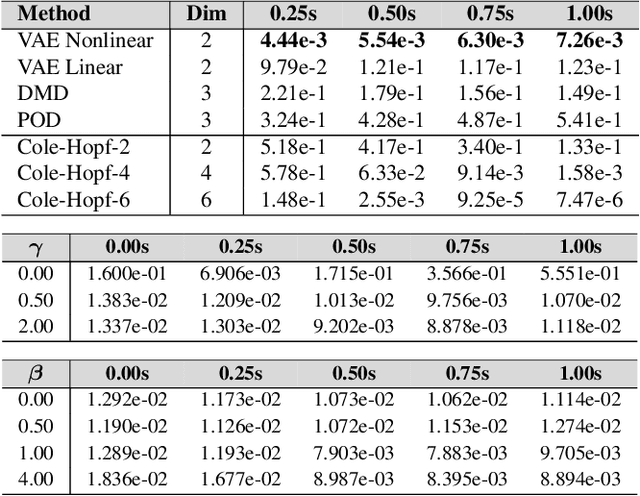
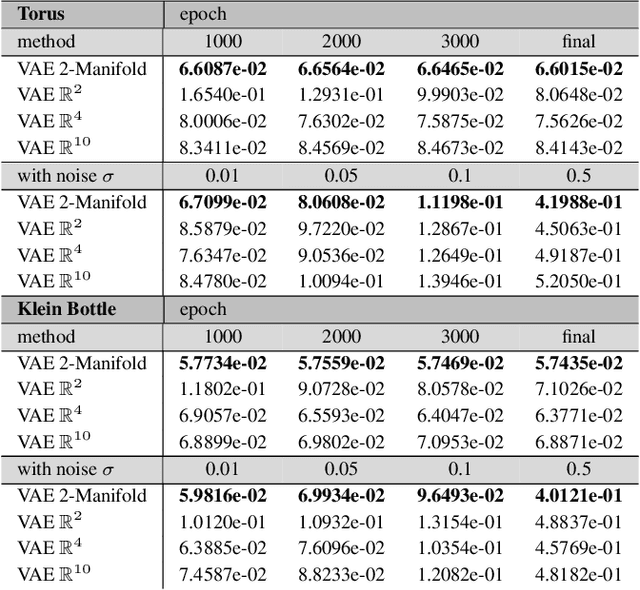
We develop data-driven methods for incorporating physical information for priors to learn parsimonious representations of nonlinear systems arising from parameterized PDEs and mechanics. Our approach is based on Variational Autoencoders (VAEs) for learning from observations nonlinear state space models. We develop ways to incorporate geometric and topological priors through general manifold latent space representations. We investigate the performance of our methods for learning low dimensional representations for the nonlinear Burgers equation and constrained mechanical systems.

GMLS-Nets: A framework for learning from unstructured data

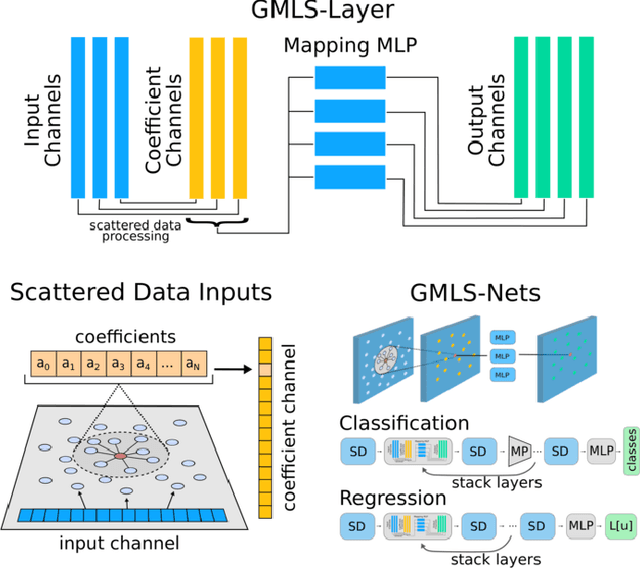
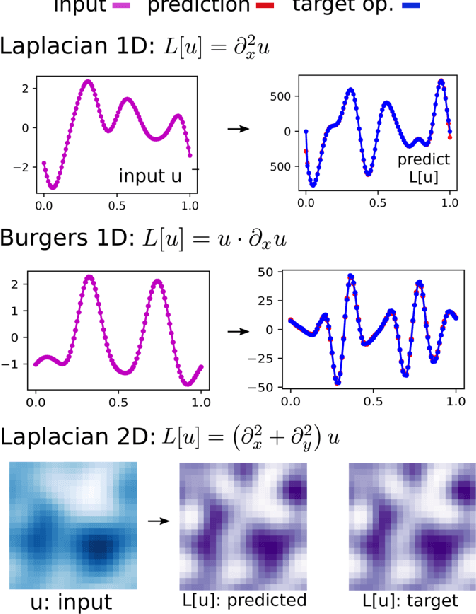
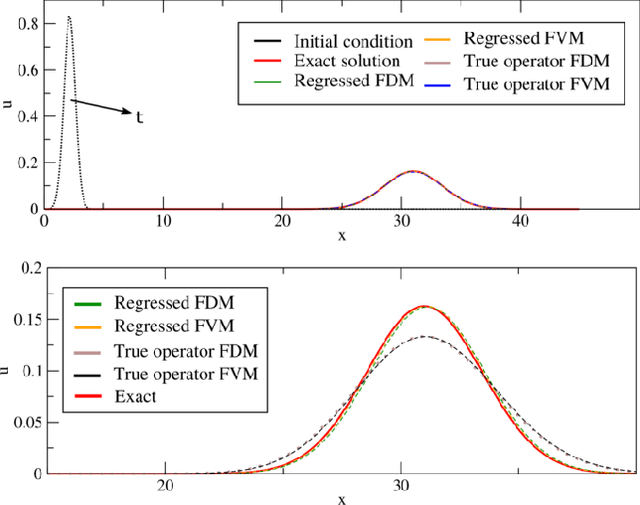
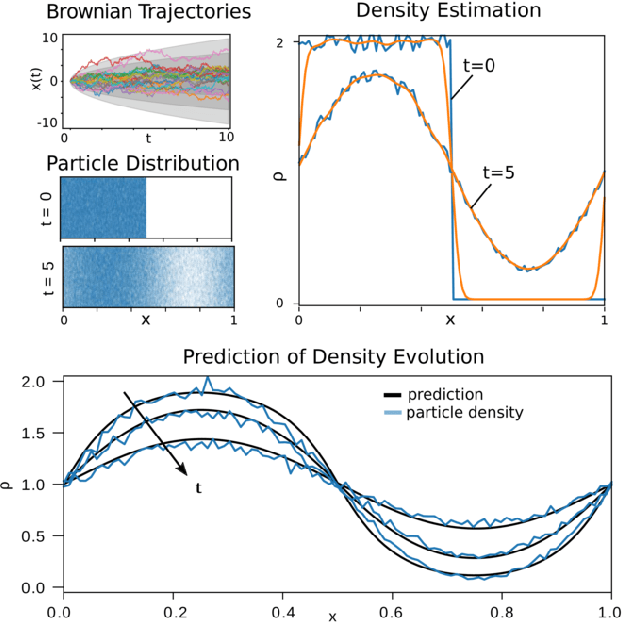
Data fields sampled on irregularly spaced points arise in many applications in the sciences and engineering. For regular grids, Convolutional Neural Networks (CNNs) have been successfully used to gaining benefits from weight sharing and invariances. We generalize CNNs by introducing methods for data on unstructured point clouds based on Generalized Moving Least Squares (GMLS). GMLS is a non-parametric technique for estimating linear bounded functionals from scattered data, and has recently been used in the literature for solving partial differential equations. By parameterizing the GMLS estimator, we obtain learning methods for operators with unstructured stencils. In GMLS-Nets the necessary calculations are local, readily parallelizable, and the estimator is supported by a rigorous approximation theory. We show how the framework may be used for unstructured physical data sets to perform functional regression to identify associated differential operators and to regress quantities of interest. The results suggest the architectures to be an attractive foundation for data-driven model development in scientific machine learning applications.

Importance of the Mathematical Foundations of Machine Learning Methods for Scientific and Engineering Applications

There has been a lot of recent interest in adopting machine learning methods for scientific and engineering applications. This has in large part been inspired by recent successes and advances in the domains of Natural Language Processing (NLP) and Image Classification (IC). However, scientific and engineering problems have their own unique characteristics and requirements raising new challenges for effective design and deployment of machine learning approaches. There is a strong need for further mathematical developments on the foundations of machine learning methods to increase the level of rigor of employed methods and to ensure more reliable and interpretable results. Also as reported in the recent literature on state-of-the-art results and indicated by the No Free Lunch Theorems of statistical learning theory incorporating some form of inductive bias and domain knowledge is essential to success. Consequently, even for existing and widely used methods there is a strong need for further mathematical work to facilitate ways to incorporate prior scientific knowledge and related inductive biases into learning frameworks and algorithms. We briefly discuss these topics and discuss some ideas proceeding in this direction.