Variational Autoencoders for Learning Nonlinear Dynamics of Physical Systems
Paper and Code
Dec 07, 2020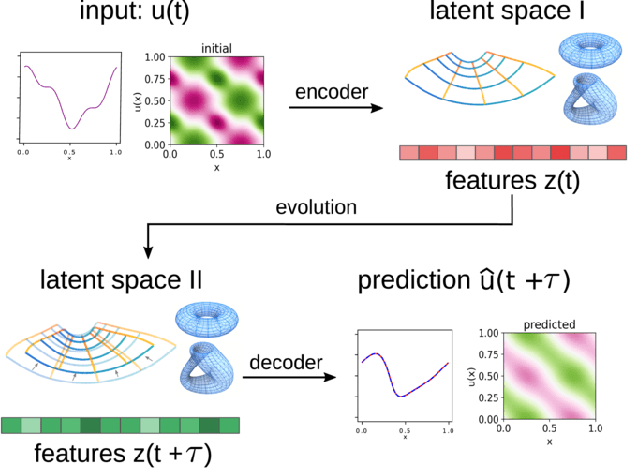
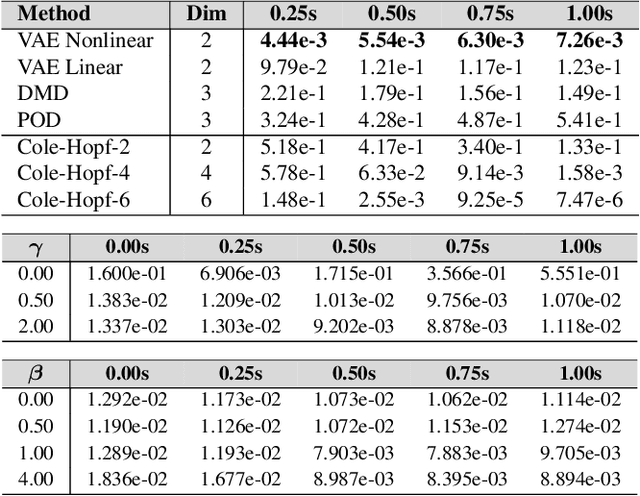

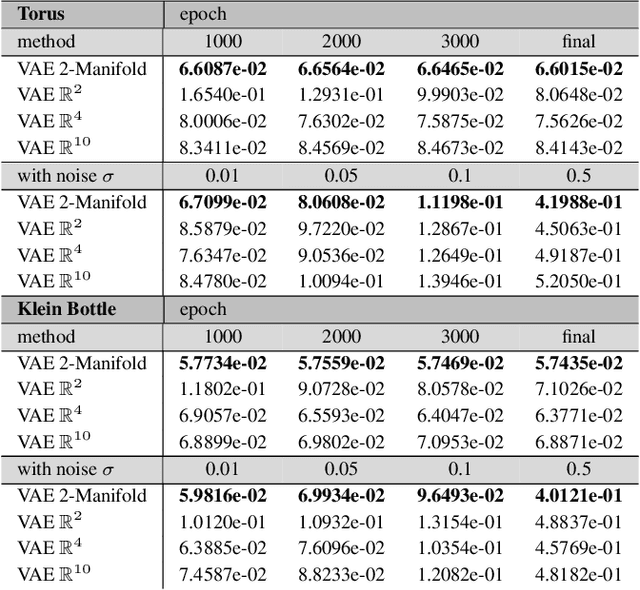
We develop data-driven methods for incorporating physical information for priors to learn parsimonious representations of nonlinear systems arising from parameterized PDEs and mechanics. Our approach is based on Variational Autoencoders (VAEs) for learning from observations nonlinear state space models. We develop ways to incorporate geometric and topological priors through general manifold latent space representations. We investigate the performance of our methods for learning low dimensional representations for the nonlinear Burgers equation and constrained mechanical systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge