Active learning for photonics

Active learning for photonic crystals explores the integration of analytic approximate Bayesian last layer neural networks (LL-BNNs) with uncertainty-driven sample selection to accelerate photonic band gap prediction. We employ an analytic LL-BNN formulation, corresponding to the infinite Monte Carlo sample limit, to obtain uncertainty estimates that are strongly correlated with the true predictive error on unlabeled candidate structures. These uncertainty scores drive an active learning strategy that prioritizes the most informative simulations during training. Applied to the task of predicting band gap sizes in two-dimensional, two-tone photonic crystals, our approach achieves up to a 2.6x reduction in required training data compared to a random sampling baseline while maintaining predictive accuracy. The efficiency gains arise from concentrating computational resources on high uncertainty regions of the design space rather than sampling uniformly. Given the substantial cost of full band structure simulations, especially in three dimensions, this data efficiency enables rapid and scalable surrogate modeling. Our results suggest that analytic LL-BNN based active learning can substantially accelerate topological optimization and inverse design workflows for photonic crystals, and more broadly, offers a general framework for data efficient regression across scientific machine learning domains.

GD-VAEs: Geometric Dynamic Variational Autoencoders for Learning Nonlinear Dynamics and Dimension Reductions

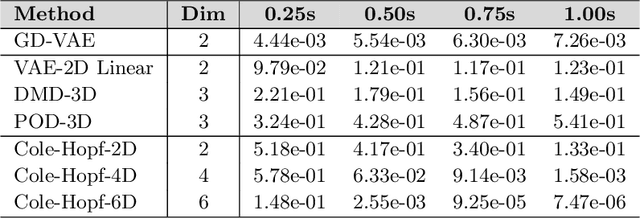
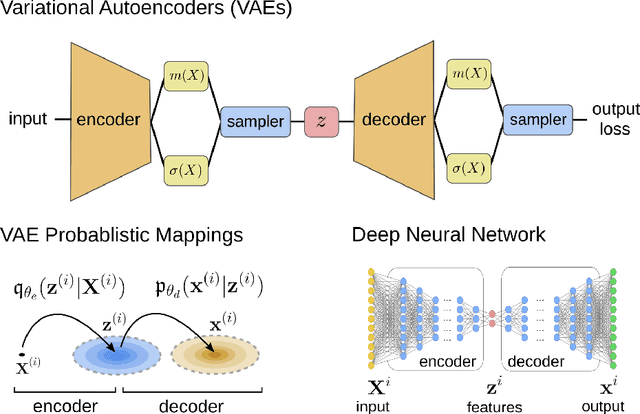
We develop data-driven methods incorporating geometric and topological information to learn parsimonious representations of nonlinear dynamics from observations. We develop approaches for learning nonlinear state space models of the dynamics for general manifold latent spaces using training strategies related to Variational Autoencoders (VAEs). Our methods are referred to as Geometric Dynamic (GD) Variational Autoencoders (GD-VAEs). We learn encoders and decoders for the system states and evolution based on deep neural network architectures that include general Multilayer Perceptrons (MLPs), Convolutional Neural Networks (CNNs), and Transpose CNNs (T-CNNs). Motivated by problems arising in parameterized PDEs and physics, we investigate the performance of our methods on tasks for learning low dimensional representations of the nonlinear Burgers equations, constrained mechanical systems, and spatial fields of reaction-diffusion systems. GD-VAEs provide methods for obtaining representations for use in learning tasks involving dynamics.

Variational Autoencoders for Learning Nonlinear Dynamics of Physical Systems

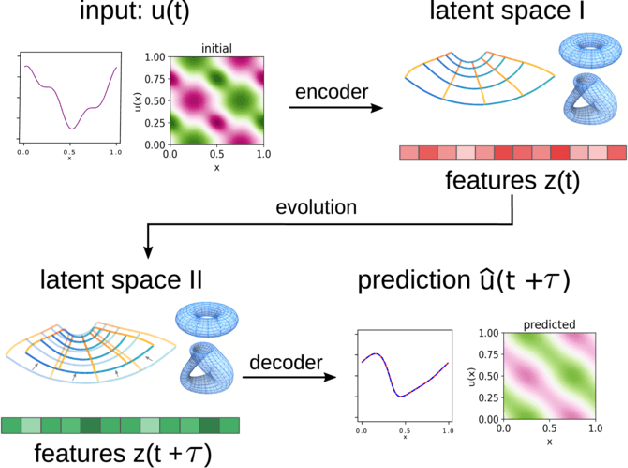
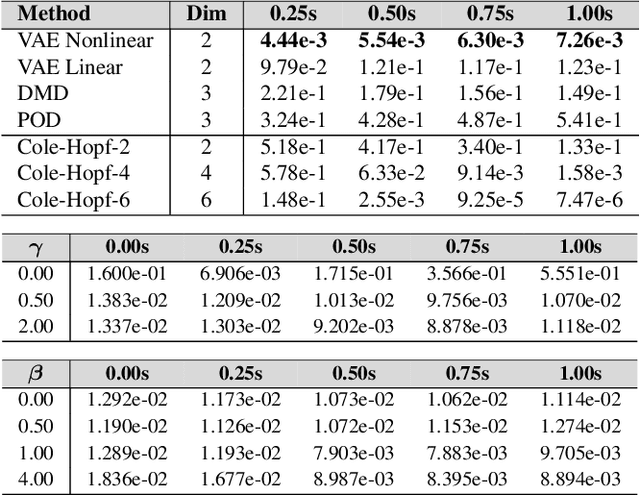
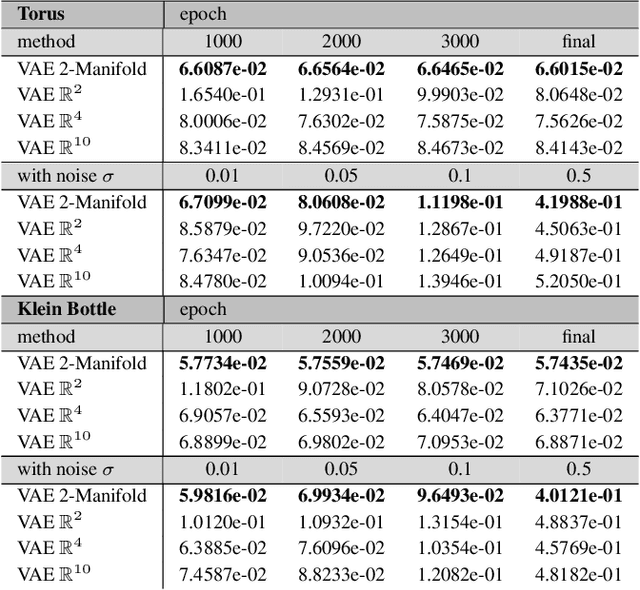
We develop data-driven methods for incorporating physical information for priors to learn parsimonious representations of nonlinear systems arising from parameterized PDEs and mechanics. Our approach is based on Variational Autoencoders (VAEs) for learning from observations nonlinear state space models. We develop ways to incorporate geometric and topological priors through general manifold latent space representations. We investigate the performance of our methods for learning low dimensional representations for the nonlinear Burgers equation and constrained mechanical systems.