Craig M. Hamel
Uncertainty quantification of neural network models of evolving processes via Langevin sampling
Apr 21, 2025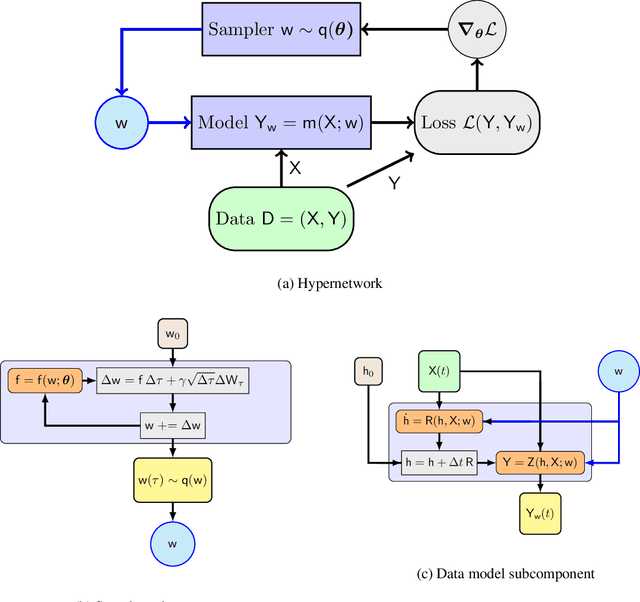
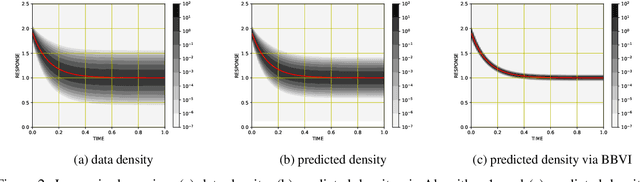
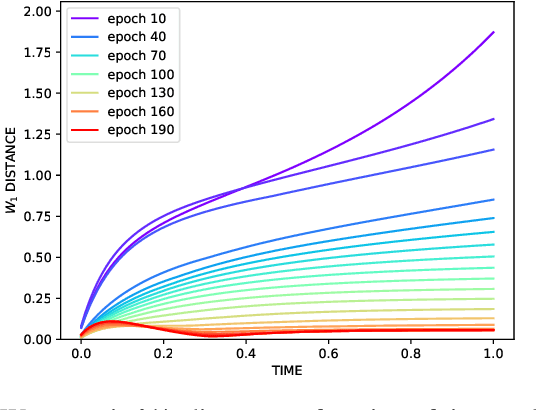
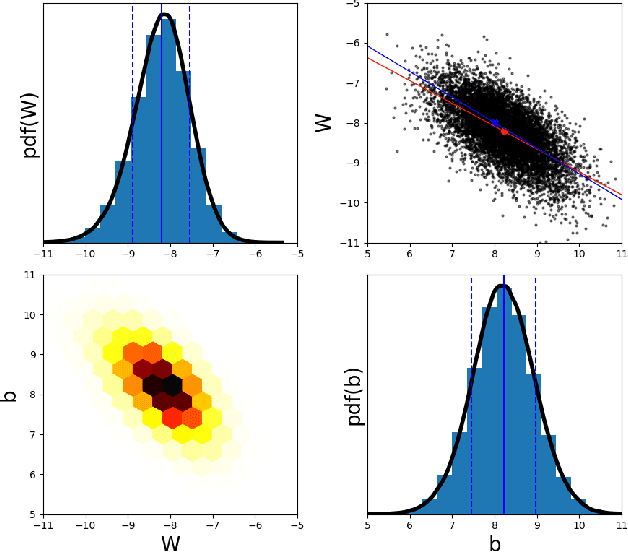
Abstract:We propose a scalable, approximate inference hypernetwork framework for a general model of history-dependent processes. The flexible data model is based on a neural ordinary differential equation (NODE) representing the evolution of internal states together with a trainable observation model subcomponent. The posterior distribution corresponding to the data model parameters (weights and biases) follows a stochastic differential equation with a drift term related to the score of the posterior that is learned jointly with the data model parameters. This Langevin sampling approach offers flexibility in balancing the computational budget between the evaluation cost of the data model and the approximation of the posterior density of its parameters. We demonstrate performance of the hypernetwork on chemical reaction and material physics data and compare it to mean-field variational inference.
Modular machine learning-based elastoplasticity: generalization in the context of limited data
Oct 15, 2022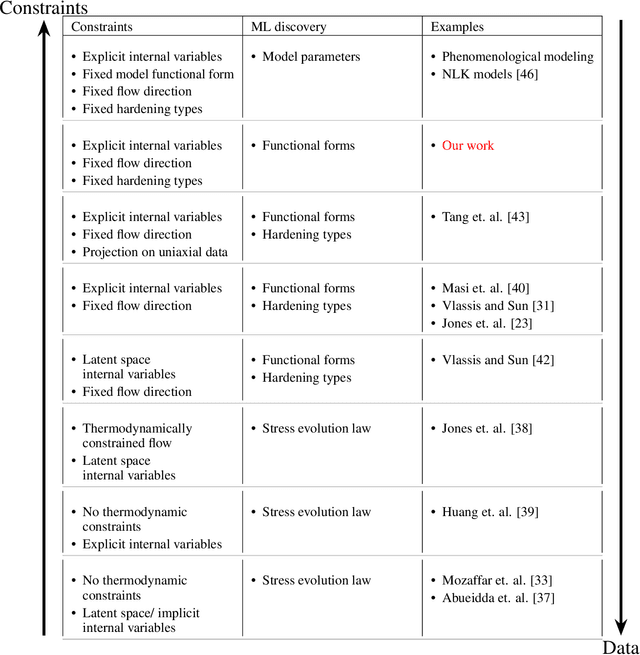
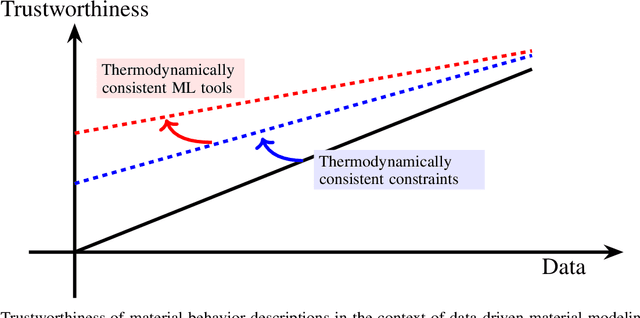
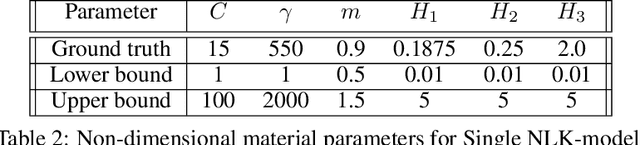
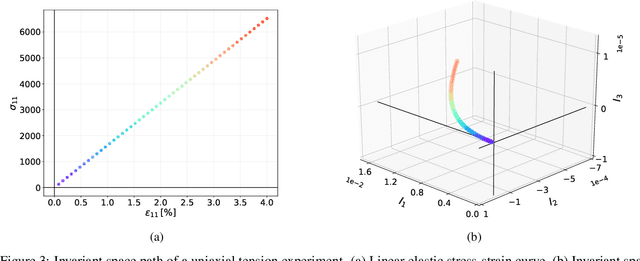
Abstract:The development of accurate constitutive models for materials that undergo path-dependent processes continues to be a complex challenge in computational solid mechanics. Challenges arise both in considering the appropriate model assumptions and from the viewpoint of data availability, verification, and validation. Recently, data-driven modeling approaches have been proposed that aim to establish stress-evolution laws that avoid user-chosen functional forms by relying on machine learning representations and algorithms. However, these approaches not only require a significant amount of data but also need data that probes the full stress space with a variety of complex loading paths. Furthermore, they rarely enforce all necessary thermodynamic principles as hard constraints. Hence, they are in particular not suitable for low-data or limited-data regimes, where the first arises from the cost of obtaining the data and the latter from the experimental limitations of obtaining labeled data, which is commonly the case in engineering applications. In this work, we discuss a hybrid framework that can work on a variable amount of data by relying on the modularity of the elastoplasticity formulation where each component of the model can be chosen to be either a classical phenomenological or a data-driven model depending on the amount of available information and the complexity of the response. The method is tested on synthetic uniaxial data coming from simulations as well as cyclic experimental data for structural materials. The discovered material models are found to not only interpolate well but also allow for accurate extrapolation in a thermodynamically consistent manner far outside the domain of the training data. Training aspects and details of the implementation of these models into Finite Element simulations are discussed and analyzed.
Calibrating constitutive models with full-field data via physics informed neural networks
Mar 30, 2022

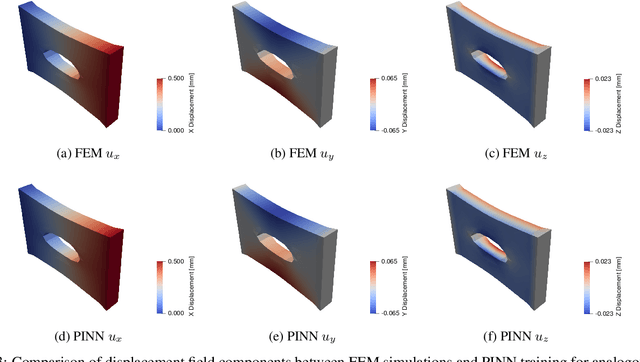

Abstract:The calibration of solid constitutive models with full-field experimental data is a long-standing challenge, especially in materials which undergo large deformation. In this paper, we propose a physics-informed deep-learning framework for the discovery of constitutive model parameterizations given full-field displacement data and global force-displacement data. Contrary to the majority of recent literature in this field, we work with the weak form of the governing equations rather than the strong form to impose physical constraints upon the neural network predictions. The approach presented in this paper is computationally efficient, suitable for irregular geometric domains, and readily ingests displacement data without the need for interpolation onto a computational grid. A selection of canonical hyperelastic materials models suitable for different material classes is considered including the Neo-Hookean, Gent, and Blatz-Ko constitutive models as exemplars for general hyperelastic behavior, polymer behavior with lock-up, and compressible foam behavior respectively. We demonstrate that physics informed machine learning is an enabling technology and may shift the paradigm of how full-field experimental data is utilized to calibrate constitutive models under finite deformations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge