Design of experiments for the calibration of history-dependent models via deep reinforcement learning and an enhanced Kalman filter

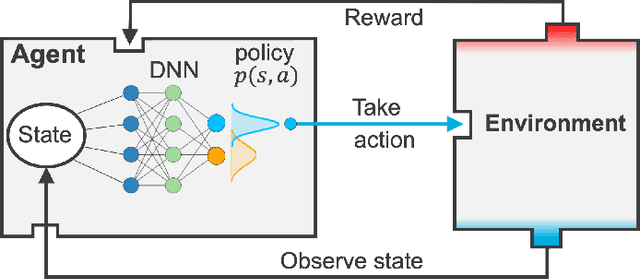
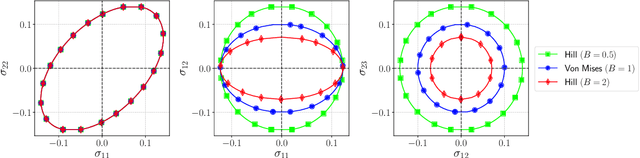
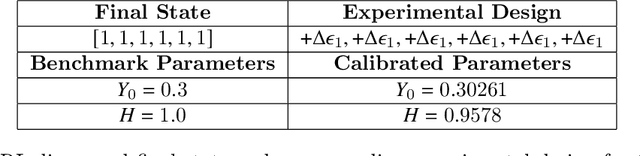
Experimental data is costly to obtain, which makes it difficult to calibrate complex models. For many models an experimental design that produces the best calibration given a limited experimental budget is not obvious. This paper introduces a deep reinforcement learning (RL) algorithm for design of experiments that maximizes the information gain measured by Kullback-Leibler (KL) divergence obtained via the Kalman filter (KF). This combination enables experimental design for rapid online experiments where traditional methods are too costly. We formulate possible configurations of experiments as a decision tree and a Markov decision process (MDP), where a finite choice of actions is available at each incremental step. Once an action is taken, a variety of measurements are used to update the state of the experiment. This new data leads to a Bayesian update of the parameters by the KF, which is used to enhance the state representation. In contrast to the Nash-Sutcliffe efficiency (NSE) index, which requires additional sampling to test hypotheses for forward predictions, the KF can lower the cost of experiments by directly estimating the values of new data acquired through additional actions. In this work our applications focus on mechanical testing of materials. Numerical experiments with complex, history-dependent models are used to verify the implementation and benchmark the performance of the RL-designed experiments.

Calibrating constitutive models with full-field data via physics informed neural networks

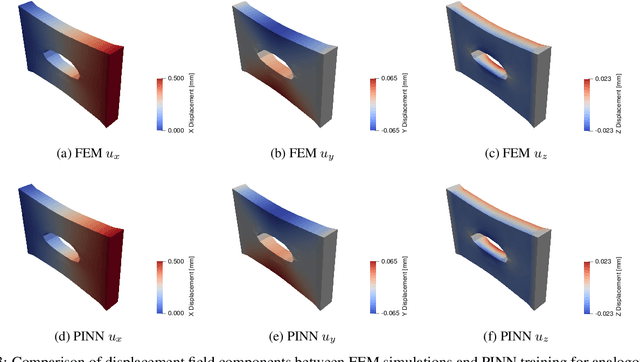
The calibration of solid constitutive models with full-field experimental data is a long-standing challenge, especially in materials which undergo large deformation. In this paper, we propose a physics-informed deep-learning framework for the discovery of constitutive model parameterizations given full-field displacement data and global force-displacement data. Contrary to the majority of recent literature in this field, we work with the weak form of the governing equations rather than the strong form to impose physical constraints upon the neural network predictions. The approach presented in this paper is computationally efficient, suitable for irregular geometric domains, and readily ingests displacement data without the need for interpolation onto a computational grid. A selection of canonical hyperelastic materials models suitable for different material classes is considered including the Neo-Hookean, Gent, and Blatz-Ko constitutive models as exemplars for general hyperelastic behavior, polymer behavior with lock-up, and compressible foam behavior respectively. We demonstrate that physics informed machine learning is an enabling technology and may shift the paradigm of how full-field experimental data is utilized to calibrate constitutive models under finite deformations.