Curvature in the Looking-Glass: Optimal Methods to Exploit Curvature of Expectation in the Loss Landscape

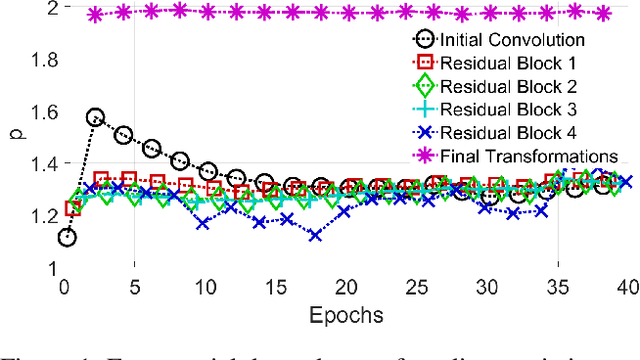
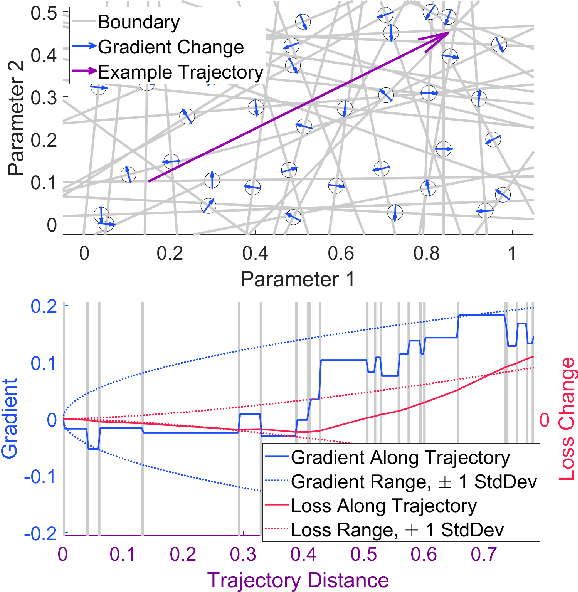
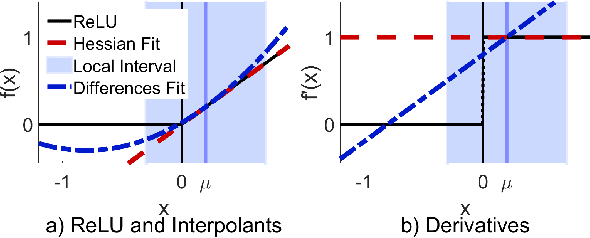
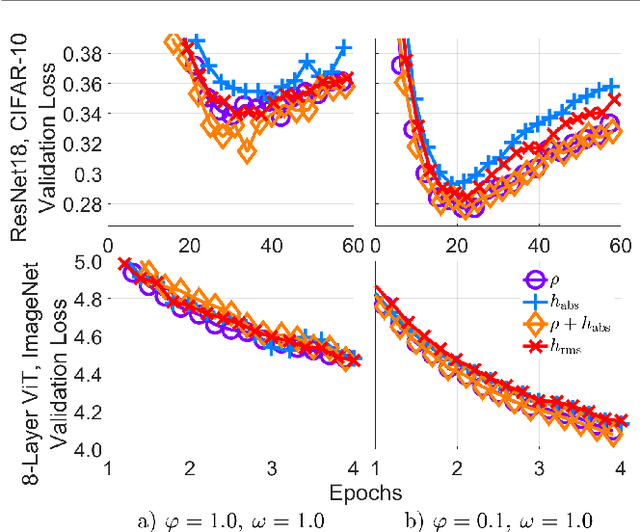
Harnessing the local topography of the loss landscape is a central challenge in advanced optimization tasks. By accounting for the effect of potential parameter changes, we can alter the model more efficiently. Contrary to standard assumptions, we find that the Hessian does not always approximate loss curvature well, particularly near gradient discontinuities, which commonly arise in deep learning architectures. We present a new conceptual framework to understand how curvature of expected changes in loss emerges in architectures with many rectified linear units. Each ReLU creates a parameter boundary that, when crossed, induces a pseudorandom gradient perturbation. Our derivations show how these discontinuities combine to form a glass-like structure, similar to amorphous solids that contain microscopic domains of strong, but random, atomic alignment. By estimating the density of the resulting gradient variations, we can bound how the loss may change with parameter movement. Our analysis includes the optimal kernel and sample distribution for approximating glass density from ordinary gradient evaluations. We also derive the optimal modification to quasi-Newton steps that incorporate both glass and Hessian terms, as well as certain exactness properties that are possible with Nesterov-accelerated gradient updates. Our algorithm, Alice, tests these techniques to determine which curvature terms are most impactful for training a given architecture and dataset. Additional safeguards enforce stable exploitation through step bounds that expand on the functionality of Adam. These theoretical and experimental tools lay groundwork to improve future efforts (e.g., pruning and quantization) by providing new insight into the loss landscape.

Metrics for Bayesian Optimal Experiment Design under Model Misspecification

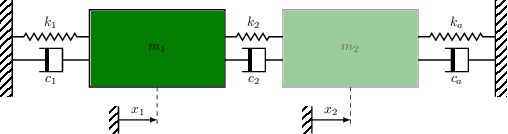
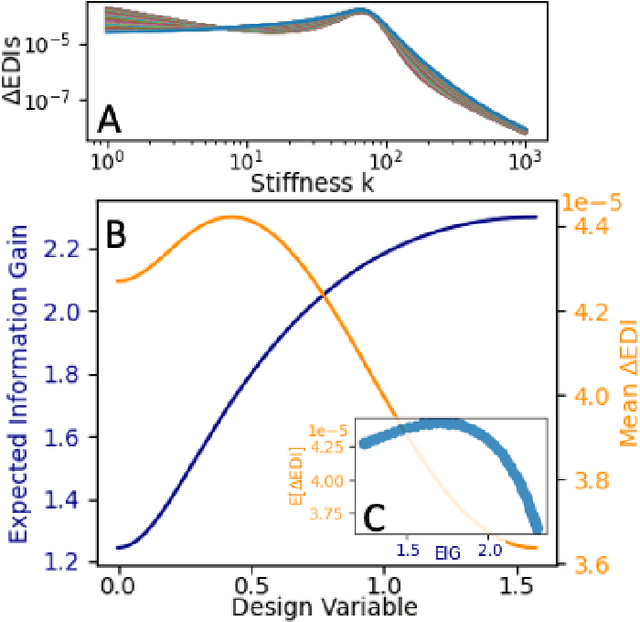
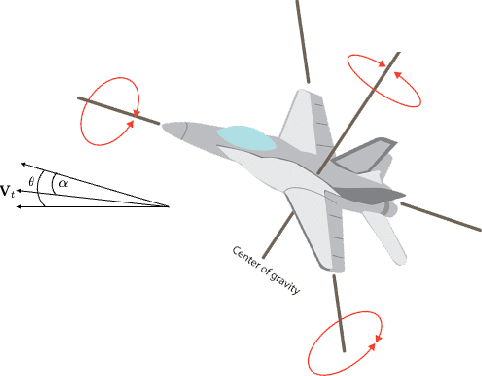
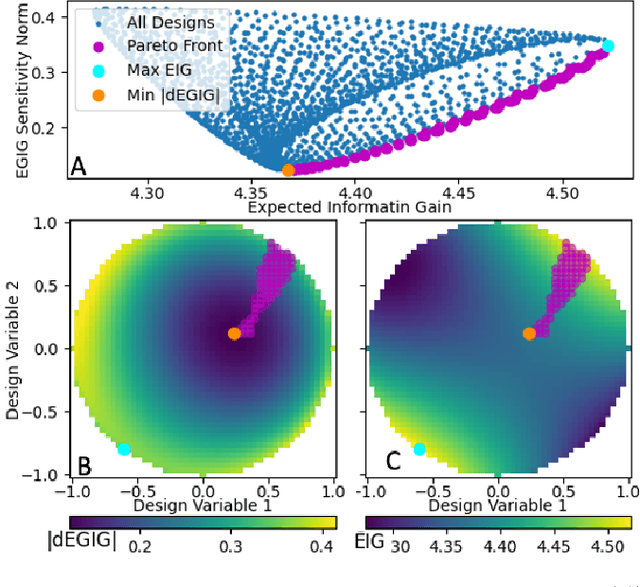
The conventional approach to Bayesian decision-theoretic experiment design involves searching over possible experiments to select a design that maximizes the expected value of a specified utility function. The expectation is over the joint distribution of all unknown variables implied by the statistical model that will be used to analyze the collected data. The utility function defines the objective of the experiment where a common utility function is the information gain. This article introduces an expanded framework for this process, where we go beyond the traditional Expected Information Gain criteria and introduce the Expected General Information Gain which measures robustness to the model discrepancy and Expected Discriminatory Information as a criterion to quantify how well an experiment can detect model discrepancy. The functionality of the framework is showcased through its application to a scenario involving a linearized spring mass damper system and an F-16 model where the model discrepancy is taken into account while doing Bayesian optimal experiment design.

Design of experiments for the calibration of history-dependent models via deep reinforcement learning and an enhanced Kalman filter

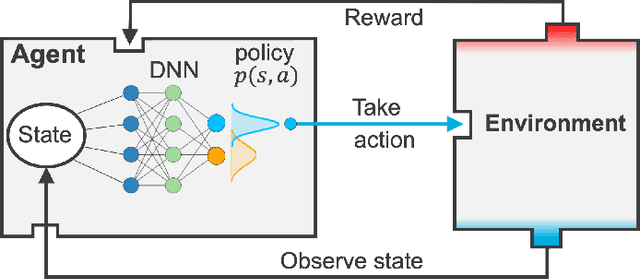
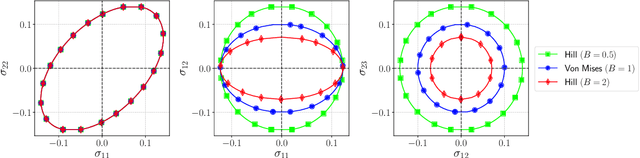
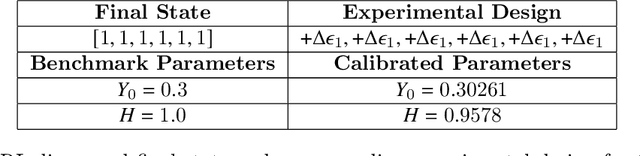
Experimental data is costly to obtain, which makes it difficult to calibrate complex models. For many models an experimental design that produces the best calibration given a limited experimental budget is not obvious. This paper introduces a deep reinforcement learning (RL) algorithm for design of experiments that maximizes the information gain measured by Kullback-Leibler (KL) divergence obtained via the Kalman filter (KF). This combination enables experimental design for rapid online experiments where traditional methods are too costly. We formulate possible configurations of experiments as a decision tree and a Markov decision process (MDP), where a finite choice of actions is available at each incremental step. Once an action is taken, a variety of measurements are used to update the state of the experiment. This new data leads to a Bayesian update of the parameters by the KF, which is used to enhance the state representation. In contrast to the Nash-Sutcliffe efficiency (NSE) index, which requires additional sampling to test hypotheses for forward predictions, the KF can lower the cost of experiments by directly estimating the values of new data acquired through additional actions. In this work our applications focus on mechanical testing of materials. Numerical experiments with complex, history-dependent models are used to verify the implementation and benchmark the performance of the RL-designed experiments.