Smart Portable Computer

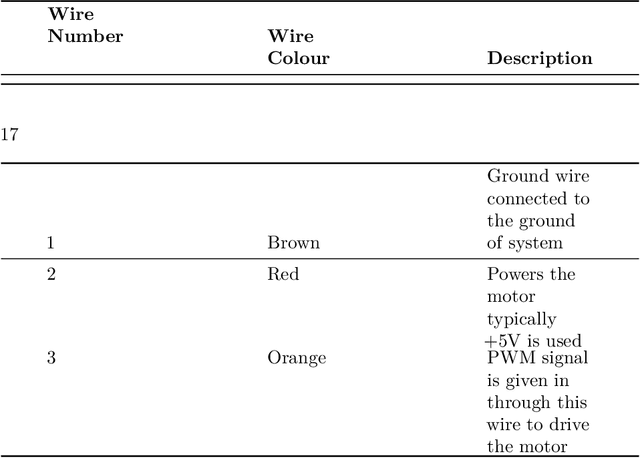
Amidst the COVID-19 pandemic, with many organizations, schools, colleges, and universities transitioning to virtual platforms, students encountered difficulties in acquiring PCs such as desktops or laptops. The starting prices, around 15,000 INR, often failed to offer adequate system specifications, posing a challenge for consumers. Additionally, those reliant on laptops for work found the conventional approach cumbersome. Enter the "Portable Smart Computer," a leap into the future of computing. This innovative device boasts speed and performance comparable to traditional desktops but in a compact, energy-efficient, and cost-effective package. It delivers a seamless desktop experience, whether one is editing documents, browsing multiple tabs, managing spreadsheets, or creating presentations. Moreover, it supports programming languages like Python, C, C++, as well as compilers such as Keil and Xilinx, catering to the needs of programmers.

Metrics for Bayesian Optimal Experiment Design under Model Misspecification

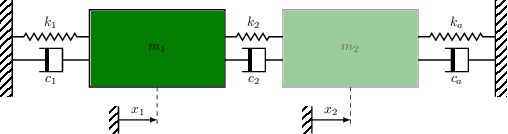
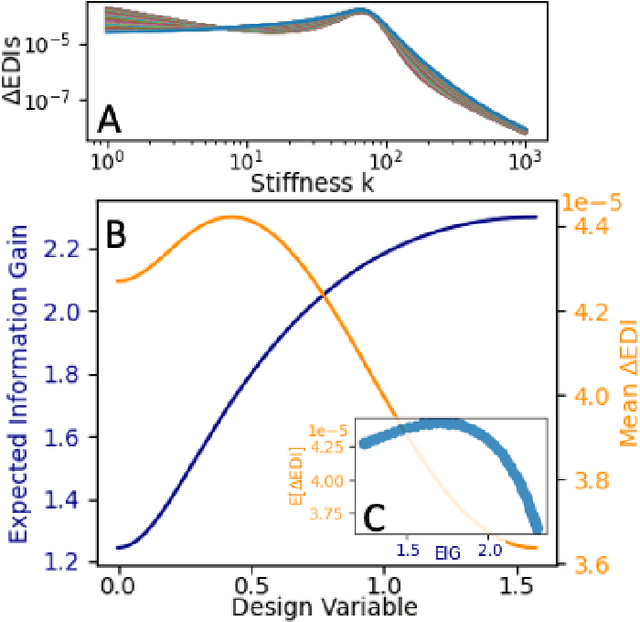
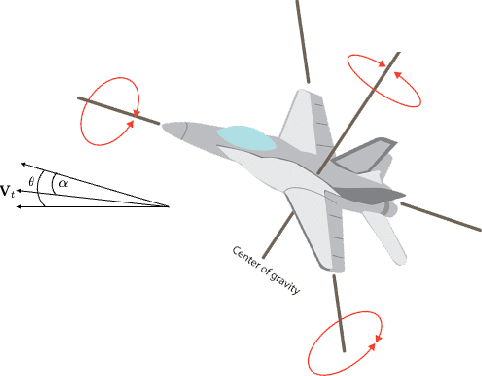
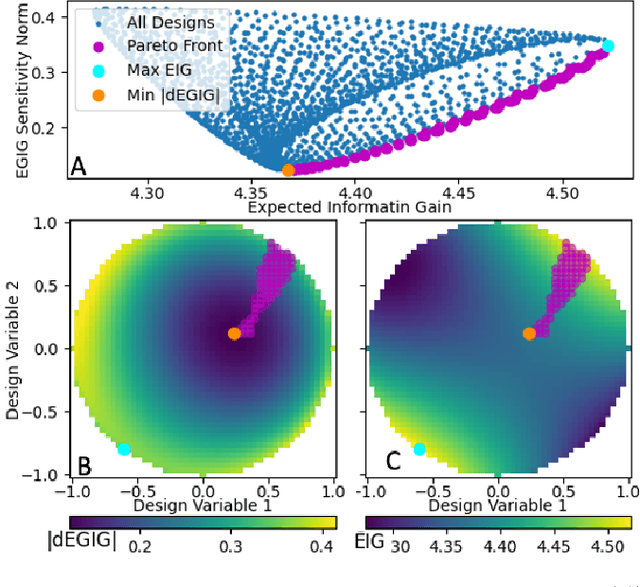
The conventional approach to Bayesian decision-theoretic experiment design involves searching over possible experiments to select a design that maximizes the expected value of a specified utility function. The expectation is over the joint distribution of all unknown variables implied by the statistical model that will be used to analyze the collected data. The utility function defines the objective of the experiment where a common utility function is the information gain. This article introduces an expanded framework for this process, where we go beyond the traditional Expected Information Gain criteria and introduce the Expected General Information Gain which measures robustness to the model discrepancy and Expected Discriminatory Information as a criterion to quantify how well an experiment can detect model discrepancy. The functionality of the framework is showcased through its application to a scenario involving a linearized spring mass damper system and an F-16 model where the model discrepancy is taken into account while doing Bayesian optimal experiment design.

Variational Kalman Filtering with Hinf-Based Correction for Robust Bayesian Learning in High Dimensions

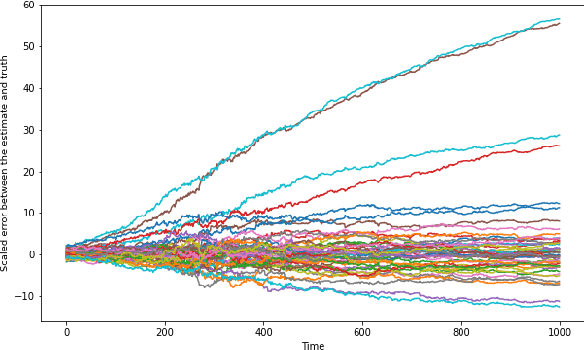
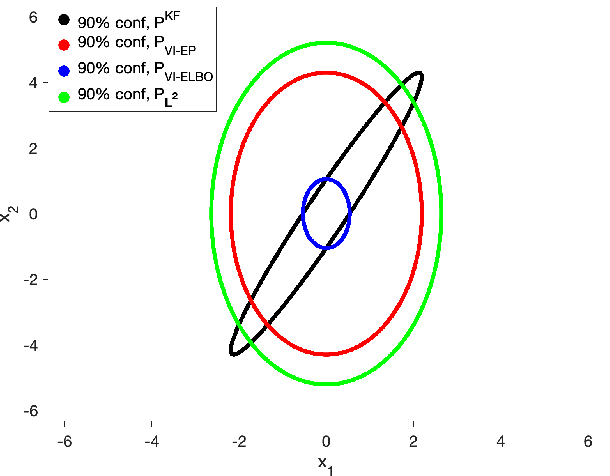
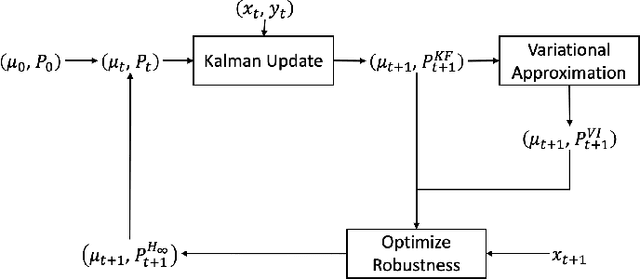
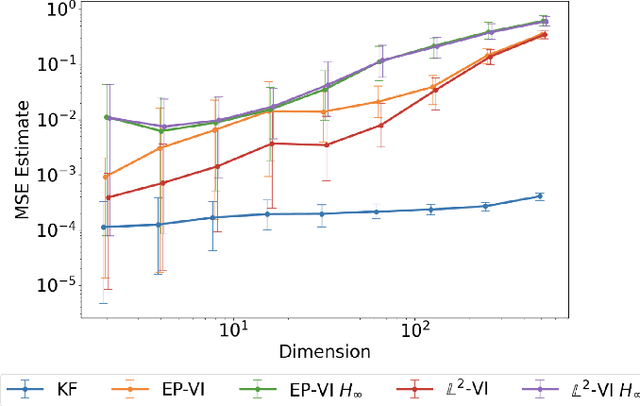
In this paper, we address the problem of convergence of sequential variational inference filter (VIF) through the application of a robust variational objective and Hinf-norm based correction for a linear Gaussian system. As the dimension of state or parameter space grows, performing the full Kalman update with the dense covariance matrix for a large scale system requires increased storage and computational complexity, making it impractical. The VIF approach, based on mean-field Gaussian variational inference, reduces this burden through the variational approximation to the covariance usually in the form of a diagonal covariance approximation. The challenge is to retain convergence and correct for biases introduced by the sequential VIF steps. We desire a framework that improves feasibility while still maintaining reasonable proximity to the optimal Kalman filter as data is assimilated. To accomplish this goal, a Hinf-norm based optimization perturbs the VIF covariance matrix to improve robustness. This yields a novel VIF- Hinf recursion that employs consecutive variational inference and Hinf based optimization steps. We explore the development of this method and investigate a numerical example to illustrate the effectiveness of the proposed filter.

Adaptive n-ary Activation Functions for Probabilistic Boolean Logic

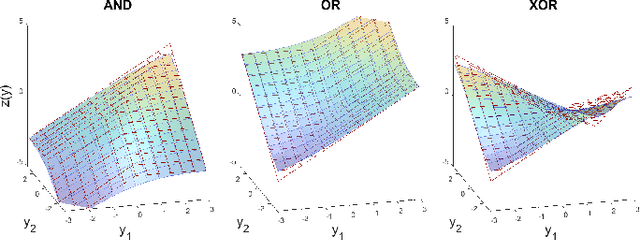
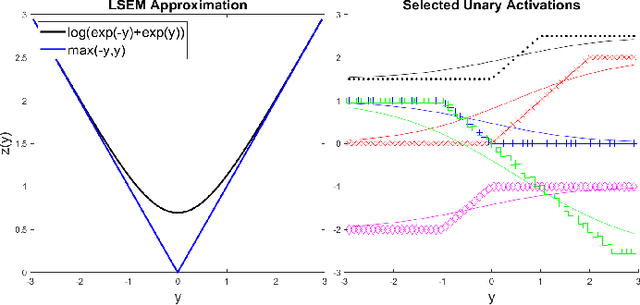
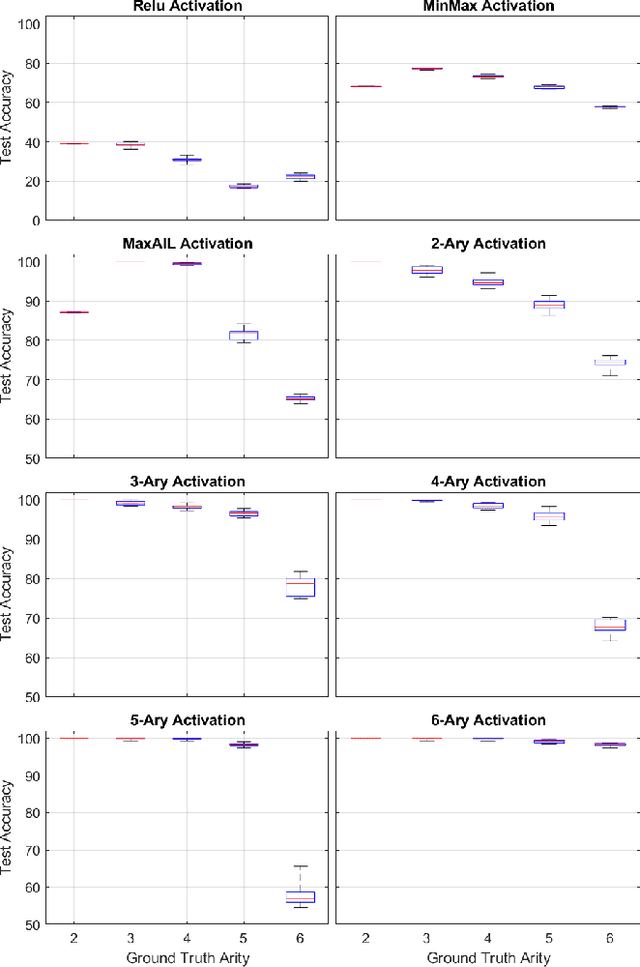
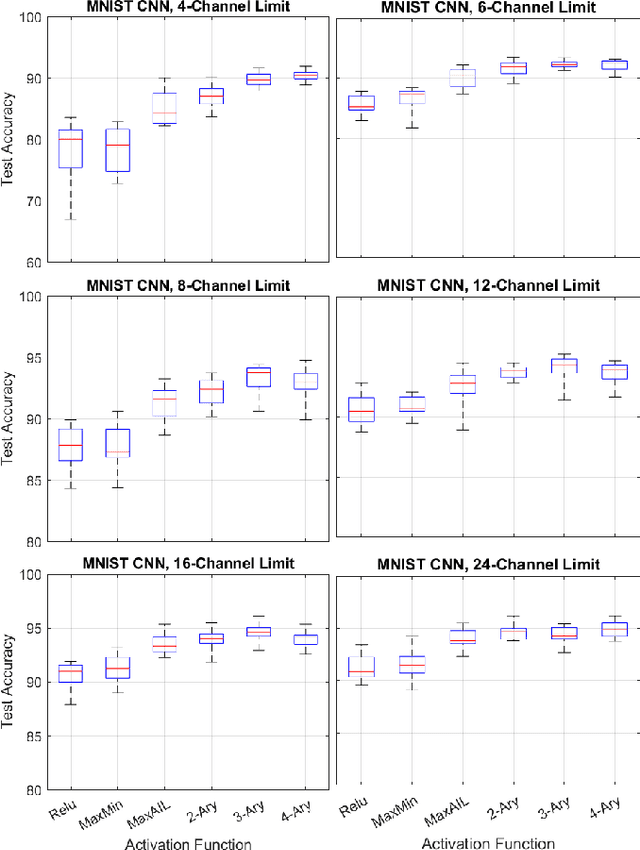
Balancing model complexity against the information contained in observed data is the central challenge to learning. In order for complexity-efficient models to exist and be discoverable in high dimensions, we require a computational framework that relates a credible notion of complexity to simple parameter representations. Further, this framework must allow excess complexity to be gradually removed via gradient-based optimization. Our n-ary, or n-argument, activation functions fill this gap by approximating belief functions (probabilistic Boolean logic) using logit representations of probability. Just as Boolean logic determines the truth of a consequent claim from relationships among a set of antecedent propositions, probabilistic formulations generalize predictions when antecedents, truth tables, and consequents all retain uncertainty. Our activation functions demonstrate the ability to learn arbitrary logic, such as the binary exclusive disjunction (p xor q) and ternary conditioned disjunction ( c ? p : q ), in a single layer using an activation function of matching or greater arity. Further, we represent belief tables using a basis that directly associates the number of nonzero parameters to the effective arity of the belief function, thus capturing a concrete relationship between logical complexity and efficient parameter representations. This opens optimization approaches to reduce logical complexity by inducing parameter sparsity.

Optimal Sensor Precision for Multi-Rate Sensing for Bounded Estimation Error

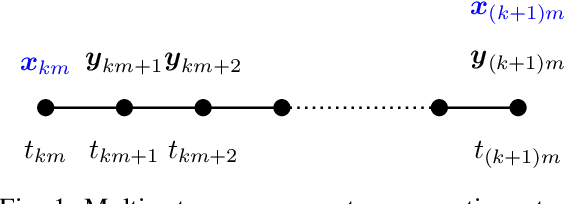
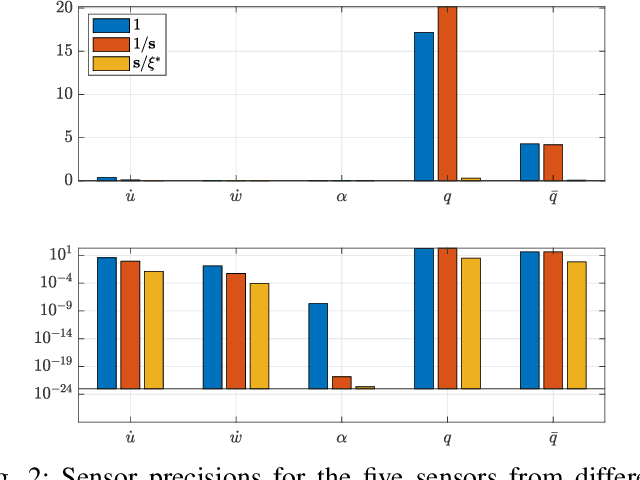
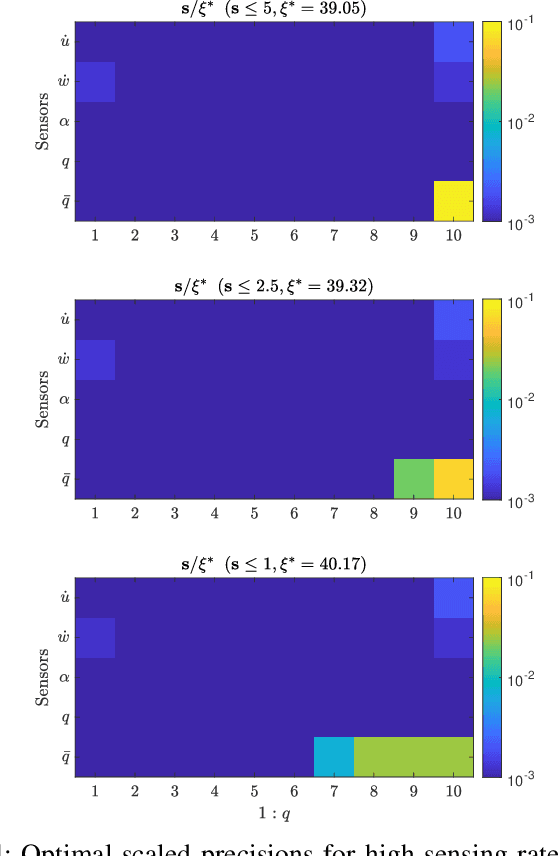
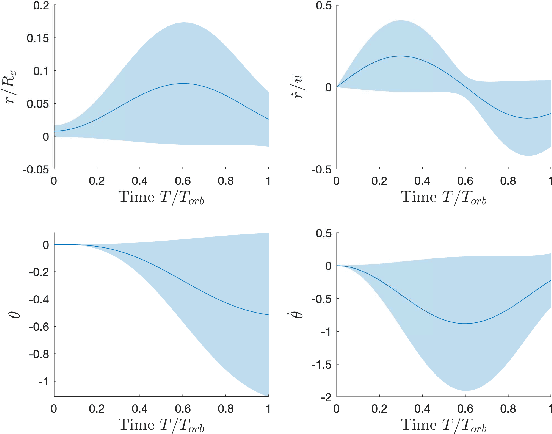
We address the problem of determining optimal sensor precisions for estimating the states of linear time-varying discrete-time stochastic dynamical systems, with guaranteed bounds on the estimation errors. This is performed in the Kalman filtering framework, where the sensor precisions are treated as variables. They are determined by solving a constrained convex optimization problem, which guarantees the specified upper bound on the posterior error variance. Optimal sensor precisions are determined by minimizing the l1 norm, which promotes sparseness in the solution and indirectly addresses the sensor selection problem. The theory is applied to realistic flight mechanics and astrodynamics problems to highlight its engineering value. These examples demonstrate the application of the presented theory to a) determine redundant sensing architectures for linear time invariant systems, b) accurately estimate states with low-cost sensors, and c) optimally schedule sensors for linear time-varying systems.