Privacy-aware Gaussian Process Regression

We propose the first theoretical and methodological framework for Gaussian process regression subject to privacy constraints. The proposed method can be used when a data owner is unwilling to share a high-fidelity supervised learning model built from their data with the public due to privacy concerns. The key idea of the proposed method is to add synthetic noise to the data until the predictive variance of the Gaussian process model reaches a prespecified privacy level. The optimal covariance matrix of the synthetic noise is formulated in terms of semi-definite programming. We also introduce the formulation of privacy-aware solutions under continuous privacy constraints using kernel-based approaches, and study their theoretical properties. The proposed method is illustrated by considering a model that tracks the trajectories of satellites.

Optimal Sensor Precision for Multi-Rate Sensing for Bounded Estimation Error

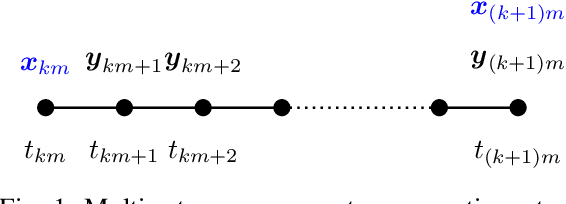
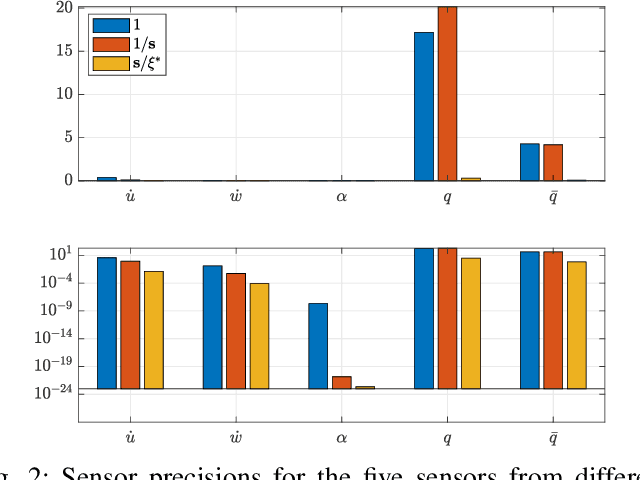
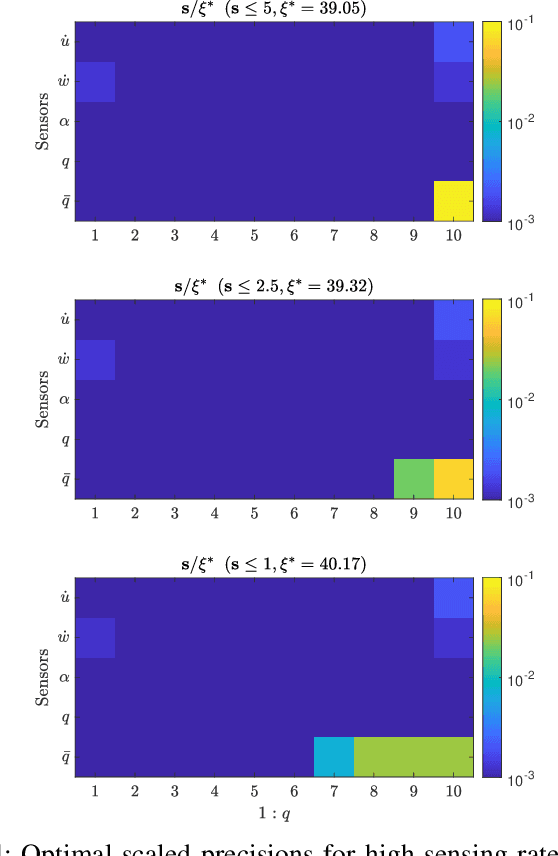
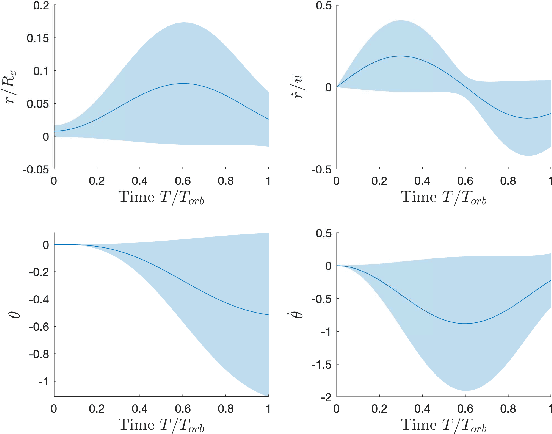
We address the problem of determining optimal sensor precisions for estimating the states of linear time-varying discrete-time stochastic dynamical systems, with guaranteed bounds on the estimation errors. This is performed in the Kalman filtering framework, where the sensor precisions are treated as variables. They are determined by solving a constrained convex optimization problem, which guarantees the specified upper bound on the posterior error variance. Optimal sensor precisions are determined by minimizing the l1 norm, which promotes sparseness in the solution and indirectly addresses the sensor selection problem. The theory is applied to realistic flight mechanics and astrodynamics problems to highlight its engineering value. These examples demonstrate the application of the presented theory to a) determine redundant sensing architectures for linear time invariant systems, b) accurately estimate states with low-cost sensors, and c) optimally schedule sensors for linear time-varying systems.

Optimal Transport Based Refinement of Physics-Informed Neural Networks

In this paper, we propose a refinement strategy to the well-known Physics-Informed Neural Networks (PINNs) for solving partial differential equations (PDEs) based on the concept of Optimal Transport (OT). Conventional black-box PINNs solvers have been found to suffer from a host of issues: spectral bias in fully-connected architectures, unstable gradient pathologies, as well as difficulties with convergence and accuracy. Current network training strategies are agnostic to dimension sizes and rely on the availability of powerful computing resources to optimize through a large number of collocation points. This is particularly challenging when studying stochastic dynamical systems with the Fokker-Planck-Kolmogorov Equation (FPKE), a second-order PDE which is typically solved in high-dimensional state space. While we focus exclusively on the stationary form of the FPKE, positivity and normalization constraints on its solution make it all the more unfavorable to solve directly using standard PINNs approaches. To mitigate the above challenges, we present a novel training strategy for solving the FPKE using OT-based sampling to supplement the existing PINNs framework. It is an iterative approach that induces a network trained on a small dataset to add samples to its training dataset from regions where it nominally makes the most error. The new samples are found by solving a linear programming problem at every iteration. The paper is complemented by an experimental evaluation of the proposed method showing its applicability on a variety of stochastic systems with nonlinear dynamics.