Aggregation Models with Optimal Weights for Distributed Gaussian Processes

Gaussian process (GP) models have received increasingly attentions in recent years due to their superb prediction accuracy and modeling flexibility. To address the computational burdens of GP models for large-scale datasets, distributed learning for GPs are often adopted. Current aggregation models for distributed GPs are not time-efficient when incorporating correlations between GP experts. In this work, we propose a novel approach for aggregated prediction in distributed GPs. The technique is suitable for both the exact and sparse variational GPs. The proposed method incorporates correlations among experts, leading to better prediction accuracy with manageable computational requirements. As demonstrated by empirical studies, the proposed approach results in more stable predictions in less time than state-of-the-art consistent aggregation models.

Gaussian Processes Sampling with Sparse Grids under Additive Schwarz Preconditioner

Gaussian processes (GPs) are widely used in non-parametric Bayesian modeling, and play an important role in various statistical and machine learning applications. In a variety tasks of uncertainty quantification, generating random sample paths of GPs is of interest. As GP sampling requires generating high-dimensional Gaussian random vectors, it is computationally challenging if a direct method, such as the Cholesky decomposition, is used. In this paper, we propose a scalable algorithm for sampling random realizations of the prior and posterior of GP models. The proposed algorithm leverages inducing points approximation with sparse grids, as well as additive Schwarz preconditioners, which reduce computational complexity, and ensure fast convergence. We demonstrate the efficacy and accuracy of the proposed method through a series of experiments and comparisons with other recent works.

A General Theory for Kernel Packets: from state space model to compactly supported basis

It is well known that the state space (SS) model formulation of a Gaussian process (GP) can lower its training and prediction time both to O(n) for n data points. We prove that an $m$-dimensional SS model formulation of GP is equivalent to a concept we introduce as the general right Kernel Packet (KP): a transformation for the GP covariance function $K$ such that $\sum_{i=0}^{m}a_iD_t^{(j)}K(t,t_i)=0$ holds for any $t \leq t_1$, 0 $\leq j \leq m-1$, and $m+1$ consecutive points $t_i$, where ${D}_t^{(j)}f(t) $ denotes $j$-th order derivative acting on $t$. We extend this idea to the backward SS model formulation of the GP, leading to the concept of the left KP for next $m$ consecutive points: $\sum_{i=0}^{m}b_i{D}_t^{(j)}K(t,t_{m+i})=0$ for any $t\geq t_{2m}$. By combining both left and right KPs, we can prove that a suitable linear combination of these covariance functions yields $m$ compactly supported KP functions: $\phi^{(j)}(t)=0$ for any $t\not\in(t_0,t_{2m})$ and $j=0,\cdots,m-1$. KPs further reduce the prediction time of GP to O(log n) or even O(1), can be applied to more general problems involving the derivative of GPs, and have multi-dimensional generalization for scattered data.

Privacy-aware Gaussian Process Regression

We propose the first theoretical and methodological framework for Gaussian process regression subject to privacy constraints. The proposed method can be used when a data owner is unwilling to share a high-fidelity supervised learning model built from their data with the public due to privacy concerns. The key idea of the proposed method is to add synthetic noise to the data until the predictive variance of the Gaussian process model reaches a prespecified privacy level. The optimal covariance matrix of the synthetic noise is formulated in terms of semi-definite programming. We also introduce the formulation of privacy-aware solutions under continuous privacy constraints using kernel-based approaches, and study their theoretical properties. The proposed method is illustrated by considering a model that tracks the trajectories of satellites.

Renewing Iterative Self-labeling Domain Adaptation with Application to the Spine Motion Prediction

The area of transfer learning comprises supervised machine learning methods that cope with the issue when the training and testing data have different input feature spaces or distributions. In this work, we propose a novel transfer learning algorithm called Renewing Iterative Self-labeling Domain Adaptation (Re-ISDA). In this work, we propose a novel transfer learning algorithm called Renewing Iterative Self-labeling Domain Adaptation (Re-ISDA).

Kernel Packet: An Exact and Scalable Algorithm for Gaussian Process Regression with Matérn Correlations

We develop an exact and scalable algorithm for one-dimensional Gaussian process regression with Mat\'ern correlations whose smoothness parameter $\nu$ is a half-integer. The proposed algorithm only requires $\mathcal{O}(\nu^3 n)$ operations and $\mathcal{O}(\nu n)$ storage. This leads to a linear-cost solver since $\nu$ is chosen to be fixed and usually very small in most applications. The proposed method can be applied to multi-dimensional problems if a full grid or a sparse grid design is used. The proposed method is based on a novel theory for Mat\'ern correlation functions. We find that a suitable rearrangement of these correlation functions can produce a compactly supported function, called a "kernel packet". Using a set of kernel packets as basis functions leads to a sparse representation of the covariance matrix that results in the proposed algorithm. Simulation studies show that the proposed algorithm, when applicable, is significantly superior to the existing alternatives in both the computational time and predictive accuracy.

A Sparse Expansion For Deep Gaussian Processes

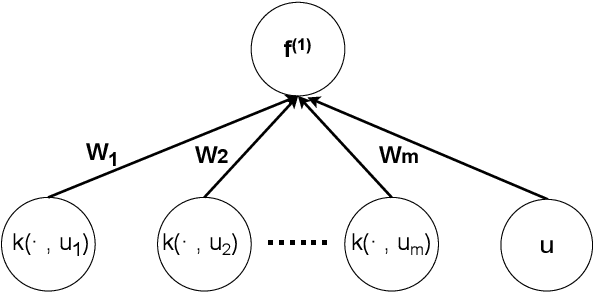
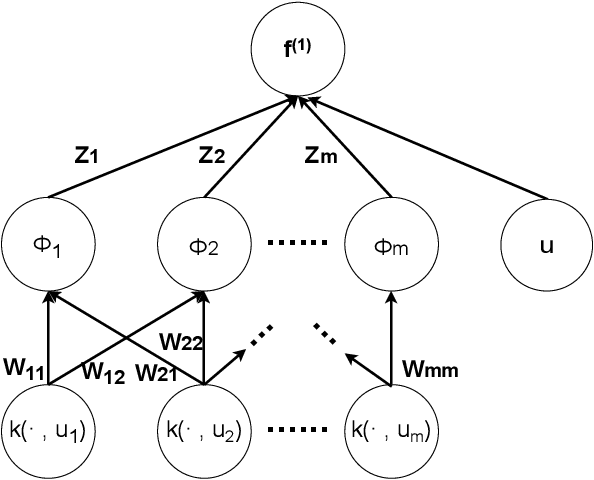
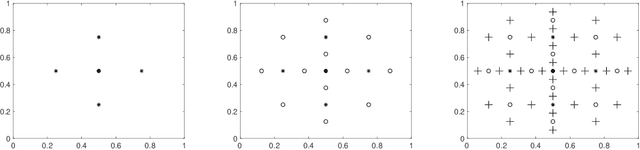
Deep Gaussian Processes (DGP) enable a non-parametric approach to quantify the uncertainty of complex deep machine learning models. Conventional inferential methods for DGP models can suffer from high computational complexity as they require large-scale operations with kernel matrices for training and inference. In this work, we propose an efficient scheme for accurate inference and prediction based on a range of Gaussian Processes, called the Tensor Markov Gaussian Processes (TMGP). We construct an induced approximation of TMGP referred to as the hierarchical expansion. Next, we develop a deep TMGP (DTMGP) model as the composition of multiple hierarchical expansion of TMGPs. The proposed DTMGP model has the following properties: (1) the outputs of each activation function are deterministic while the weights are chosen independently from standard Gaussian distribution; (2) in training or prediction, only O(polylog(M)) (out of M) activation functions have non-zero outputs, which significantly boosts the computational efficiency. Our numerical experiments on real datasets show the superior computational efficiency of DTMGP versus other DGP models.

High-Dimensional Simulation Optimization via Brownian Fields and Sparse Grids

High-dimensional simulation optimization is notoriously challenging. We propose a new sampling algorithm that converges to a global optimal solution and suffers minimally from the curse of dimensionality. The algorithm consists of two stages. First, we take samples following a sparse grid experimental design and approximate the response surface via kernel ridge regression with a Brownian field kernel. Second, we follow the expected improvement strategy -- with critical modifications that boost the algorithm's sample efficiency -- to iteratively sample from the next level of the sparse grid. Under mild conditions on the smoothness of the response surface and the simulation noise, we establish upper bounds on the convergence rate for both noise-free and noisy simulation samples. These upper bounds deteriorate only slightly in the dimension of the feasible set, and they can be improved if the objective function is known to be of a higher-order smoothness. Extensive numerical experiments demonstrate that the proposed algorithm dramatically outperforms typical alternatives in practice.

The temporal overfitting problem with applications in wind power curve modeling

This paper is concerned with a nonparametric regression problem in which the independence assumption of the input variables and the residuals is no longer valid. Using existing model selection methods, like cross validation, the presence of temporal autocorrelation in the input variables and the error terms leads to model overfitting. This phenomenon is referred to as temporal overfitting, which causes loss of performance while predicting responses for a time domain different from the training time domain. We propose a new method to tackle the temporal overfitting problem. Our nonparametric model is partitioned into two parts -- a time-invariant component and a time-varying component, each of which is modeled through a Gaussian process regression. The key in our inference is a thinning-based strategy, an idea borrowed from Markov chain Monte Carlo sampling, to estimate the two components, respectively. Our specific application in this paper targets the power curve modeling in wind energy. In our numerical studies, we compare extensively our proposed method with both existing power curve models and available ideas for handling temporal overfitting. Our approach yields significant improvement in prediction both in and outside the time domain covered by the training data.

Overcoming the Curse of Dimensionality in Density Estimation with Mixed Sobolev GANs

We propose a novel GAN framework for non-parametric density estimation with high-dimensional data. This framework is based on a novel density estimator, called the hyperbolic cross density estimator, which enjoys nice convergence properties in the mixed Sobolev spaces. As modifications of the usual Sobolev spaces, the mixed Sobolev spaces are more suitable for describing high-dimensional density functions. We prove that, unlike other existing approaches, the proposed GAN framework does not suffer the curse of dimensionality and can achieve the optimal convergence rate of $O_p(n^{-1/2})$, with $n$ data points in an arbitrary fixed dimension. We also study the universality of GANs in terms of the existence of ReLU networks which can approximate the density functions in the mixed Sobolev spaces up to any accuracy level.