Variational Kalman Filtering with Hinf-Based Correction for Robust Bayesian Learning in High Dimensions

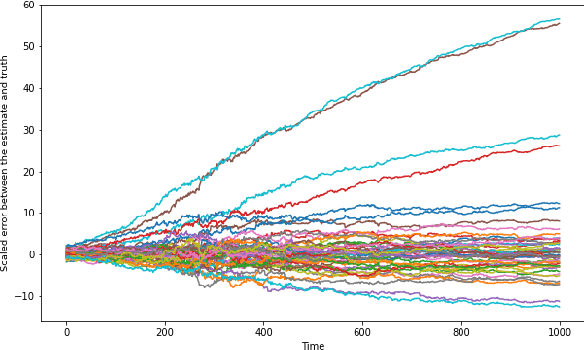
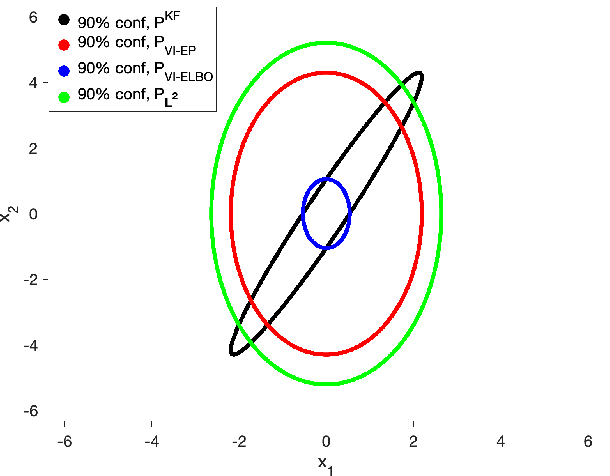
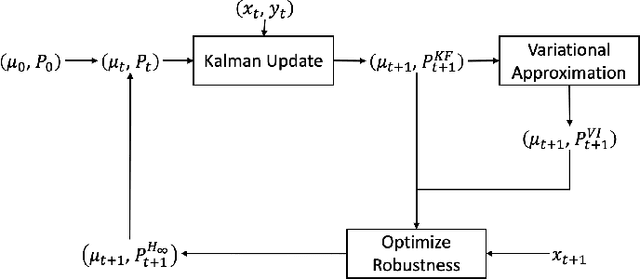
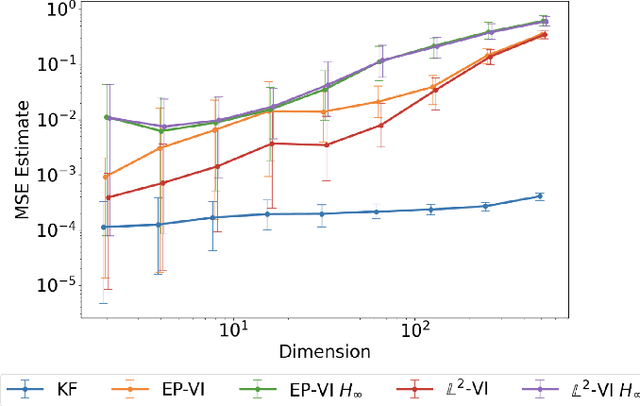
In this paper, we address the problem of convergence of sequential variational inference filter (VIF) through the application of a robust variational objective and Hinf-norm based correction for a linear Gaussian system. As the dimension of state or parameter space grows, performing the full Kalman update with the dense covariance matrix for a large scale system requires increased storage and computational complexity, making it impractical. The VIF approach, based on mean-field Gaussian variational inference, reduces this burden through the variational approximation to the covariance usually in the form of a diagonal covariance approximation. The challenge is to retain convergence and correct for biases introduced by the sequential VIF steps. We desire a framework that improves feasibility while still maintaining reasonable proximity to the optimal Kalman filter as data is assimilated. To accomplish this goal, a Hinf-norm based optimization perturbs the VIF covariance matrix to improve robustness. This yields a novel VIF- Hinf recursion that employs consecutive variational inference and Hinf based optimization steps. We explore the development of this method and investigate a numerical example to illustrate the effectiveness of the proposed filter.

Adaptive n-ary Activation Functions for Probabilistic Boolean Logic

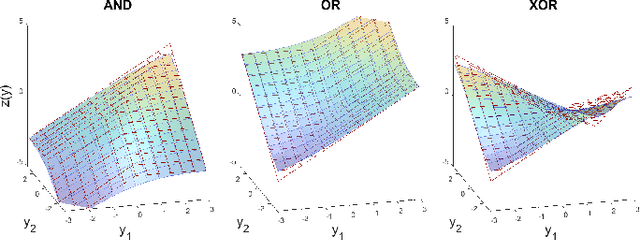
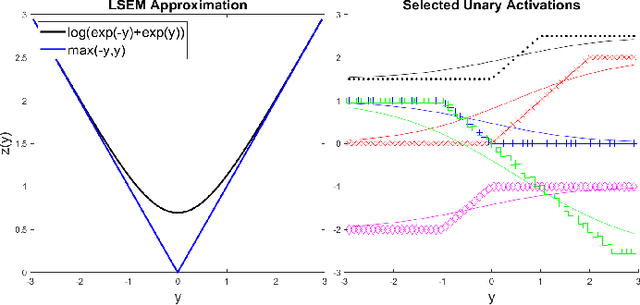
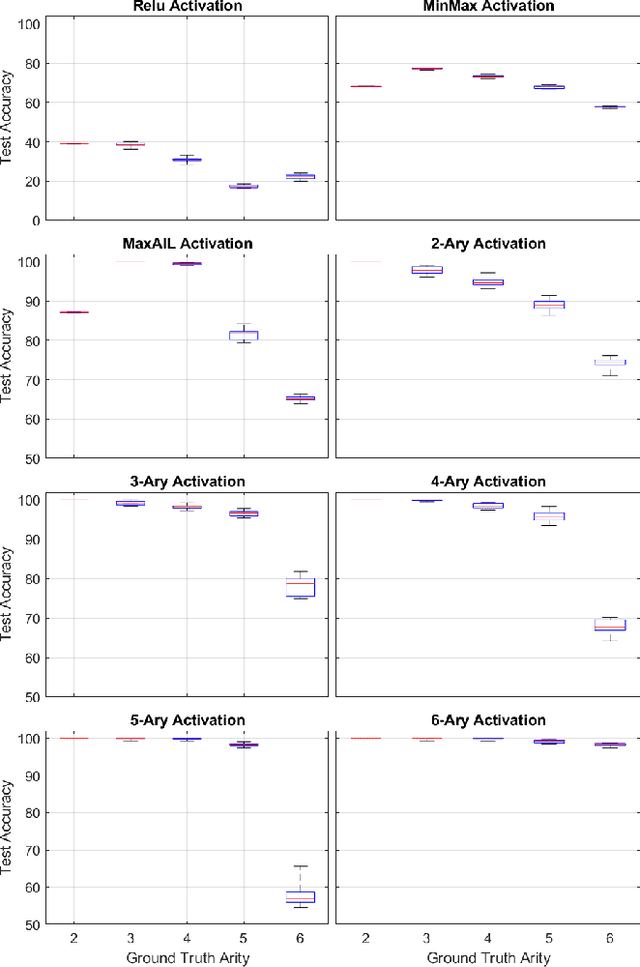
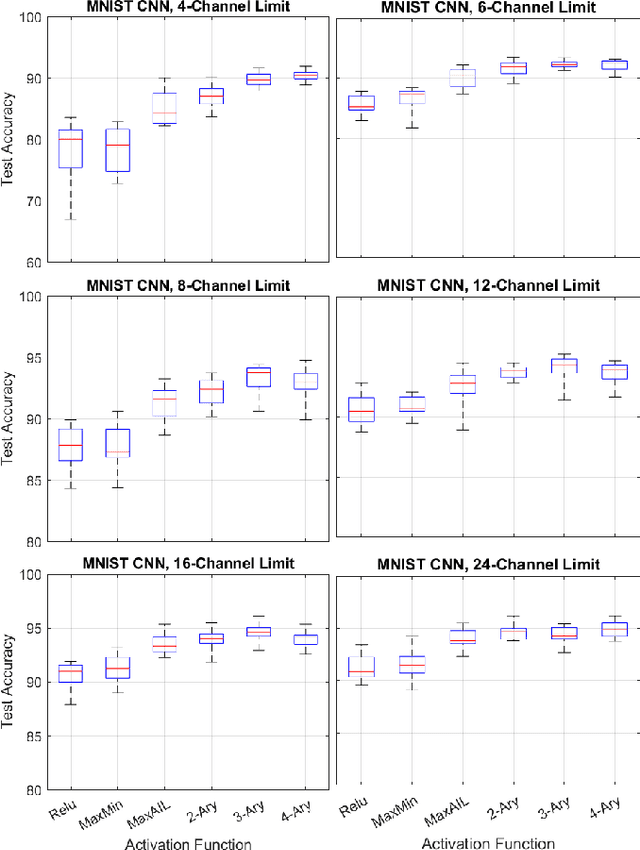
Balancing model complexity against the information contained in observed data is the central challenge to learning. In order for complexity-efficient models to exist and be discoverable in high dimensions, we require a computational framework that relates a credible notion of complexity to simple parameter representations. Further, this framework must allow excess complexity to be gradually removed via gradient-based optimization. Our n-ary, or n-argument, activation functions fill this gap by approximating belief functions (probabilistic Boolean logic) using logit representations of probability. Just as Boolean logic determines the truth of a consequent claim from relationships among a set of antecedent propositions, probabilistic formulations generalize predictions when antecedents, truth tables, and consequents all retain uncertainty. Our activation functions demonstrate the ability to learn arbitrary logic, such as the binary exclusive disjunction (p xor q) and ternary conditioned disjunction ( c ? p : q ), in a single layer using an activation function of matching or greater arity. Further, we represent belief tables using a basis that directly associates the number of nonzero parameters to the effective arity of the belief function, thus capturing a concrete relationship between logical complexity and efficient parameter representations. This opens optimization approaches to reduce logical complexity by inducing parameter sparsity.

Parsimonious Inference

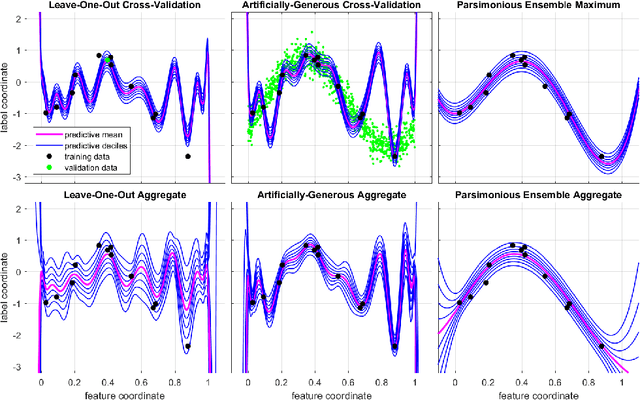
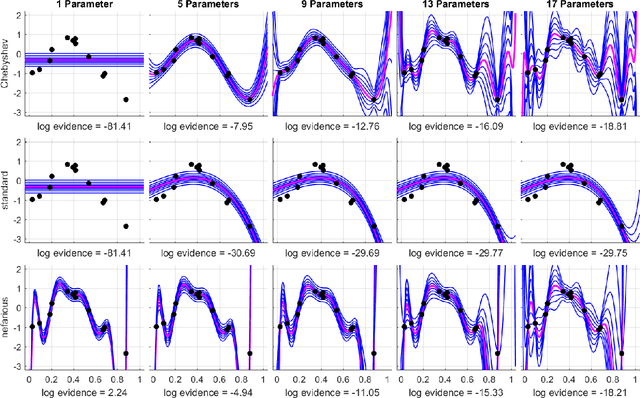
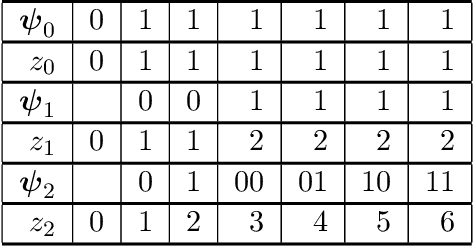
Bayesian inference provides a uniquely rigorous approach to obtain principled justification for uncertainty in predictions, yet it is difficult to articulate suitably general prior belief in the machine learning context, where computational architectures are pure abstractions subject to frequent modifications by practitioners attempting to improve results. Parsimonious inference is an information-theoretic formulation of inference over arbitrary architectures that formalizes Occam's Razor; we prefer simple and sufficient explanations. Our universal hyperprior assigns plausibility to prior descriptions, encoded as sequences of symbols, by expanding on the core relationships between program length, Kolmogorov complexity, and Solomonoff's algorithmic probability. We then cast learning as information minimization over our composite change in belief when an architecture is specified, training data are observed, and model parameters are inferred. By distinguishing model complexity from prediction information, our framework also quantifies the phenomenon of memorization. Although our theory is general, it is most critical when datasets are limited, e.g. small or skewed. We develop novel algorithms for polynomial regression and random forests that are suitable for such data, as demonstrated by our experiments. Our approaches combine efficient encodings with prudent sampling strategies to construct predictive ensembles without cross-validation, thus addressing a fundamental challenge in how to efficiently obtain predictions from data.

Generalizing Information to the Evolution of Rational Belief

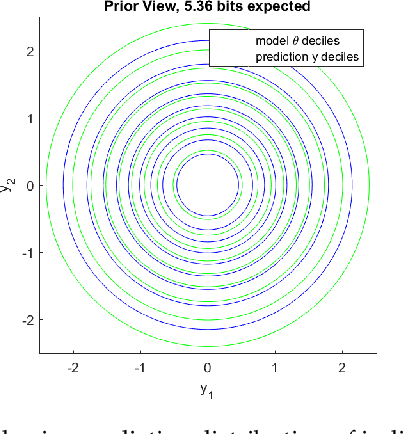
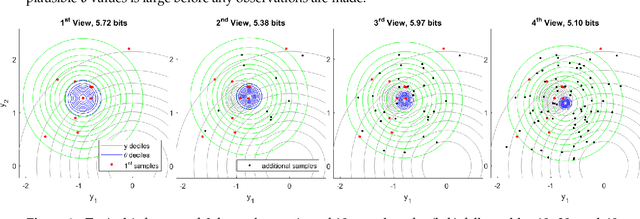
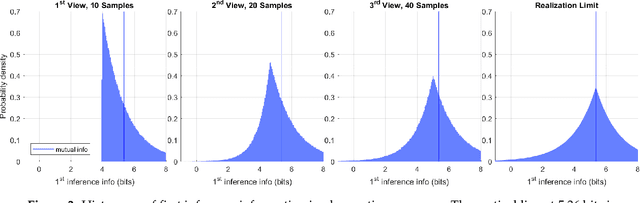
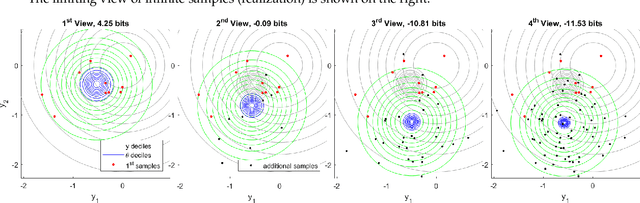
Information theory provides a mathematical foundation to measure uncertainty in belief. Belief is represented by a probability distribution that captures our understanding of an outcome's plausibility. Information measures based on Shannon's concept of entropy include realization information, Kullback-Leibler divergence, Lindley's information in experiment, cross entropy, and mutual information. We derive a general theory of information from first principles that accounts for evolving belief and recovers all of these measures. Rather than simply gauging uncertainty, information is understood in this theory to measure change in belief. We may then regard entropy as the information we expect to gain upon realization of a discrete latent random variable. This theory of information is compatible with the Bayesian paradigm in which rational belief is updated as evidence becomes available. Furthermore, this theory admits novel measures of information with well-defined properties, which we explore in both analysis and experiment. This view of information illuminates the study of machine learning by allowing us to quantify information captured by a predictive model and distinguish it from residual information contained in training data. We gain related insights regarding feature selection, anomaly detection, and novel Bayesian approaches.