Variational Kalman Filtering with Hinf-Based Correction for Robust Bayesian Learning in High Dimensions
Paper and Code
Apr 27, 2022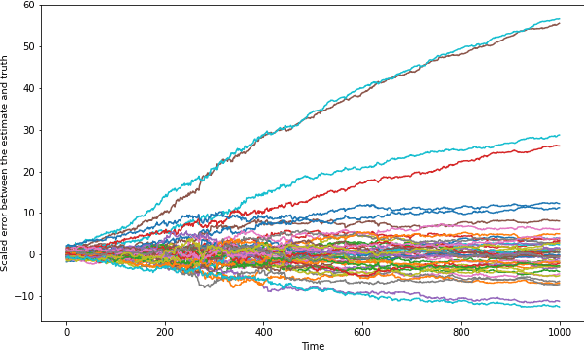
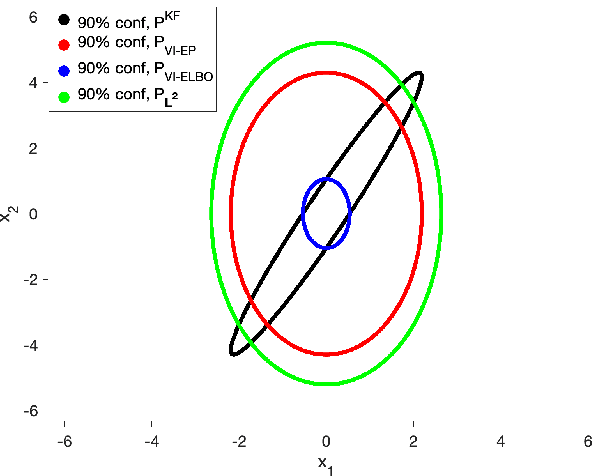
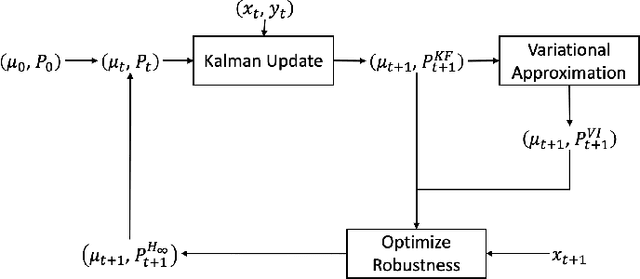
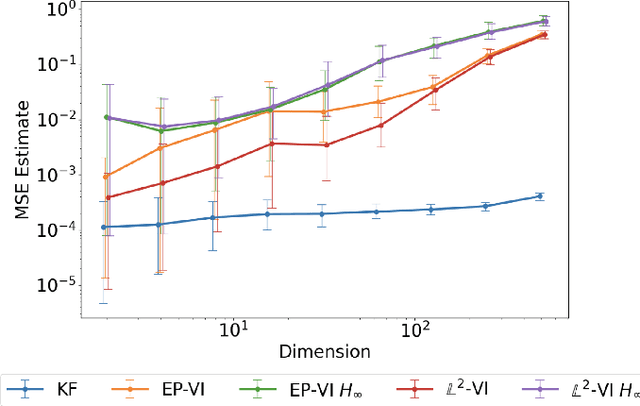
In this paper, we address the problem of convergence of sequential variational inference filter (VIF) through the application of a robust variational objective and Hinf-norm based correction for a linear Gaussian system. As the dimension of state or parameter space grows, performing the full Kalman update with the dense covariance matrix for a large scale system requires increased storage and computational complexity, making it impractical. The VIF approach, based on mean-field Gaussian variational inference, reduces this burden through the variational approximation to the covariance usually in the form of a diagonal covariance approximation. The challenge is to retain convergence and correct for biases introduced by the sequential VIF steps. We desire a framework that improves feasibility while still maintaining reasonable proximity to the optimal Kalman filter as data is assimilated. To accomplish this goal, a Hinf-norm based optimization perturbs the VIF covariance matrix to improve robustness. This yields a novel VIF- Hinf recursion that employs consecutive variational inference and Hinf based optimization steps. We explore the development of this method and investigate a numerical example to illustrate the effectiveness of the proposed filter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge