A Hybrid Deep Neural Operator/Finite Element Method for Ice-Sheet Modeling

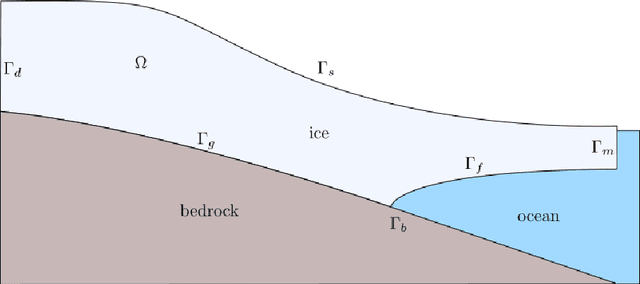
One of the most challenging and consequential problems in climate modeling is to provide probabilistic projections of sea level rise. A large part of the uncertainty of sea level projections is due to uncertainty in ice sheet dynamics. At the moment, accurate quantification of the uncertainty is hindered by the cost of ice sheet computational models. In this work, we develop a hybrid approach to approximate existing ice sheet computational models at a fraction of their cost. Our approach consists of replacing the finite element model for the momentum equations for the ice velocity, the most expensive part of an ice sheet model, with a Deep Operator Network, while retaining a classic finite element discretization for the evolution of the ice thickness. We show that the resulting hybrid model is very accurate and it is an order of magnitude faster than the traditional finite element model. Further, a distinctive feature of the proposed model compared to other neural network approaches, is that it can handle high-dimensional parameter spaces (parameter fields) such as the basal friction at the bed of the glacier, and can therefore be used for generating samples for uncertainty quantification. We study the impact of hyper-parameters, number of unknowns and correlation length of the parameter distribution on the training and accuracy of the Deep Operator Network on a synthetic ice sheet model. We then target the evolution of the Humboldt glacier in Greenland and show that our hybrid model can provide accurate statistics of the glacier mass loss and can be effectively used to accelerate the quantification of uncertainty.

Multifidelity Deep Operator Networks

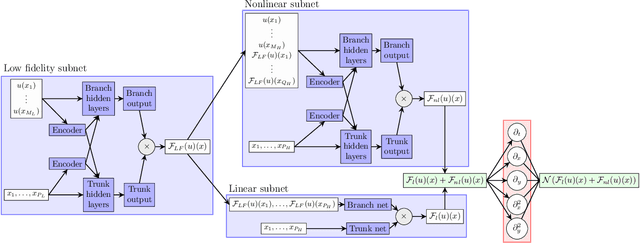
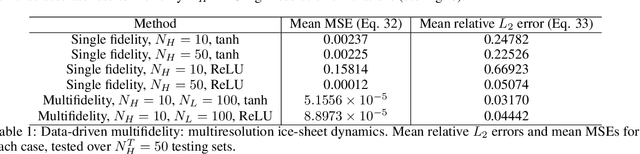
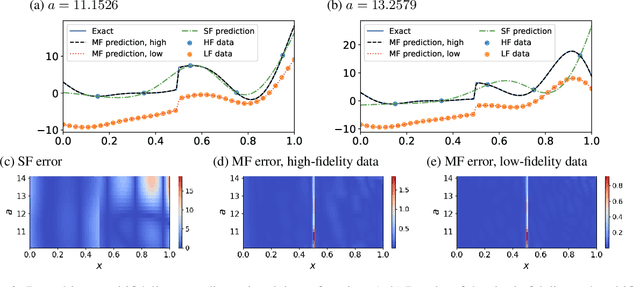
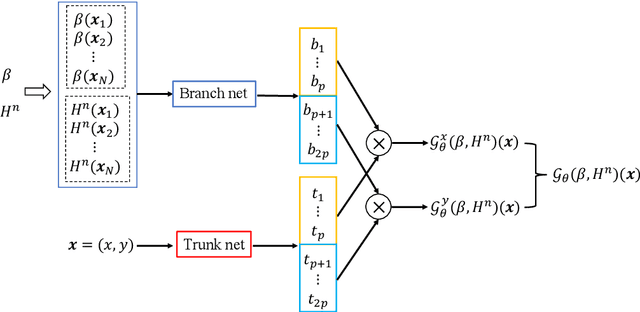
Operator learning for complex nonlinear operators is increasingly common in modeling physical systems. However, training machine learning methods to learn such operators requires a large amount of expensive, high-fidelity data. In this work, we present a composite Deep Operator Network (DeepONet) for learning using two datasets with different levels of fidelity, to accurately learn complex operators when sufficient high-fidelity data is not available. Additionally, we demonstrate that the presence of low-fidelity data can improve the predictions of physics-informed learning with DeepONets.

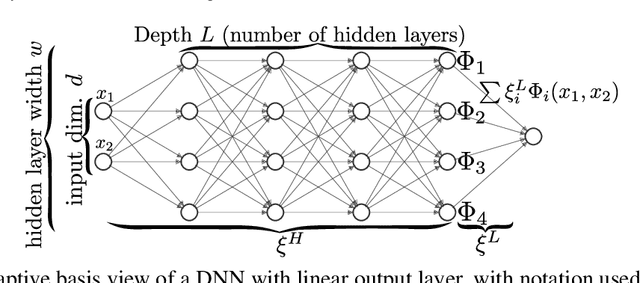
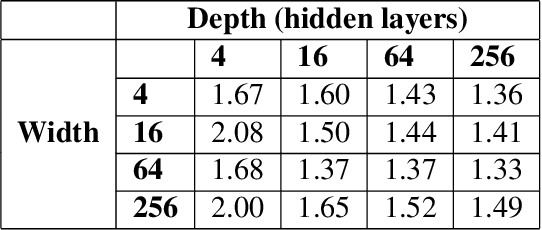
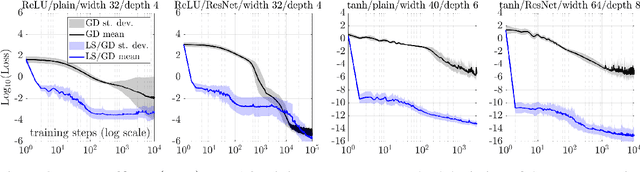
Robust Training and Initialization of Deep Neural Networks: An Adaptive Basis Viewpoint

Motivated by the gap between theoretical optimal approximation rates of deep neural networks (DNNs) and the accuracy realized in practice, we seek to improve the training of DNNs. The adoption of an adaptive basis viewpoint of DNNs leads to novel initializations and a hybrid least squares/gradient descent optimizer. We provide analysis of these techniques and illustrate via numerical examples dramatic increases in accuracy and convergence rate for benchmarks characterizing scientific applications where DNNs are currently used, including regression problems and physics-informed neural networks for the solution of partial differential equations.