Differentiable Neural-Integrated Meshfree Method for Forward and Inverse Modeling of Finite Strain Hyperelasticity

The present study aims to extend the novel physics-informed machine learning approach, specifically the neural-integrated meshfree (NIM) method, to model finite-strain problems characterized by nonlinear elasticity and large deformations. To this end, the hyperelastic material models are integrated into the loss function of the NIM method by employing a consistent local variational formulation. Thanks to the inherent differentiable programming capabilities, NIM can circumvent the need for derivation of Newton-Raphson linearization of the variational form and the resulting tangent stiffness matrix, typically required in traditional numerical methods. Additionally, NIM utilizes a hybrid neural-numerical approximation encoded with partition-of-unity basis functions, coined NeuroPU, to effectively represent the displacement and streamline the training process. NeuroPU can also be used for approximating the unknown material fields, enabling NIM a unified framework for both forward and inverse modeling. For the imposition of displacement boundary conditions, this study introduces a new approach based on singular kernel functions into the NeuroPU approximation, leveraging its unique feature that allows for customized basis functions. Numerical experiments demonstrate the NIM method's capability in forward hyperelasticity modeling, achieving desirable accuracy, with errors among $10^{-3} \sim 10^{-5}$ in the relative $L_2$ norm, comparable to the well-established finite element solvers. Furthermore, NIM is applied to address the complex task of identifying heterogeneous mechanical properties of hyperelastic materials from strain data, validating its effectiveness in the inverse modeling of nonlinear materials. To leverage GPU acceleration, NIM is fully implemented on the JAX deep learning framework in this study, utilizing the accelerator-oriented array computation capabilities offered by JAX.

Neural-Integrated Meshfree (NIM) Method: A differentiable programming-based hybrid solver for computational mechanics

We present the neural-integrated meshfree (NIM) method, a differentiable programming-based hybrid meshfree approach within the field of computational mechanics. NIM seamlessly integrates traditional physics-based meshfree discretization techniques with deep learning architectures. It employs a hybrid approximation scheme, NeuroPU, to effectively represent the solution by combining continuous DNN representations with partition of unity (PU) basis functions associated with the underlying spatial discretization. This neural-numerical hybridization not only enhances the solution representation through functional space decomposition but also reduces both the size of DNN model and the need for spatial gradient computations based on automatic differentiation, leading to a significant improvement in training efficiency. Under the NIM framework, we propose two truly meshfree solvers: the strong form-based NIM (S-NIM) and the local variational form-based NIM (V-NIM). In the S-NIM solver, the strong-form governing equation is directly considered in the loss function, while the V-NIM solver employs a local Petrov-Galerkin approach that allows the construction of variational residuals based on arbitrary overlapping subdomains. This ensures both the satisfaction of underlying physics and the preservation of meshfree property. We perform extensive numerical experiments on both stationary and transient benchmark problems to assess the effectiveness of the proposed NIM methods in terms of accuracy, scalability, generalizability, and convergence properties. Moreover, comparative analysis with other physics-informed machine learning methods demonstrates that NIM, especially V-NIM, significantly enhances both accuracy and efficiency in end-to-end predictive capabilities.

A Hybrid Deep Neural Operator/Finite Element Method for Ice-Sheet Modeling

One of the most challenging and consequential problems in climate modeling is to provide probabilistic projections of sea level rise. A large part of the uncertainty of sea level projections is due to uncertainty in ice sheet dynamics. At the moment, accurate quantification of the uncertainty is hindered by the cost of ice sheet computational models. In this work, we develop a hybrid approach to approximate existing ice sheet computational models at a fraction of their cost. Our approach consists of replacing the finite element model for the momentum equations for the ice velocity, the most expensive part of an ice sheet model, with a Deep Operator Network, while retaining a classic finite element discretization for the evolution of the ice thickness. We show that the resulting hybrid model is very accurate and it is an order of magnitude faster than the traditional finite element model. Further, a distinctive feature of the proposed model compared to other neural network approaches, is that it can handle high-dimensional parameter spaces (parameter fields) such as the basal friction at the bed of the glacier, and can therefore be used for generating samples for uncertainty quantification. We study the impact of hyper-parameters, number of unknowns and correlation length of the parameter distribution on the training and accuracy of the Deep Operator Network on a synthetic ice sheet model. We then target the evolution of the Humboldt glacier in Greenland and show that our hybrid model can provide accurate statistics of the glacier mass loss and can be effectively used to accelerate the quantification of uncertainty.

Physics-Informed Neural Network Method for Parabolic Differential Equations with Sharply Perturbed Initial Conditions

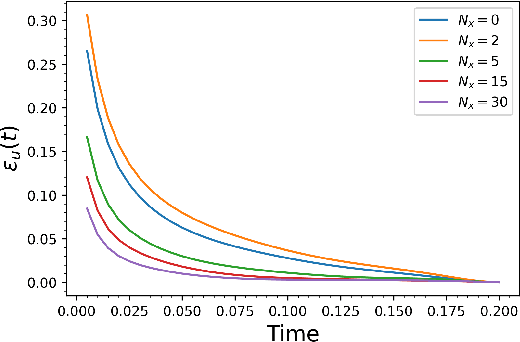
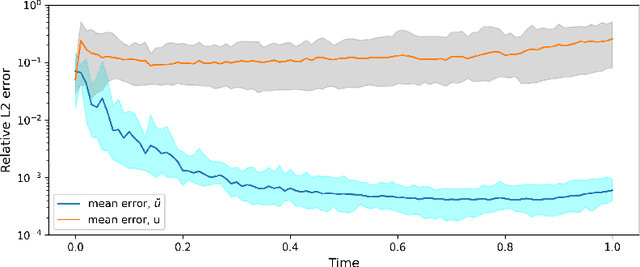
In this paper, we develop a physics-informed neural network (PINN) model for parabolic problems with a sharply perturbed initial condition. As an example of a parabolic problem, we consider the advection-dispersion equation (ADE) with a point (Gaussian) source initial condition. In the $d$-dimensional ADE, perturbations in the initial condition decay with time $t$ as $t^{-d/2}$, which can cause a large approximation error in the PINN solution. Localized large gradients in the ADE solution make the (common in PINN) Latin hypercube sampling of the equation's residual highly inefficient. Finally, the PINN solution of parabolic equations is sensitive to the choice of weights in the loss function. We propose a normalized form of ADE where the initial perturbation of the solution does not decrease in amplitude and demonstrate that this normalization significantly reduces the PINN approximation error. We propose criteria for weights in the loss function that produce a more accurate PINN solution than those obtained with the weights selected via other methods. Finally, we proposed an adaptive sampling scheme that significantly reduces the PINN solution error for the same number of the sampling (residual) points. We demonstrate the accuracy of the proposed PINN model for forward, inverse, and backward ADEs.

Enhanced physics-constrained deep neural networks for modeling vanadium redox flow battery

Numerical modeling and simulation have become indispensable tools for advancing a comprehensive understanding of the underlying mechanisms and cost-effective process optimization and control of flow batteries. In this study, we propose an enhanced version of the physics-constrained deep neural network (PCDNN) approach [1] to provide high-accuracy voltage predictions in the vanadium redox flow batteries (VRFBs). The purpose of the PCDNN approach is to enforce the physics-based zero-dimensional (0D) VRFB model in a neural network to assure model generalization for various battery operation conditions. Limited by the simplifications of the 0D model, the PCDNN cannot capture sharp voltage changes in the extreme SOC regions. To improve the accuracy of voltage prediction at extreme ranges, we introduce a second (enhanced) DNN to mitigate the prediction errors carried from the 0D model itself and call the resulting approach enhanced PCDNN (ePCDNN). By comparing the model prediction with experimental data, we demonstrate that the ePCDNN approach can accurately capture the voltage response throughout the charge--discharge cycle, including the tail region of the voltage discharge curve. Compared to the standard PCDNN, the prediction accuracy of the ePCDNN is significantly improved. The loss function for training the ePCDNN is designed to be flexible by adjusting the weights of the physics-constrained DNN and the enhanced DNN. This allows the ePCDNN framework to be transferable to battery systems with variable physical model fidelity.

Physics-constrained deep neural network method for estimating parameters in a redox flow battery

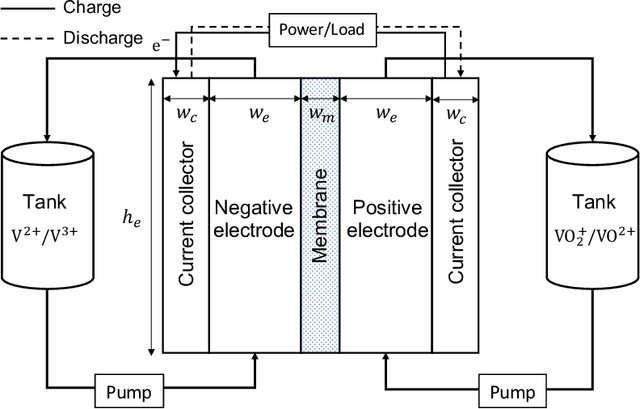
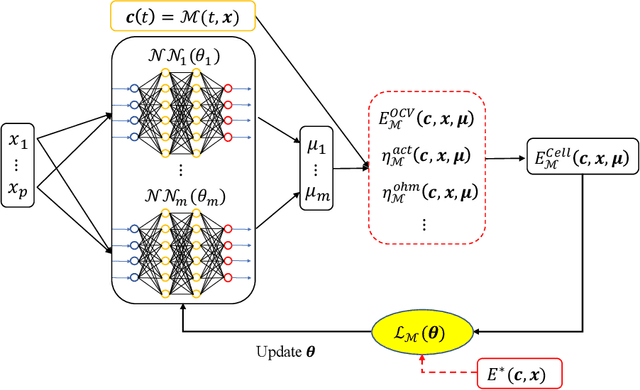
In this paper, we present a physics-constrained deep neural network (PCDNN) method for parameter estimation in the zero-dimensional (0D) model of the vanadium redox flow battery (VRFB). In this approach, we use deep neural networks (DNNs) to approximate the model parameters as functions of the operating conditions. This method allows the integration of the VRFB computational models as the physical constraints in the parameter learning process, leading to enhanced accuracy of parameter estimation and cell voltage prediction. Using an experimental dataset, we demonstrate that the PCDNN method can estimate model parameters for a range of operating conditions and improve the 0D model prediction of voltage compared to the 0D model prediction with constant operation-condition-independent parameters estimated with traditional inverse methods. We also demonstrate that the PCDNN approach has an improved generalization ability for estimating parameter values for operating conditions not used in the DNN training.

Physics-Informed Neural Networks for Multiphysics Data Assimilation with Application to Subsurface Transport

Data assimilation for parameter and state estimation in subsurface transport problems remains a significant challenge due to the sparsity of measurements, the heterogeneity of porous media, and the high computational cost of forward numerical models. We present a physics-informed deep neural networks (DNNs) machine learning method for estimating space-dependent hydraulic conductivity, hydraulic head, and concentration fields from sparse measurements. In this approach, we employ individual DNNs to approximate the unknown parameters (e.g., hydraulic conductivity) and states (e.g., hydraulic head and concentration) of a physical system, and jointly train these DNNs by minimizing the loss function that consists of the governing equations residuals in addition to the error with respect to measurement data. We apply this approach to assimilate conductivity, hydraulic head, and concentration measurements for joint inversion of the conductivity, hydraulic head, and concentration fields in a steady-state advection--dispersion problem. We study the accuracy of the physics-informed DNN approach with respect to data size, number of variables (conductivity and head versus conductivity, head, and concentration), DNNs size, and DNN initialization during training. We demonstrate that the physics-informed DNNs are significantly more accurate than standard data-driven DNNs when the training set consists of sparse data. We also show that the accuracy of parameter estimation increases as additional variables are inverted jointly.