Mathematics of Digital Twins and Transfer Learning for PDE Models

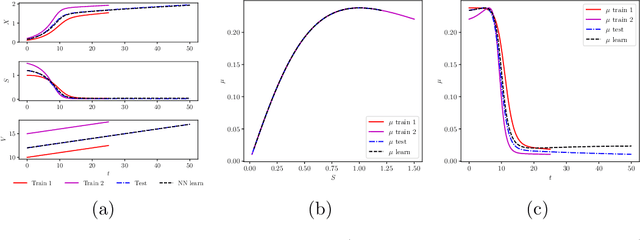
We define a digital twin (DT) of a physical system governed by partial differential equations (PDEs) as a model for real-time simulations and control of the system behavior under changing conditions. We construct DTs using the Karhunen-Lo\`{e}ve Neural Network (KL-NN) surrogate model and transfer learning (TL). The surrogate model allows fast inference and differentiability with respect to control parameters for control and optimization. TL is used to retrain the model for new conditions with minimal additional data. We employ the moment equations to analyze TL and identify parameters that can be transferred to new conditions. The proposed analysis also guides the control variable selection in DT to facilitate efficient TL. For linear PDE problems, the non-transferable parameters in the KL-NN surrogate model can be exactly estimated from a single solution of the PDE corresponding to the mean values of the control variables under new target conditions. Retraining an ML model with a single solution sample is known as one-shot learning, and our analysis shows that the one-shot TL is exact for linear PDEs. For nonlinear PDE problems, transferring of any parameters introduces errors. For a nonlinear diffusion PDE model, we find that for a relatively small range of control variables, some surrogate model parameters can be transferred without introducing a significant error, some can be approximately estimated from the mean-field equation, and the rest can be found using a linear residual least square problem or an ordinary linear least square problem if a small labeled dataset for new conditions is available. The former approach results in a one-shot TL while the latter approach is an example of a few-shot TL. Both methods are approximate for the nonlinear PDEs.

Differentiable modeling to unify machine learning and physical models and advance Geosciences

Process-Based Modeling (PBM) and Machine Learning (ML) are often perceived as distinct paradigms in the geosciences. Here we present differentiable geoscientific modeling as a powerful pathway toward dissolving the perceived barrier between them and ushering in a paradigm shift. For decades, PBM offered benefits in interpretability and physical consistency but struggled to efficiently leverage large datasets. ML methods, especially deep networks, presented strong predictive skills yet lacked the ability to answer specific scientific questions. While various methods have been proposed for ML-physics integration, an important underlying theme -- differentiable modeling -- is not sufficiently recognized. Here we outline the concepts, applicability, and significance of differentiable geoscientific modeling (DG). "Differentiable" refers to accurately and efficiently calculating gradients with respect to model variables, critically enabling the learning of high-dimensional unknown relationships. DG refers to a range of methods connecting varying amounts of prior knowledge to neural networks and training them together, capturing a different scope than physics-guided machine learning and emphasizing first principles. Preliminary evidence suggests DG offers better interpretability and causality than ML, improved generalizability and extrapolation capability, and strong potential for knowledge discovery, while approaching the performance of purely data-driven ML. DG models require less training data while scaling favorably in performance and efficiency with increasing amounts of data. With DG, geoscientists may be better able to frame and investigate questions, test hypotheses, and discover unrecognized linkages.

Enhanced physics-constrained deep neural networks for modeling vanadium redox flow battery

Numerical modeling and simulation have become indispensable tools for advancing a comprehensive understanding of the underlying mechanisms and cost-effective process optimization and control of flow batteries. In this study, we propose an enhanced version of the physics-constrained deep neural network (PCDNN) approach [1] to provide high-accuracy voltage predictions in the vanadium redox flow batteries (VRFBs). The purpose of the PCDNN approach is to enforce the physics-based zero-dimensional (0D) VRFB model in a neural network to assure model generalization for various battery operation conditions. Limited by the simplifications of the 0D model, the PCDNN cannot capture sharp voltage changes in the extreme SOC regions. To improve the accuracy of voltage prediction at extreme ranges, we introduce a second (enhanced) DNN to mitigate the prediction errors carried from the 0D model itself and call the resulting approach enhanced PCDNN (ePCDNN). By comparing the model prediction with experimental data, we demonstrate that the ePCDNN approach can accurately capture the voltage response throughout the charge--discharge cycle, including the tail region of the voltage discharge curve. Compared to the standard PCDNN, the prediction accuracy of the ePCDNN is significantly improved. The loss function for training the ePCDNN is designed to be flexible by adjusting the weights of the physics-constrained DNN and the enhanced DNN. This allows the ePCDNN framework to be transferable to battery systems with variable physical model fidelity.

Machine Learning in Heterogeneous Porous Materials

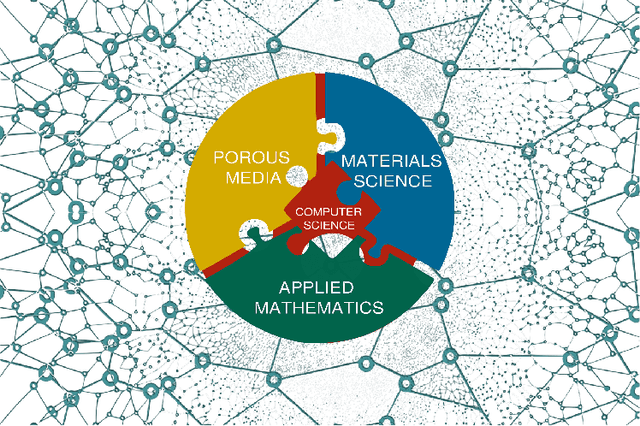
The "Workshop on Machine learning in heterogeneous porous materials" brought together international scientific communities of applied mathematics, porous media, and material sciences with experts in the areas of heterogeneous materials, machine learning (ML) and applied mathematics to identify how ML can advance materials research. Within the scope of ML and materials research, the goal of the workshop was to discuss the state-of-the-art in each community, promote crosstalk and accelerate multi-disciplinary collaborative research, and identify challenges and opportunities. As the end result, four topic areas were identified: ML in predicting materials properties, and discovery and design of novel materials, ML in porous and fractured media and time-dependent phenomena, Multi-scale modeling in heterogeneous porous materials via ML, and Discovery of materials constitutive laws and new governing equations. This workshop was part of the AmeriMech Symposium series sponsored by the National Academies of Sciences, Engineering and Medicine and the U.S. National Committee on Theoretical and Applied Mechanics.

Physics-constrained deep neural network method for estimating parameters in a redox flow battery

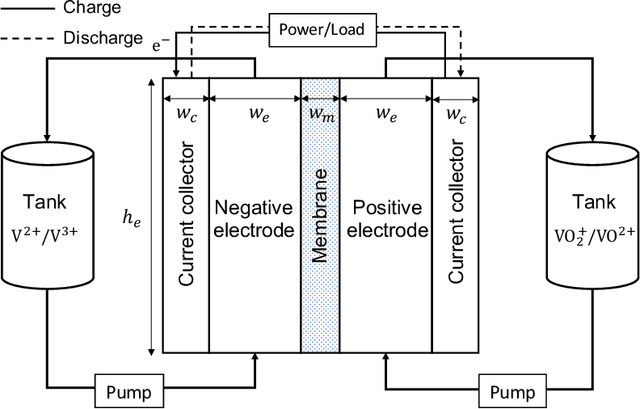
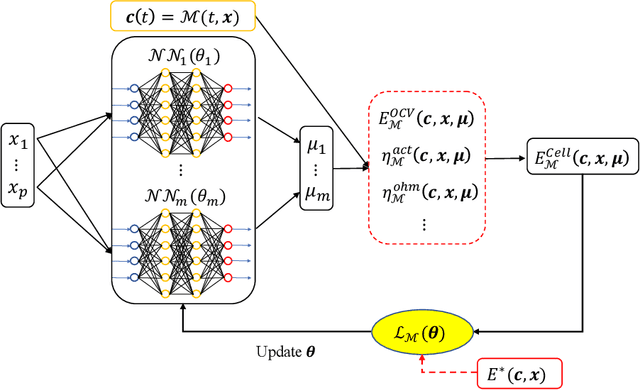
In this paper, we present a physics-constrained deep neural network (PCDNN) method for parameter estimation in the zero-dimensional (0D) model of the vanadium redox flow battery (VRFB). In this approach, we use deep neural networks (DNNs) to approximate the model parameters as functions of the operating conditions. This method allows the integration of the VRFB computational models as the physical constraints in the parameter learning process, leading to enhanced accuracy of parameter estimation and cell voltage prediction. Using an experimental dataset, we demonstrate that the PCDNN method can estimate model parameters for a range of operating conditions and improve the 0D model prediction of voltage compared to the 0D model prediction with constant operation-condition-independent parameters estimated with traditional inverse methods. We also demonstrate that the PCDNN approach has an improved generalization ability for estimating parameter values for operating conditions not used in the DNN training.

Highly-scalable, physics-informed GANs for learning solutions of stochastic PDEs

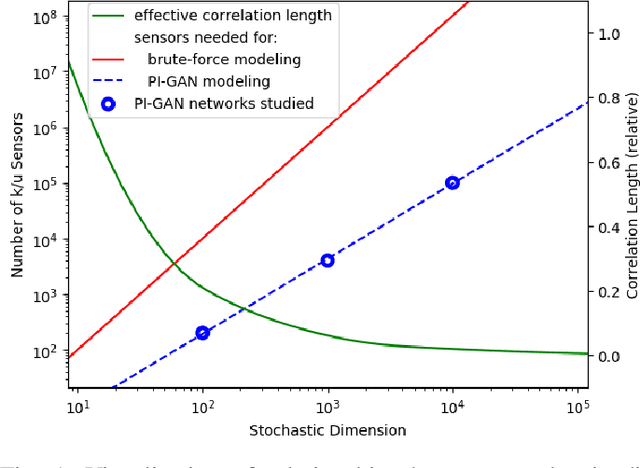
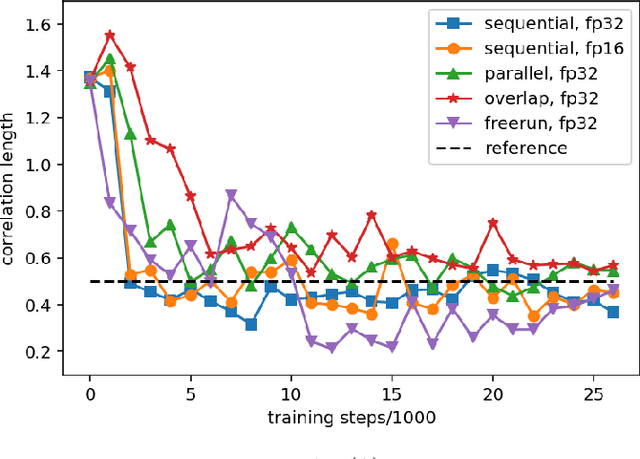
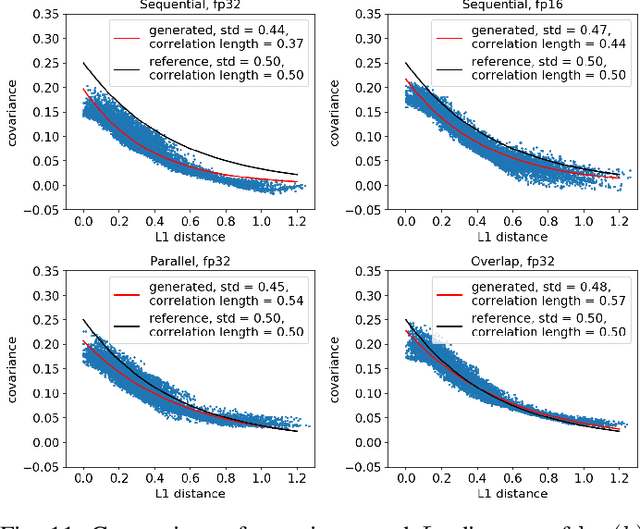
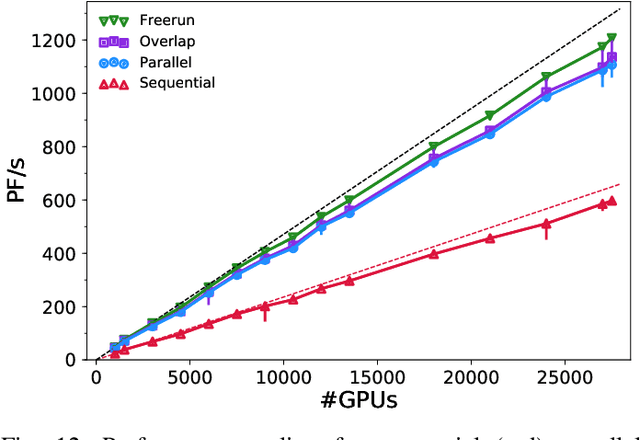
Uncertainty quantification for forward and inverse problems is a central challenge across physical and biomedical disciplines. We address this challenge for the problem of modeling subsurface flow at the Hanford Site by combining stochastic computational models with observational data using physics-informed GAN models. The geographic extent, spatial heterogeneity, and multiple correlation length scales of the Hanford Site require training a computationally intensive GAN model to thousands of dimensions. We develop a hierarchical scheme for exploiting domain parallelism, map discriminators and generators to multiple GPUs, and employ efficient communication schemes to ensure training stability and convergence. We developed a highly optimized implementation of this scheme that scales to 27,500 NVIDIA Volta GPUs and 4584 nodes on the Summit supercomputer with a 93.1% scaling efficiency, achieving peak and sustained half-precision rates of 1228 PF/s and 1207 PF/s.

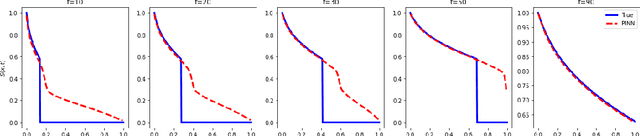
A comparative study of physics-informed neural network models for learning unknown dynamics and constitutive relations

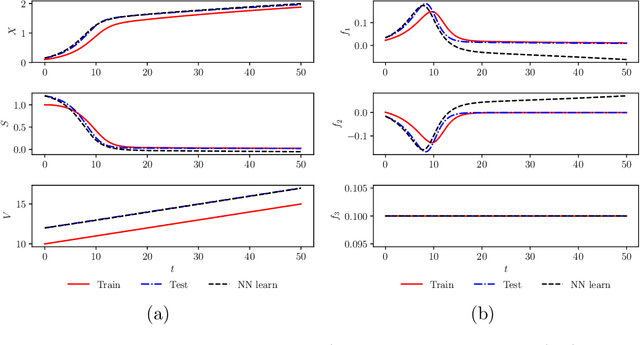
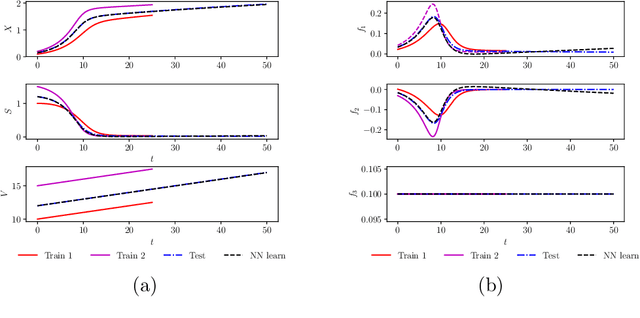
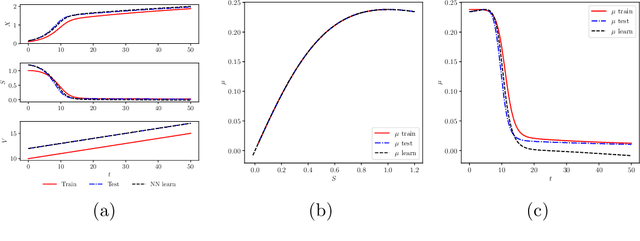
We investigate the use of discrete and continuous versions of physics-informed neural network methods for learning unknown dynamics or constitutive relations of a dynamical system. For the case of unknown dynamics, we represent all the dynamics with a deep neural network (DNN). When the dynamics of the system are known up to the specification of constitutive relations (that can depend on the state of the system), we represent these constitutive relations with a DNN. The discrete versions combine classical multistep discretization methods for dynamical systems with neural network based machine learning methods. On the other hand, the continuous versions utilize deep neural networks to minimize the residual function for the continuous governing equations. We use the case of a fedbatch bioreactor system to study the effectiveness of these approaches and discuss conditions for their applicability. Our results indicate that the accuracy of the trained neural network models is much higher for the cases where we only have to learn a constitutive relation instead of the whole dynamics. This finding corroborates the well-known fact from scientific computing that building as much structural information is available into an algorithm can enhance its efficiency and/or accuracy.

Physics-Informed CoKriging: A Gaussian-Process-Regression-Based Multifidelity Method for Data-Model Convergence

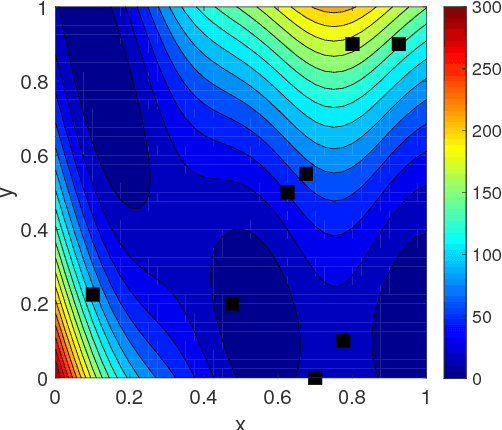
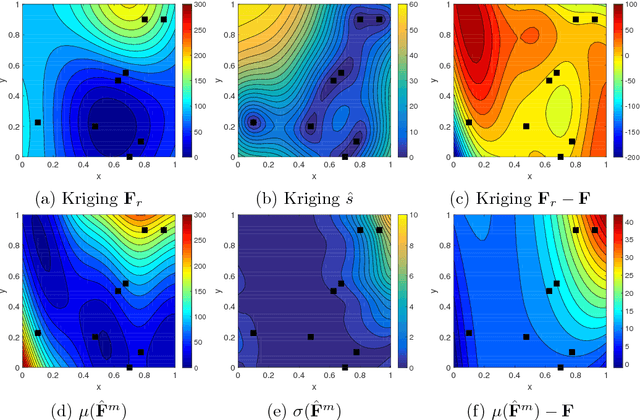
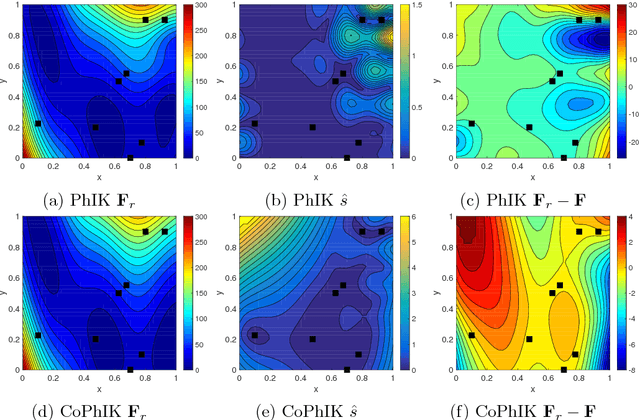
In this work, we propose a new Gaussian process regression (GPR)-based multifidelity method: physics-informed CoKriging (CoPhIK). In CoKriging-based multifidelity methods, the quantities of interest are modeled as linear combinations of multiple parameterized stationary Gaussian processes (GPs), and the hyperparameters of these GPs are estimated from data via optimization. In CoPhIK, we construct a GP representing low-fidelity data using physics-informed Kriging (PhIK), and model the discrepancy between low- and high-fidelity data using a parameterized GP with hyperparameters identified via optimization. Our approach reduces the cost of optimization for inferring hyperparameters by incorporating partial physical knowledge. We prove that the physical constraints in the form of deterministic linear operators are satisfied up to an error bound. Furthermore, we combine CoPhIK with a greedy active learning algorithm for guiding the selection of additional observation locations. The efficiency and accuracy of CoPhIK are demonstrated for reconstructing the partially observed modified Branin function, reconstructing the sparsely observed state of a steady state heat transport problem, and learning a conservative tracer distribution from sparse tracer concentration measurements.

Physics-Informed Kriging: A Physics-Informed Gaussian Process Regression Method for Data-Model Convergence

In this work, we propose a new Gaussian process regression (GPR) method: physics-informed Kriging (PhIK). In the standard data-driven Kriging, the unknown function of interest is usually treated as a Gaussian process with assumed stationary covariance with hyperparameters estimated from data. In PhIK, we compute the mean and covariance function from realizations of available stochastic models, e.g., from realizations of governing stochastic partial differential equations solutions. Such a constructed Gaussian process generally is non-stationary, and does not assume a specific form of the covariance function. Our approach avoids the costly optimization step in data-driven GPR methods to identify the hyperparameters. More importantly, we prove that the physical constraints in the form of a deterministic linear operator are guaranteed in the resulting prediction. We also provide an error estimate in preserving the physical constraints when errors are included in the stochastic model realizations. To reduce the computational cost of obtaining stochastic model realizations, we propose a multilevel Monte Carlo estimate of the mean and covariance functions. Further, we present an active learning algorithm that guides the selection of additional observation locations. The efficiency and accuracy of PhIK are demonstrated for reconstructing a partially known modified Branin function and learning a conservative tracer distribution from sparse concentration measurements.