Deep Generative Data Assimilation in Multimodal Setting

Robust integration of physical knowledge and data is key to improve computational simulations, such as Earth system models. Data assimilation is crucial for achieving this goal because it provides a systematic framework to calibrate model outputs with observations, which can include remote sensing imagery and ground station measurements, with uncertainty quantification. Conventional methods, including Kalman filters and variational approaches, inherently rely on simplifying linear and Gaussian assumptions, and can be computationally expensive. Nevertheless, with the rapid adoption of data-driven methods in many areas of computational sciences, we see the potential of emulating traditional data assimilation with deep learning, especially generative models. In particular, the diffusion-based probabilistic framework has large overlaps with data assimilation principles: both allows for conditional generation of samples with a Bayesian inverse framework. These models have shown remarkable success in text-conditioned image generation or image-controlled video synthesis. Likewise, one can frame data assimilation as observation-conditioned state calibration. In this work, we propose SLAMS: Score-based Latent Assimilation in Multimodal Setting. Specifically, we assimilate in-situ weather station data and ex-situ satellite imagery to calibrate the vertical temperature profiles, globally. Through extensive ablation, we demonstrate that SLAMS is robust even in low-resolution, noisy, and sparse data settings. To our knowledge, our work is the first to apply deep generative framework for multimodal data assimilation using real-world datasets; an important step for building robust computational simulators, including the next-generation Earth system models. Our code is available at: https://github.com/yongquan-qu/SLAMS

Joint Parameter and Parameterization Inference with Uncertainty Quantification through Differentiable Programming

Accurate representations of unknown and sub-grid physical processes through parameterizations (or closure) in numerical simulations with quantified uncertainty are critical for resolving the coarse-grained partial differential equations that govern many problems ranging from weather and climate prediction to turbulence simulations. Recent advances have seen machine learning (ML) increasingly applied to model these subgrid processes, resulting in the development of hybrid physics-ML models through the integration with numerical solvers. In this work, we introduce a novel framework for the joint estimation and uncertainty quantification of physical parameters and machine learning parameterizations in tandem, leveraging differentiable programming. Achieved through online training and efficient Bayesian inference within a high-dimensional parameter space, this approach is enabled by the capabilities of differentiable programming. This proof of concept underscores the substantial potential of differentiable programming in synergistically combining machine learning with differential equations, thereby enhancing the capabilities of hybrid physics-ML modeling.

ChaosBench: A Multi-Channel, Physics-Based Benchmark for Subseasonal-to-Seasonal Climate Prediction

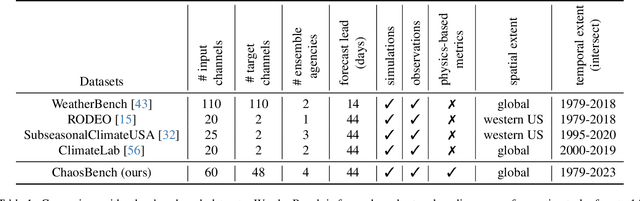
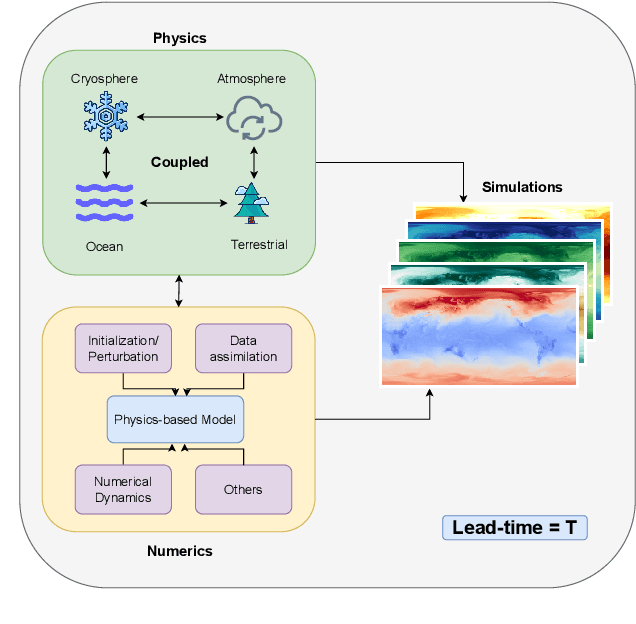
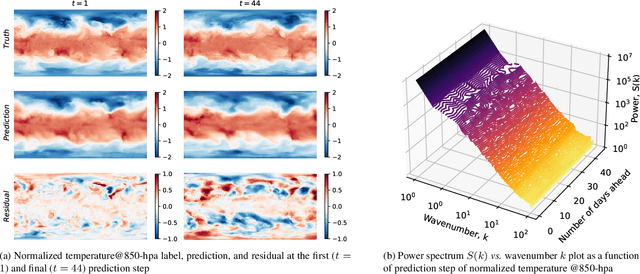
Accurate prediction of climate in the subseasonal-to-seasonal scale is crucial for disaster readiness, reduced economic risk, and improved policy-making amidst climate change. Yet, S2S prediction remains challenging due to the chaotic nature of the system. At present, existing benchmarks for weather and climate applications, tend to (1) have shorter forecasting range of up-to 14 days, (2) do not include a wide range of operational baseline forecasts, and (3) lack physics-based constraints for explainability. Thus, we propose ChaosBench, a large-scale, multi-channel, physics-based benchmark for S2S prediction. ChaosBench has over 460K frames of real-world observations and simulations, each with 60 variable-channels and spanning for up-to 45 years. We also propose several physics-based, in addition to vision-based metrics, that enables for a more physically-consistent model. Furthermore, we include a diverse set of physics-based forecasts from 4 national weather agencies as baselines to our data-driven counterpart. We establish two tasks that vary in complexity: full and sparse dynamics prediction. Our benchmark is one of the first to perform large-scale evaluation on existing models including PanguWeather, FourCastNetV2, GraphCast, and ClimaX, and finds methods originally developed for weather-scale applications fails on S2S task. We release our benchmark code and datasets at https://leap-stc.github.io/ChaosBench.

Simulating the Air Quality Impact of Prescribed Fires Using a Graph Neural Network-Based PM$_{2.5}$ Emissions Forecasting System

The increasing size and severity of wildfires across western North America have generated dangerous levels of PM$_{2.5}$ pollution in recent years. In a warming climate, expanding the use of prescribed fires is widely considered to be the most robust fire mitigation strategy. However, reliably forecasting the potential air quality impact from these prescribed fires, a critical ingredient in determining the fires' location and time, at hourly to daily time scales remains a challenging problem. This paper proposes a novel integration of prescribed fire simulation with a spatio-temporal graph neural network-based PM$_{2.5}$ forecasting model. The experiments in this work focus on determining the optimal time for implementing prescribed fires in California as well as quantifying the potential air quality trade-offs involved in conducting more prescribed fires outside the fire season.

Systematic Sampling and Validation of Machine Learning-Parameterizations in Climate Models

Progress in hybrid physics-machine learning (ML) climate simulations has been limited by the difficulty of obtaining performant coupled (i.e. online) simulations. While evaluating hundreds of ML parameterizations of subgrid closures (here of convection and radiation) offline is straightforward, online evaluation at the same scale is technically challenging. Our software automation achieves an order-of-magnitude larger sampling of online modeling errors than has previously been examined. Using this, we evaluate the hybrid climate model performance and define strategies to improve it. We show that model online performance improves when incorporating memory, a relative humidity input feature transformation, and additional input variables. We also reveal substantial variation in online error and inconsistencies between offline vs. online error statistics. The implication is that hundreds of candidate ML models should be evaluated online to detect the effects of parameterization design choices. This is considerably more sampling than tends to be reported in the current literature.

Transferring climate change knowledge

Accurate climate projections are required for climate adaptation and mitigation. Earth system model simulations, used to project climate change, inherently make approximations in their representation of small-scale physical processes, such as clouds, that are at the root of the uncertainties in global mean temperature's response to increased greenhouse gas concentrations. Several approaches have been developed to use historical observations to constrain future projections and reduce uncertainties in climate projections and climate feedbacks. Yet those methods cannot capture the non-linear complexity inherent in the climate system. Using a Transfer Learning approach, we show that Machine Learning, in particular Deep Neural Networks, can be used to optimally leverage and merge the knowledge gained from Earth system model simulations and historical observations to more accurately project global surface temperature fields in the 21st century. For the Shared Socioeconomic Pathways (SSPs) 2-4.5, 3-7.0 and 5-8.5, we refine regional estimates and the global projection of the average global temperature in 2081-2098 (with respect to the period 1850-1900) to 2.73{\deg}C (2.44-3.11{\deg}C), 3.92{\deg}C (3.5-4.47{\deg}C) and 4.53{\deg}C (3.69-5.5{\deg}C), respectively, compared to the unconstrained 2.7{\deg}C (1.65-3.8{\deg}C), 3.71{\deg}C (2.56-4.97{\deg}C) and 4.47{\deg}C (2.95-6.02{\deg}C). Our findings show that the 1.5{\deg}C threshold of the Paris' agreement will be crossed in 2031 (2028-2034) for SSP2-4.5, in 2029 (2027-2031) for SSP3-7.0 and in 2028 (2025-2031) for SSP5-8.5. Similarly, the 2{\deg}C threshold will be exceeded in 2051 (2045-2059), 2044 (2040-2047) and 2042 (2038-2047) respectively. Our new method provides more accurate climate projections urgently required for climate adaptation.

Multi-fidelity climate model parameterization for better generalization and extrapolation

Machine-learning-based parameterizations (i.e. representation of sub-grid processes) of global climate models or turbulent simulations have recently been proposed as a powerful alternative to physical, but empirical, representations, offering a lower computational cost and higher accuracy. Yet, those approaches still suffer from a lack of generalization and extrapolation beyond the training data, which is however critical to projecting climate change or unobserved regimes of turbulence. Here we show that a multi-fidelity approach, which integrates datasets of different accuracy and abundance, can provide the best of both worlds: the capacity to extrapolate leveraging the physically-based parameterization and a higher accuracy using the machine-learning-based parameterizations. In an application to climate modeling, the multi-fidelity framework yields more accurate climate projections without requiring major increase in computational resources. Our multi-fidelity randomized prior networks (MF-RPNs) combine physical parameterization data as low-fidelity and storm-resolving historical run's data as high-fidelity. To extrapolate beyond the training data, the MF-RPNs are tested on high-fidelity warming scenarios, $+4K$, data. We show the MF-RPN's capacity to return much more skillful predictions compared to either low- or high-fidelity (historical data) simulations trained only on one regime while providing trustworthy uncertainty quantification across a wide range of scenarios. Our approach paves the way for the use of machine-learning based methods that can optimally leverage historical observations or high-fidelity simulations and extrapolate to unseen regimes such as climate change.

ClimSim: An open large-scale dataset for training high-resolution physics emulators in hybrid multi-scale climate simulators

Modern climate projections lack adequate spatial and temporal resolution due to computational constraints. A consequence is inaccurate and imprecise prediction of critical processes such as storms. Hybrid methods that combine physics with machine learning (ML) have introduced a new generation of higher fidelity climate simulators that can sidestep Moore's Law by outsourcing compute-hungry, short, high-resolution simulations to ML emulators. However, this hybrid ML-physics simulation approach requires domain-specific treatment and has been inaccessible to ML experts because of lack of training data and relevant, easy-to-use workflows. We present ClimSim, the largest-ever dataset designed for hybrid ML-physics research. It comprises multi-scale climate simulations, developed by a consortium of climate scientists and ML researchers. It consists of 5.7 billion pairs of multivariate input and output vectors that isolate the influence of locally-nested, high-resolution, high-fidelity physics on a host climate simulator's macro-scale physical state. The dataset is global in coverage, spans multiple years at high sampling frequency, and is designed such that resulting emulators are compatible with downstream coupling into operational climate simulators. We implement a range of deterministic and stochastic regression baselines to highlight the ML challenges and their scoring. The data (https://huggingface.co/datasets/LEAP/ClimSim_high-res) and code (https://leap-stc.github.io/ClimSim) are released openly to support the development of hybrid ML-physics and high-fidelity climate simulations for the benefit of science and society.

Differentiable modeling to unify machine learning and physical models and advance Geosciences

Process-Based Modeling (PBM) and Machine Learning (ML) are often perceived as distinct paradigms in the geosciences. Here we present differentiable geoscientific modeling as a powerful pathway toward dissolving the perceived barrier between them and ushering in a paradigm shift. For decades, PBM offered benefits in interpretability and physical consistency but struggled to efficiently leverage large datasets. ML methods, especially deep networks, presented strong predictive skills yet lacked the ability to answer specific scientific questions. While various methods have been proposed for ML-physics integration, an important underlying theme -- differentiable modeling -- is not sufficiently recognized. Here we outline the concepts, applicability, and significance of differentiable geoscientific modeling (DG). "Differentiable" refers to accurately and efficiently calculating gradients with respect to model variables, critically enabling the learning of high-dimensional unknown relationships. DG refers to a range of methods connecting varying amounts of prior knowledge to neural networks and training them together, capturing a different scope than physics-guided machine learning and emphasizing first principles. Preliminary evidence suggests DG offers better interpretability and causality than ML, improved generalizability and extrapolation capability, and strong potential for knowledge discovery, while approaching the performance of purely data-driven ML. DG models require less training data while scaling favorably in performance and efficiency with increasing amounts of data. With DG, geoscientists may be better able to frame and investigate questions, test hypotheses, and discover unrecognized linkages.

History-Based, Bayesian, Closure for Stochastic Parameterization: Application to Lorenz '96

Physical parameterizations are used as representations of unresolved subgrid processes within weather and global climate models or coarse-scale turbulent models, whose resolutions are too coarse to resolve small-scale processes. These parameterizations are typically grounded on physically-based, yet empirical, representations of the underlying small-scale processes. Machine learning-based parameterizations have recently been proposed as an alternative and have shown great promises to reduce uncertainties associated with small-scale processes. Yet, those approaches still show some important mismatches that are often attributed to stochasticity in the considered process. This stochasticity can be due to noisy data, unresolved variables or simply to the inherent chaotic nature of the process. To address these issues, we develop a new type of parameterization (closure) which is based on a Bayesian formalism for neural networks, to account for uncertainty quantification, and includes memory, to account for the non-instantaneous response of the closure. To overcome the curse of dimensionality of Bayesian techniques in high-dimensional spaces, the Bayesian strategy is based on a Hamiltonian Monte Carlo Markov Chain sampling strategy that takes advantage of the likelihood function and kinetic energy's gradients with respect to the parameters to accelerate the sampling process. We apply the proposed Bayesian history-based parameterization to the Lorenz '96 model in the presence of noisy and sparse data, similar to satellite observations, and show its capacity to predict skillful forecasts of the resolved variables while returning trustworthy uncertainty quantifications for different sources of error. This approach paves the way for the use of Bayesian approaches for closure problems.