Producing Plankton Classifiers that are Robust to Dataset Shift

Modern plankton high-throughput monitoring relies on deep learning classifiers for species recognition in water ecosystems. Despite satisfactory nominal performances, a significant challenge arises from Dataset Shift, which causes performances to drop during deployment. In our study, we integrate the ZooLake dataset with manually-annotated images from 10 independent days of deployment, serving as test cells to benchmark Out-Of-Dataset (OOD) performances. Our analysis reveals instances where classifiers, initially performing well in In-Dataset conditions, encounter notable failures in practical scenarios. For example, a MobileNet with a 92% nominal test accuracy shows a 77% OOD accuracy. We systematically investigate conditions leading to OOD performance drops and propose a preemptive assessment method to identify potential pitfalls when classifying new data, and pinpoint features in OOD images that adversely impact classification. We present a three-step pipeline: (i) identifying OOD degradation compared to nominal test performance, (ii) conducting a diagnostic analysis of degradation causes, and (iii) providing solutions. We find that ensembles of BEiT vision transformers, with targeted augmentations addressing OOD robustness, geometric ensembling, and rotation-based test-time augmentation, constitute the most robust model, which we call BEsT model. It achieves an 83% OOD accuracy, with errors concentrated on container classes. Moreover, it exhibits lower sensitivity to dataset shift, and reproduces well the plankton abundances. Our proposed pipeline is applicable to generic plankton classifiers, contingent on the availability of suitable test cells. By identifying critical shortcomings and offering practical procedures to fortify models against dataset shift, our study contributes to the development of more reliable plankton classification technologies.

Initial Guessing Bias: How Untrained Networks Favor Some Classes

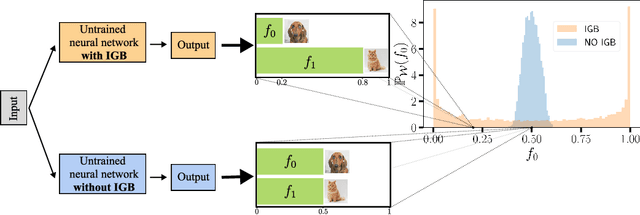
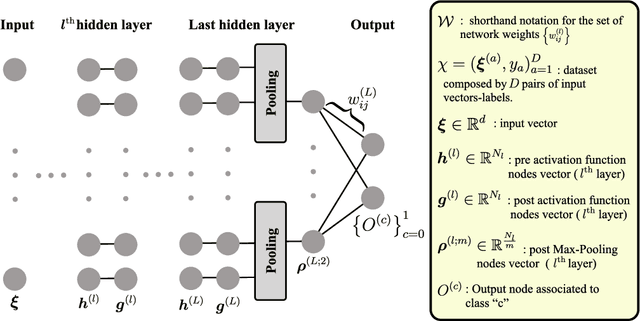
The initial state of neural networks plays a central role in conditioning the subsequent training dynamics. In the context of classification problems, we provide a theoretical analysis demonstrating that the structure of a neural network can condition the model to assign all predictions to the same class, even before the beginning of training, and in the absence of explicit biases. We show that the presence of this phenomenon, which we call "Initial Guessing Bias" (IGB), depends on architectural choices such as activation functions, max-pooling layers, and network depth. Our analysis of IGB has practical consequences, in that it guides architecture selection and initialization. We also highlight theoretical consequences, such as the breakdown of node-permutation symmetry, the violation of self-averaging, the validity of some mean-field approximations, and the non-trivial differences arising with depth.

Differentiable modeling to unify machine learning and physical models and advance Geosciences

Process-Based Modeling (PBM) and Machine Learning (ML) are often perceived as distinct paradigms in the geosciences. Here we present differentiable geoscientific modeling as a powerful pathway toward dissolving the perceived barrier between them and ushering in a paradigm shift. For decades, PBM offered benefits in interpretability and physical consistency but struggled to efficiently leverage large datasets. ML methods, especially deep networks, presented strong predictive skills yet lacked the ability to answer specific scientific questions. While various methods have been proposed for ML-physics integration, an important underlying theme -- differentiable modeling -- is not sufficiently recognized. Here we outline the concepts, applicability, and significance of differentiable geoscientific modeling (DG). "Differentiable" refers to accurately and efficiently calculating gradients with respect to model variables, critically enabling the learning of high-dimensional unknown relationships. DG refers to a range of methods connecting varying amounts of prior knowledge to neural networks and training them together, capturing a different scope than physics-guided machine learning and emphasizing first principles. Preliminary evidence suggests DG offers better interpretability and causality than ML, improved generalizability and extrapolation capability, and strong potential for knowledge discovery, while approaching the performance of purely data-driven ML. DG models require less training data while scaling favorably in performance and efficiency with increasing amounts of data. With DG, geoscientists may be better able to frame and investigate questions, test hypotheses, and discover unrecognized linkages.

Characterizing the Effect of Class Imbalance on the Learning Dynamics

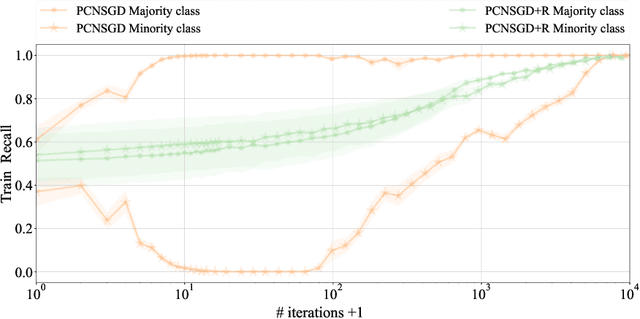
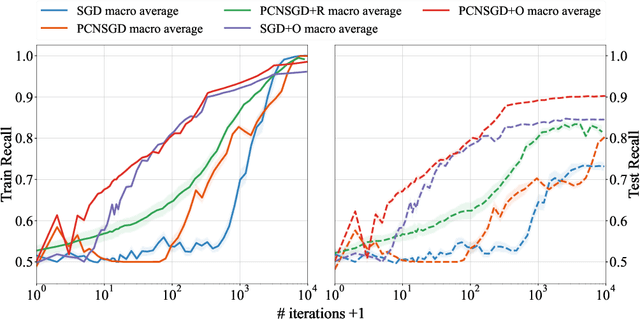
Data imbalance is a common problem in the machine learning literature that can have a critical effect on the performance of a model. Various solutions exist - such as the ones that focus on resampling or data generation - but their impact on the convergence of gradient-based optimizers used in deep learning is not understood. We here elucidate the significant negative impact of data imbalance on learning, showing that the learning curves for minority and majority classes follow sub-optimal trajectories when training with a gradient-based optimizer. The reason is not only that the gradient signal neglects the minority classes, but also that the minority classes are subject to a larger directional noise, which slows their learning by an amount related to the imbalance ratio. To address this problem, we propose a new algorithmic solution, for which we provide a detailed analysis of its convergence behavior. We show both theoretically and empirically that this new algorithm exhibits a better behavior with more stable learning curves for each class, as well as a better generalization performance.

Predicting Chemical Hazard across Taxa through Machine Learning

We apply machine learning methods to predict chemical hazards focusing on fish acute toxicity across taxa. We analyze the relevance of taxonomy and experimental setup, and show that taking them into account can lead to considerable improvements in the classification performance. We quantify the gain obtained by introducing the taxonomic and experimental information, compared to classifying based on chemical information alone. We use our approach with standard machine learning models (K-nearest neighbors, random forests and deep neural networks), as well as the recently proposed Read-Across Structure Activity Relationship (RASAR) models, which were very successful in predicting chemical hazards to mammals based on chemical similarity. We are able to obtain accuracies of over 0.93 on datasets where, due to noise in the data, the maximum achievable accuracy is expected to be below 0.95, which results in an effective accuracy of 0.98. The best performances are obtained by random forests and RASAR models. We analyze metrics to compare our results with animal test reproducibility, and despite most of our models 'outperform animal test reproducibility' as measured through recently proposed metrics, we show that the comparison between machine learning performance and animal test reproducibility should be addressed with particular care. While we focus on fish mortality, our approach, provided that the right data is available, is valid for any combination of chemicals, effects and taxa.

The jamming transition as a paradigm to understand the loss landscape of deep neural networks

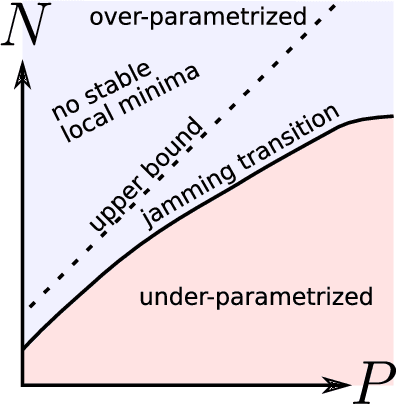
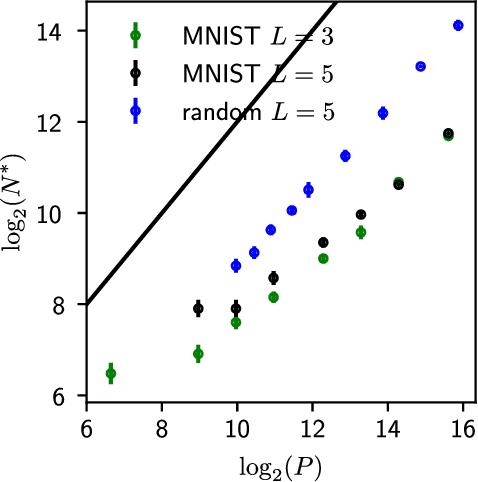
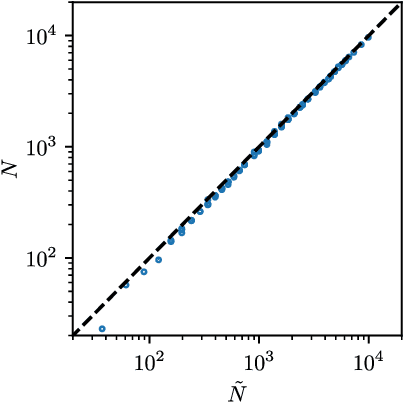
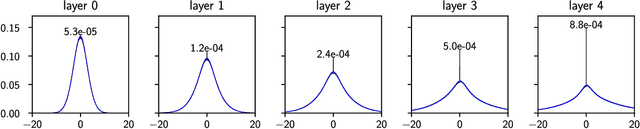
Deep learning has been immensely successful at a variety of tasks, ranging from classification to AI. Learning corresponds to fitting training data, which is implemented by descending a very high-dimensional loss function. Understanding under which conditions neural networks do not get stuck in poor minima of the loss, and how the landscape of that loss evolves as depth is increased remains a challenge. Here we predict, and test empirically, an analogy between this landscape and the energy landscape of repulsive ellipses. We argue that in FC networks a phase transition delimits the over- and under-parametrized regimes where fitting can or cannot be achieved. In the vicinity of this transition, properties of the curvature of the minima of the loss are critical. This transition shares direct similarities with the jamming transition by which particles form a disordered solid as the density is increased, which also occurs in certain classes of computational optimization and learning problems such as the perceptron. Our analysis gives a simple explanation as to why poor minima of the loss cannot be encountered in the overparametrized regime, and puts forward the surprising result that the ability of fully connected networks to fit random data is independent of their depth. Our observations suggests that this independence also holds for real data. We also study a quantity $\Delta$ which characterizes how well ($\Delta<0$) or badly ($\Delta>0$) a datum is learned. At the critical point it is power-law distributed, $P_+(\Delta)\sim\Delta^\theta$ for $\Delta>0$ and $P_-(\Delta)\sim(-\Delta)^{-\gamma}$ for $\Delta<0$, with $\theta\approx0.3$ and $\gamma\approx0.2$. This observation suggests that near the transition the loss landscape has a hierarchical structure and that the learning dynamics is prone to avalanche-like dynamics, with abrupt changes in the set of patterns that are learned.