The jamming transition as a paradigm to understand the loss landscape of deep neural networks
Paper and Code
Oct 03, 2018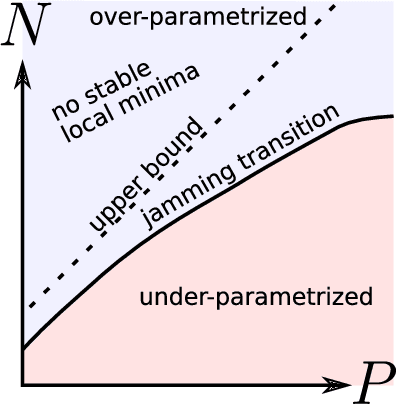
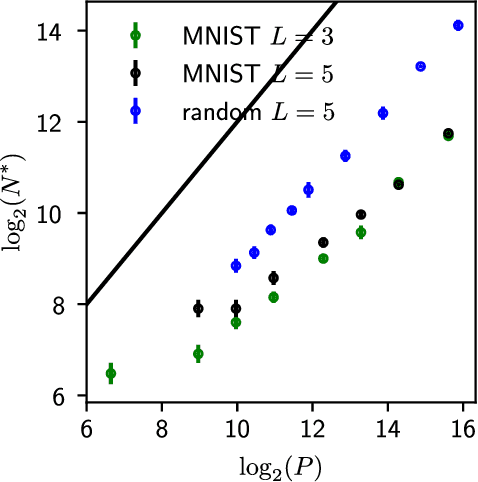
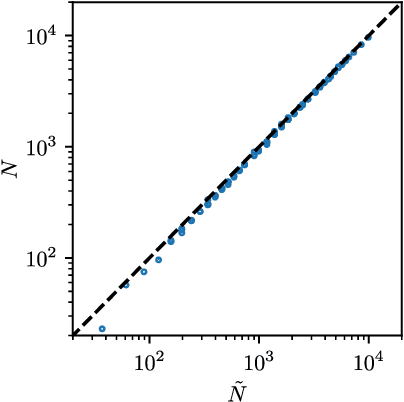
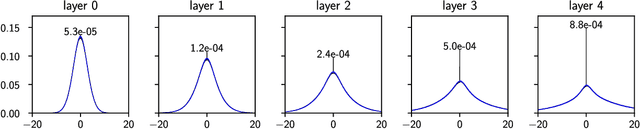
Deep learning has been immensely successful at a variety of tasks, ranging from classification to AI. Learning corresponds to fitting training data, which is implemented by descending a very high-dimensional loss function. Understanding under which conditions neural networks do not get stuck in poor minima of the loss, and how the landscape of that loss evolves as depth is increased remains a challenge. Here we predict, and test empirically, an analogy between this landscape and the energy landscape of repulsive ellipses. We argue that in FC networks a phase transition delimits the over- and under-parametrized regimes where fitting can or cannot be achieved. In the vicinity of this transition, properties of the curvature of the minima of the loss are critical. This transition shares direct similarities with the jamming transition by which particles form a disordered solid as the density is increased, which also occurs in certain classes of computational optimization and learning problems such as the perceptron. Our analysis gives a simple explanation as to why poor minima of the loss cannot be encountered in the overparametrized regime, and puts forward the surprising result that the ability of fully connected networks to fit random data is independent of their depth. Our observations suggests that this independence also holds for real data. We also study a quantity $\Delta$ which characterizes how well ($\Delta<0$) or badly ($\Delta>0$) a datum is learned. At the critical point it is power-law distributed, $P_+(\Delta)\sim\Delta^\theta$ for $\Delta>0$ and $P_-(\Delta)\sim(-\Delta)^{-\gamma}$ for $\Delta<0$, with $\theta\approx0.3$ and $\gamma\approx0.2$. This observation suggests that near the transition the loss landscape has a hierarchical structure and that the learning dynamics is prone to avalanche-like dynamics, with abrupt changes in the set of patterns that are learned.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge