How isotropic kernels learn simple invariants

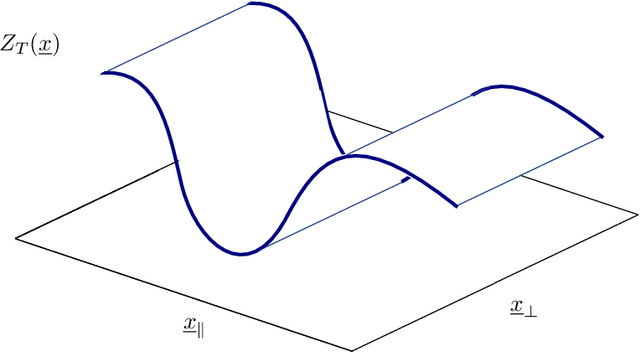
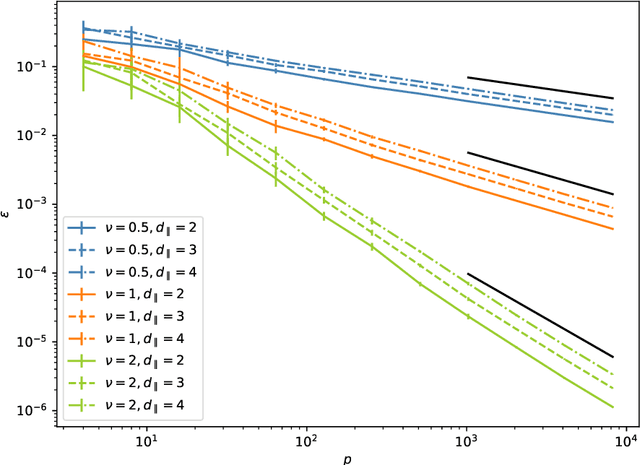
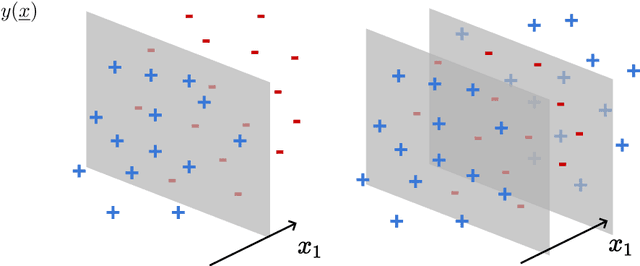
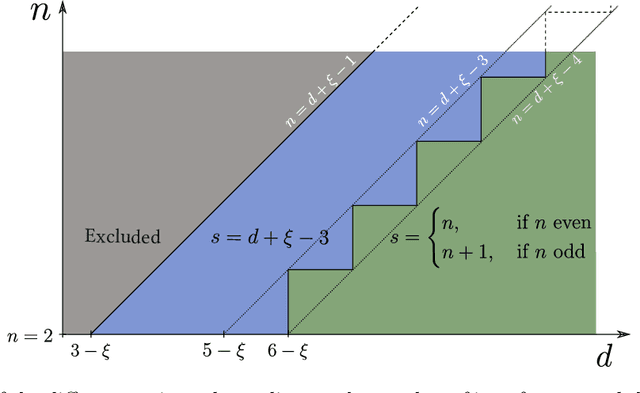
We investigate how the training curve of isotropic kernel methods depends on the symmetry of the task to be learned, in several settings. (i) We consider a regression task, where the target function is a Gaussian random field that depends only on $d_\parallel$ variables, fewer than the input dimension $d$. We compute the expected test error $\epsilon$ that follows $\epsilon\sim p^{-\beta}$ where $p$ is the size of the training set. We find that $\beta\sim\frac{1}{d}$ independently of $d_\parallel$, supporting previous findings that the presence of invariants does not resolve the curse of dimensionality for kernel regression. (ii) Next we consider support-vector binary classification and introduce the {\it stripe model} where the data label depends on a single coordinate $y(\underline x) = y(x_1)$, corresponding to parallel decision boundaries separating labels of different signs, and consider that there is no margin at these interfaces. We argue and confirm numerically that for large bandwidth, $\beta = \frac{d-1+\xi}{3d-3+\xi}$, where $\xi\in (0,2)$ is the exponent characterizing the singularity of the kernel at the origin. This estimation improves classical bounds obtainable from Rademacher complexity. In this setting there is no curse of dimensionality since $\beta\rightarrow\frac{1}{3}$ as $d\rightarrow\infty$. (iii) We confirm these findings for the {\it spherical model} for which $y(\underline x) = y(|\!|\underline x|\!|)$. (iv) In the stripe model, we show that if the data are compressed along their invariants by some factor $\lambda$ (an operation believed to take place in deep networks), the test error is reduced by a factor $\lambda^{-\frac{2(d-1)}{3d-3+\xi}}$.

Disentangling feature and lazy learning in deep neural networks: an empirical study

Two distinct limits for deep learning as the net width $h\to\infty$ have been proposed, depending on how the weights of the last layer scale with $h$. In the "lazy-learning" regime, the dynamics becomes linear in the weights and is described by a Neural Tangent Kernel $\Theta$. By contrast, in the "feature-learning" regime, the dynamics can be expressed in terms of the density distribution of the weights. Understanding which regime describes accurately practical architectures and which one leads to better performance remains a challenge. We answer these questions and produce new characterizations of these regimes for the MNIST data set, by considering deep nets $f$ whose last layer of weights scales as $\frac{\alpha}{\sqrt{h}}$ at initialization, where $\alpha$ is a parameter we vary. We performed systematic experiments on two setups (A) fully-connected Softplus momentum full batch and (B) convolutional ReLU momentum stochastic. We find that (1) $\alpha^*=\frac{1}{\sqrt{h}}$ separates the two regimes. (2) for (A) and (B) feature learning outperforms lazy learning, a difference in performance that decreases with $h$ and becomes hardly detectable asymptotically for (A) but is very significant for (B). (3) In both regimes, the fluctuations $\delta f$ induced by initial conditions on the learned function follow $\delta f\sim1/\sqrt{h}$, leading to a performance that increases with $h$. This improvement can be instead obtained at intermediate $h$ values by ensemble averaging different networks. (4) In the feature regime there exists a time scale $t_1\sim\alpha\sqrt{h}$, such that for $t\ll t_1$ the dynamics is linear. At $t\sim t_1$, the output has grown by a magnitude $\sqrt{h}$ and the changes of the tangent kernel $\|\Delta\Theta\|$ become significant. Ultimately, it follows $\|\Delta\Theta\|\sim(\sqrt{h}\alpha)^{-a}$ for ReLU and Softplus activation, with $a<2$ & $a\to2$ when depth grows.

Asymptotic learning curves of kernel methods: empirical data v.s. Teacher-Student paradigm

How many training data are needed to learn a supervised task? It is often observed that the generalization error decreases as $n^{-\beta}$ where $n$ is the number of training examples and $\beta$ an exponent that depends on both data and algorithm. In this work we measure $\beta$ when applying kernel methods to real datasets. For MNIST we find $\beta\approx 0.4$ and for CIFAR10 $\beta\approx 0.1$. Remarkably, $\beta$ is the same for regression and classification tasks, and for Gaussian or Laplace kernels. To rationalize the existence of non-trivial exponents that can be independent of the specific kernel used, we introduce the Teacher-Student framework for kernels. In this scheme, a Teacher generates data according to a Gaussian random field, and a Student learns them via kernel regression. With a simplifying assumption --- namely that the data are sampled from a regular lattice --- we derive analytically $\beta$ for translation invariant kernels, using previous results from the kriging literature. Provided that the Student is not too sensitive to high frequencies, $\beta$ depends only on the training data and their dimension. We confirm numerically that these predictions hold when the training points are sampled at random on a hypersphere. Overall, our results quantify how smooth Gaussian data should be to avoid the curse of dimensionality, and indicate that for kernel learning the relevant dimension of the data should be defined in terms of how the distance between nearest data points depends on $n$. With this definition one obtains reasonable effective smoothness estimates for MNIST and CIFAR10.

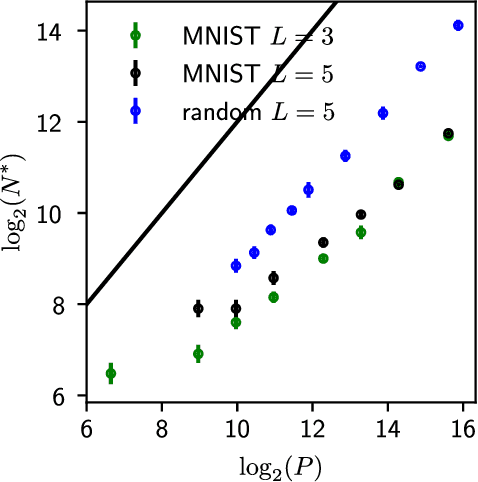
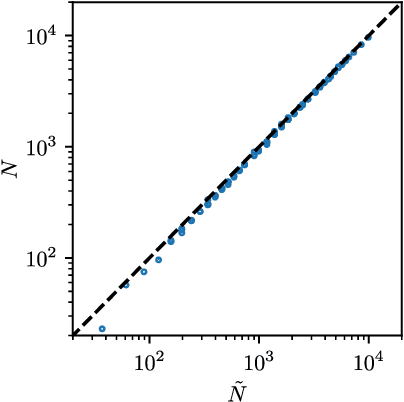
Scaling description of generalization with number of parameters in deep learning

We provide a description for the evolution of the generalization performance of fixed-depth fully-connected deep neural networks as a function of the number of parameters $N$. We observe that increasing $N$ at fixed depth reduces the fluctuations of the output function $f_N$ induced by initial conditions, with $\Vert f_N-{\bar f}_N\Vert\sim N^{-1/4}$ where ${\bar f}_N$ denotes an average over initial conditions, and we explain this asymptotic behavior in terms of the fluctuations of the so-called Neural Tangent Kernel that controls the dynamics of the output function. For the task of classification, we predict these fluctuations to increase the test error $\epsilon$ as $\epsilon_{N}-\epsilon_{\infty}\sim N^{-1/2} + \mathcal{O}( N^{-3/4})$: this prediction is consistent with our empirical results on the MNIST dataset and it explains the puzzling observation that the predictive power of deep networks improves as the number of fitting parameters grows. This asymptotic description breaks down at a so-called jamming transition which takes place at a critical $N=N^*$, below which the training error is non-zero. In the absence of regularization, we observe an apparent divergence $\Vert f_N\Vert\sim (N-N^*)^{-\alpha}$ and provide a simple argument suggesting $\alpha=1$, consistent with empirical observations. This result leads to a plausible explanation for the cusp in test error known to occur at $N^*$. In practice, our analysis suggests that optimal generalization can be reached by ensemble averaging output functions at $N$ fixed slightly above $N^*$.

A jamming transition from under- to over-parametrization affects loss landscape and generalization

We argue that in fully-connected networks a phase transition delimits the over- and under-parametrized regimes where fitting can or cannot be achieved. Under some general conditions, we show that this transition is sharp for the hinge loss. In the whole over-parametrized regime, poor minima of the loss are not encountered during training since the number of constraints to satisfy is too small to hamper minimization. Our findings support a link between this transition and the generalization properties of the network: as we increase the number of parameters of a given model, starting from an under-parametrized network, we observe that the generalization error displays three phases: (i) initial decay, (ii) increase until the transition point --- where it displays a cusp --- and (iii) power law decay toward a constant for the rest of the over-parametrized regime. Thereby we identify the region where the classical phenomenon of over-fitting takes place, and the region where the model keeps improving, in line with previous empirical observations for modern neural networks. The theoretical results presented here appeared elsewhere for a physics audience. The results on generalization are new.

The jamming transition as a paradigm to understand the loss landscape of deep neural networks

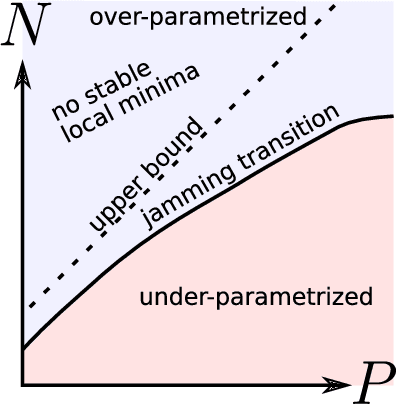
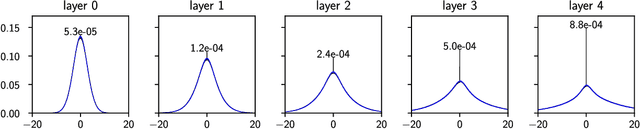
Deep learning has been immensely successful at a variety of tasks, ranging from classification to AI. Learning corresponds to fitting training data, which is implemented by descending a very high-dimensional loss function. Understanding under which conditions neural networks do not get stuck in poor minima of the loss, and how the landscape of that loss evolves as depth is increased remains a challenge. Here we predict, and test empirically, an analogy between this landscape and the energy landscape of repulsive ellipses. We argue that in FC networks a phase transition delimits the over- and under-parametrized regimes where fitting can or cannot be achieved. In the vicinity of this transition, properties of the curvature of the minima of the loss are critical. This transition shares direct similarities with the jamming transition by which particles form a disordered solid as the density is increased, which also occurs in certain classes of computational optimization and learning problems such as the perceptron. Our analysis gives a simple explanation as to why poor minima of the loss cannot be encountered in the overparametrized regime, and puts forward the surprising result that the ability of fully connected networks to fit random data is independent of their depth. Our observations suggests that this independence also holds for real data. We also study a quantity $\Delta$ which characterizes how well ($\Delta<0$) or badly ($\Delta>0$) a datum is learned. At the critical point it is power-law distributed, $P_+(\Delta)\sim\Delta^\theta$ for $\Delta>0$ and $P_-(\Delta)\sim(-\Delta)^{-\gamma}$ for $\Delta<0$, with $\theta\approx0.3$ and $\gamma\approx0.2$. This observation suggests that near the transition the loss landscape has a hierarchical structure and that the learning dynamics is prone to avalanche-like dynamics, with abrupt changes in the set of patterns that are learned.