How isotropic kernels learn simple invariants

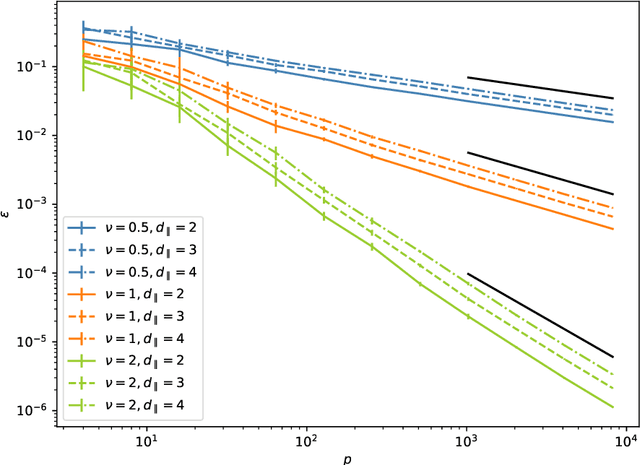
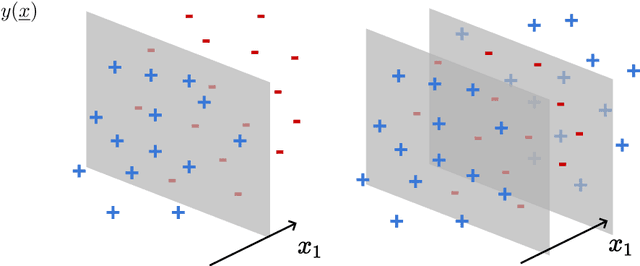
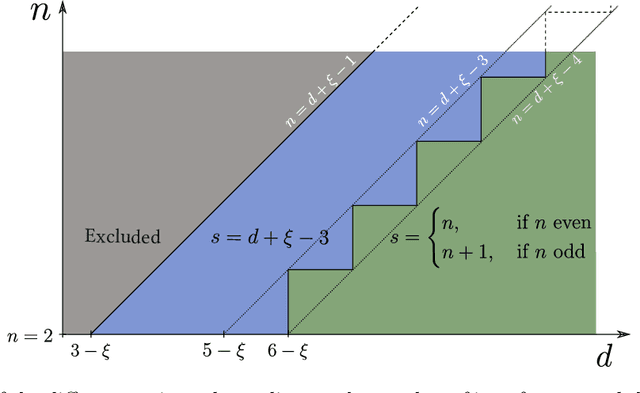
We investigate how the training curve of isotropic kernel methods depends on the symmetry of the task to be learned, in several settings. (i) We consider a regression task, where the target function is a Gaussian random field that depends only on $d_\parallel$ variables, fewer than the input dimension $d$. We compute the expected test error $\epsilon$ that follows $\epsilon\sim p^{-\beta}$ where $p$ is the size of the training set. We find that $\beta\sim\frac{1}{d}$ independently of $d_\parallel$, supporting previous findings that the presence of invariants does not resolve the curse of dimensionality for kernel regression. (ii) Next we consider support-vector binary classification and introduce the {\it stripe model} where the data label depends on a single coordinate $y(\underline x) = y(x_1)$, corresponding to parallel decision boundaries separating labels of different signs, and consider that there is no margin at these interfaces. We argue and confirm numerically that for large bandwidth, $\beta = \frac{d-1+\xi}{3d-3+\xi}$, where $\xi\in (0,2)$ is the exponent characterizing the singularity of the kernel at the origin. This estimation improves classical bounds obtainable from Rademacher complexity. In this setting there is no curse of dimensionality since $\beta\rightarrow\frac{1}{3}$ as $d\rightarrow\infty$. (iii) We confirm these findings for the {\it spherical model} for which $y(\underline x) = y(|\!|\underline x|\!|)$. (iv) In the stripe model, we show that if the data are compressed along their invariants by some factor $\lambda$ (an operation believed to take place in deep networks), the test error is reduced by a factor $\lambda^{-\frac{2(d-1)}{3d-3+\xi}}$.