Geometric compression of invariant manifolds in neural nets

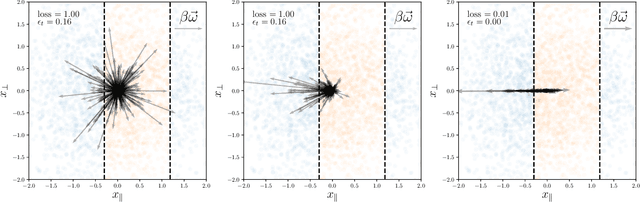
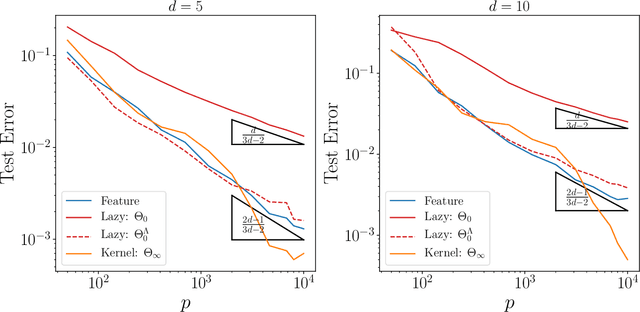
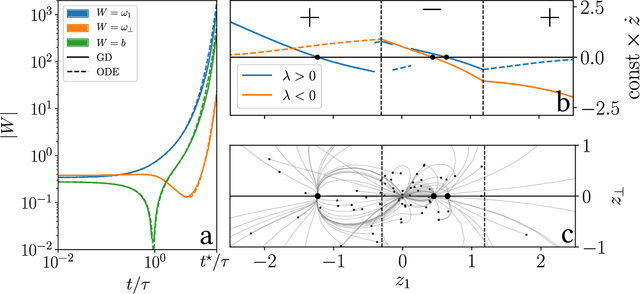
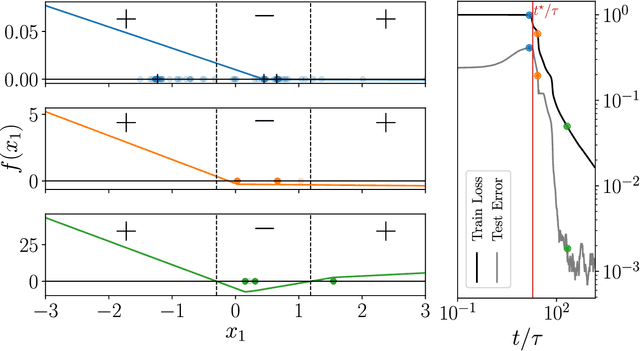
We study how neural networks compress uninformative input space in models where data lie in $d$ dimensions, but whose label only vary within a linear manifold of dimension $d_\parallel < d$. We show that for a one-hidden layer network initialized with infinitesimal weights (i.e. in the \textit{feature learning} regime) trained with gradient descent, the uninformative $d_\perp=d-d_\parallel$ space is compressed by a factor $\lambda\sim \sqrt{p}$, where $p$ is the size of the training set. We quantify the benefit of such a compression on the test error $\epsilon$. For large initialization of the weights (the \textit{lazy training} regime), no compression occurs and for regular boundaries separating labels we find that $\epsilon \sim p^{-\beta}$, with $\beta_\text{Lazy} = d / (3d-2)$. Compression improves the learning curves so that $\beta_\text{Feature} = (2d-1)/(3d-2)$ if $d_\parallel = 1$ and $\beta_\text{Feature} = (d + d_\perp/2)/(3d-2)$ if $d_\parallel > 1$. We test these predictions for a stripe model where boundaries are parallel interfaces ($d_\parallel=1$) as well as for a cylindrical boundary ($d_\parallel=2$). Next we show that compression shapes the Neural Tangent Kernel (NTK) evolution in time, so that its top eigenvectors become more informative and display a larger projection on the labels. Consequently, kernel learning with the frozen NTK at the end of training outperforms the initial NTK. We confirm these predictions both for a one-hidden layer FC network trained on the stripe model and for a 16-layers CNN trained on MNIST, for which we also find $\beta_\text{Feature}>\beta_\text{Lazy}$. The great similarities found in these two cases support that compression is central to the training of MNIST, and puts forward kernel-PCA on the evolving NTK as a useful diagnostic of compression in deep nets.

How isotropic kernels learn simple invariants

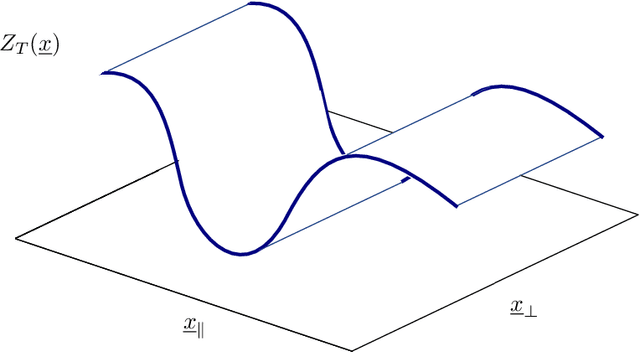
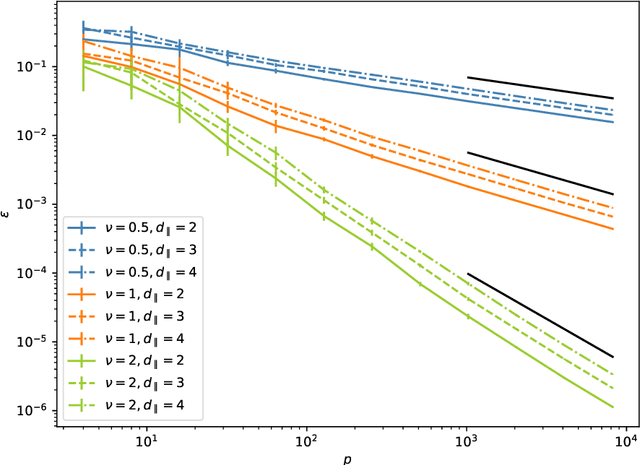
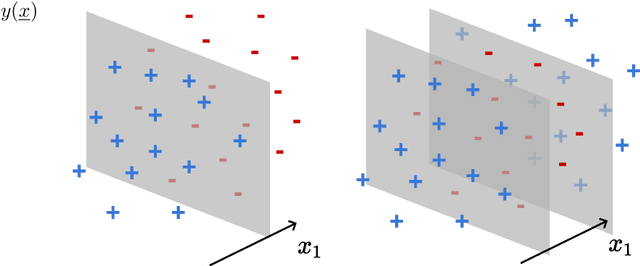
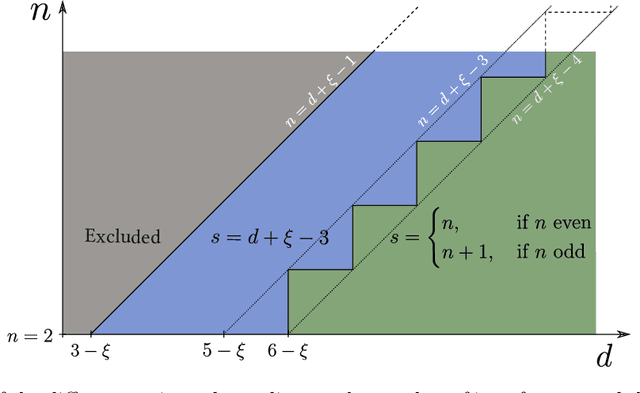
We investigate how the training curve of isotropic kernel methods depends on the symmetry of the task to be learned, in several settings. (i) We consider a regression task, where the target function is a Gaussian random field that depends only on $d_\parallel$ variables, fewer than the input dimension $d$. We compute the expected test error $\epsilon$ that follows $\epsilon\sim p^{-\beta}$ where $p$ is the size of the training set. We find that $\beta\sim\frac{1}{d}$ independently of $d_\parallel$, supporting previous findings that the presence of invariants does not resolve the curse of dimensionality for kernel regression. (ii) Next we consider support-vector binary classification and introduce the {\it stripe model} where the data label depends on a single coordinate $y(\underline x) = y(x_1)$, corresponding to parallel decision boundaries separating labels of different signs, and consider that there is no margin at these interfaces. We argue and confirm numerically that for large bandwidth, $\beta = \frac{d-1+\xi}{3d-3+\xi}$, where $\xi\in (0,2)$ is the exponent characterizing the singularity of the kernel at the origin. This estimation improves classical bounds obtainable from Rademacher complexity. In this setting there is no curse of dimensionality since $\beta\rightarrow\frac{1}{3}$ as $d\rightarrow\infty$. (iii) We confirm these findings for the {\it spherical model} for which $y(\underline x) = y(|\!|\underline x|\!|)$. (iv) In the stripe model, we show that if the data are compressed along their invariants by some factor $\lambda$ (an operation believed to take place in deep networks), the test error is reduced by a factor $\lambda^{-\frac{2(d-1)}{3d-3+\xi}}$.