When the Left Foot Leads to the Right Path: Bridging Initial Prejudice and Trainability

Understanding the statistical properties of deep neural networks (DNNs) at initialization is crucial for elucidating both their trainability and the intrinsic architectural biases they encode prior to data exposure. Mean-field (MF) analyses have demonstrated that the parameter distribution in randomly initialized networks dictates whether gradients vanish or explode. Concurrently, untrained DNNs were found to exhibit an initial-guessing bias (IGB), in which large regions of the input space are assigned to a single class. In this work, we derive a theoretical proof establishing the correspondence between IGB and previous MF theories, thereby connecting a network prejudice toward specific classes with the conditions for fast and accurate learning. This connection yields the counter-intuitive conclusion: the initialization that optimizes trainability is necessarily biased, rather than neutral. Furthermore, we extend the MF/IGB framework to multi-node activation functions, offering practical guidelines for designing initialization schemes that ensure stable optimization in architectures employing max- and average-pooling layers.

Where You Place the Norm Matters: From Prejudiced to Neutral Initializations

Normalization layers, such as Batch Normalization and Layer Normalization, are central components in modern neural networks, widely adopted to improve training stability and generalization. While their practical effectiveness is well documented, a detailed theoretical understanding of how normalization affects model behavior, starting from initialization, remains an important open question. In this work, we investigate how both the presence and placement of normalization within hidden layers influence the statistical properties of network predictions before training begins. In particular, we study how these choices shape the distribution of class predictions at initialization, which can range from unbiased (Neutral) to highly concentrated (Prejudiced) toward a subset of classes. Our analysis shows that normalization placement induces systematic differences in the initial prediction behavior of neural networks, which in turn shape the dynamics of learning. By linking architectural choices to prediction statistics at initialization, our work provides a principled understanding of how normalization can influence early training behavior and offers guidance for more controlled and interpretable network design.

Unbiased and Sign Compression in Distributed Learning: Comparing Noise Resilience via SDEs

Distributed methods are essential for handling machine learning pipelines comprising large-scale models and datasets. However, their benefits often come at the cost of increased communication overhead between the central server and agents, which can become the main bottleneck, making training costly or even unfeasible in such systems. Compression methods such as quantization and sparsification can alleviate this issue. Still, their robustness to large and heavy-tailed gradient noise, a phenomenon sometimes observed in language modeling, remains poorly understood. This work addresses this gap by analyzing Distributed Compressed SGD (DCSGD) and Distributed SignSGD (DSignSGD) using stochastic differential equations (SDEs). Our results show that DCSGD with unbiased compression is more vulnerable to noise in stochastic gradients, while DSignSGD remains robust, even under large and heavy-tailed noise. Additionally, we propose new scaling rules for hyperparameter tuning to mitigate performance degradation due to compression. These findings are empirically validated across multiple deep learning architectures and datasets, providing practical recommendations for distributed optimization.

Double Momentum and Error Feedback for Clipping with Fast Rates and Differential Privacy

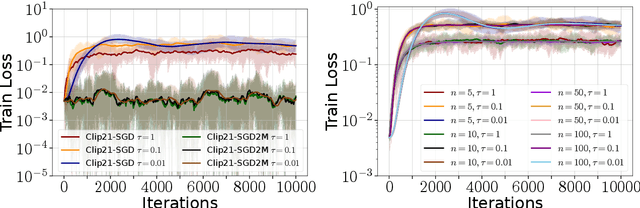
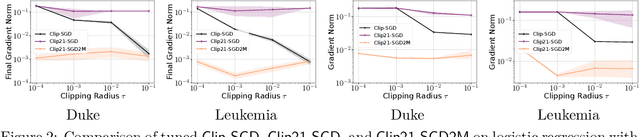
Strong Differential Privacy (DP) and Optimization guarantees are two desirable properties for a method in Federated Learning (FL). However, existing algorithms do not achieve both properties at once: they either have optimal DP guarantees but rely on restrictive assumptions such as bounded gradients/bounded data heterogeneity, or they ensure strong optimization performance but lack DP guarantees. To address this gap in the literature, we propose and analyze a new method called Clip21-SGD2M based on a novel combination of clipping, heavy-ball momentum, and Error Feedback. In particular, for non-convex smooth distributed problems with clients having arbitrarily heterogeneous data, we prove that Clip21-SGD2M has optimal convergence rate and also near optimal (local-)DP neighborhood. Our numerical experiments on non-convex logistic regression and training of neural networks highlight the superiority of Clip21-SGD2M over baselines in terms of the optimization performance for a given DP-budget.

Adaptive Methods through the Lens of SDEs: Theoretical Insights on the Role of Noise

Despite the vast empirical evidence supporting the efficacy of adaptive optimization methods in deep learning, their theoretical understanding is far from complete. This work introduces novel SDEs for commonly used adaptive optimizers: SignSGD, RMSprop(W), and Adam(W). These SDEs offer a quantitatively accurate description of these optimizers and help illuminate an intricate relationship between adaptivity, gradient noise, and curvature. Our novel analysis of SignSGD highlights a noteworthy and precise contrast to SGD in terms of convergence speed, stationary distribution, and robustness to heavy-tail noise. We extend this analysis to AdamW and RMSpropW, for which we observe that the role of noise is much more complex. Crucially, we support our theoretical analysis with experimental evidence by verifying our insights: this includes numerically integrating our SDEs using Euler-Maruyama discretization on various neural network architectures such as MLPs, CNNs, ResNets, and Transformers. Our SDEs accurately track the behavior of the respective optimizers, especially when compared to previous SDEs derived for Adam and RMSprop. We believe our approach can provide valuable insights into best training practices and novel scaling rules.

Theoretical characterisation of the Gauss-Newton conditioning in Neural Networks

The Gauss-Newton (GN) matrix plays an important role in machine learning, most evident in its use as a preconditioning matrix for a wide family of popular adaptive methods to speed up optimization. Besides, it can also provide key insights into the optimization landscape of neural networks. In the context of deep neural networks, understanding the GN matrix involves studying the interaction between different weight matrices as well as the dependencies introduced by the data, thus rendering its analysis challenging. In this work, we take a first step towards theoretically characterizing the conditioning of the GN matrix in neural networks. We establish tight bounds on the condition number of the GN in deep linear networks of arbitrary depth and width, which we also extend to two-layer ReLU networks. We expand the analysis to further architectural components, such as residual connections and convolutional layers. Finally, we empirically validate the bounds and uncover valuable insights into the influence of the analyzed architectural components.

A Comprehensive Analysis on the Learning Curve in Kernel Ridge Regression

This paper conducts a comprehensive study of the learning curves of kernel ridge regression (KRR) under minimal assumptions. Our contributions are three-fold: 1) we analyze the role of key properties of the kernel, such as its spectral eigen-decay, the characteristics of the eigenfunctions, and the smoothness of the kernel; 2) we demonstrate the validity of the Gaussian Equivalent Property (GEP), which states that the generalization performance of KRR remains the same when the whitened features are replaced by standard Gaussian vectors, thereby shedding light on the success of previous analyzes under the Gaussian Design Assumption; 3) we derive novel bounds that improve over existing bounds across a broad range of setting such as (in)dependent feature vectors and various combinations of eigen-decay rates in the over/underparameterized regimes.

Loss Landscape Characterization of Neural Networks without Over-Parametrization

Optimization methods play a crucial role in modern machine learning, powering the remarkable empirical achievements of deep learning models. These successes are even more remarkable given the complex non-convex nature of the loss landscape of these models. Yet, ensuring the convergence of optimization methods requires specific structural conditions on the objective function that are rarely satisfied in practice. One prominent example is the widely recognized Polyak-Lojasiewicz (PL) inequality, which has gained considerable attention in recent years. However, validating such assumptions for deep neural networks entails substantial and often impractical levels of over-parametrization. In order to address this limitation, we propose a novel class of functions that can characterize the loss landscape of modern deep models without requiring extensive over-parametrization and can also include saddle points. Crucially, we prove that gradient-based optimizers possess theoretical guarantees of convergence under this assumption. Finally, we validate the soundness of our new function class through both theoretical analysis and empirical experimentation across a diverse range of deep learning models.

Cubic regularized subspace Newton for non-convex optimization

This paper addresses the optimization problem of minimizing non-convex continuous functions, which is relevant in the context of high-dimensional machine learning applications characterized by over-parametrization. We analyze a randomized coordinate second-order method named SSCN which can be interpreted as applying cubic regularization in random subspaces. This approach effectively reduces the computational complexity associated with utilizing second-order information, rendering it applicable in higher-dimensional scenarios. Theoretically, we establish convergence guarantees for non-convex functions, with interpolating rates for arbitrary subspace sizes and allowing inexact curvature estimation. When increasing subspace size, our complexity matches $\mathcal{O}(\epsilon^{-3/2})$ of the cubic regularization (CR) rate. Additionally, we propose an adaptive sampling scheme ensuring exact convergence rate of $\mathcal{O}(\epsilon^{-3/2}, \epsilon^{-3})$ to a second-order stationary point, even without sampling all coordinates. Experimental results demonstrate substantial speed-ups achieved by SSCN compared to conventional first-order methods.

SDEs for Minimax Optimization

Minimax optimization problems have attracted a lot of attention over the past few years, with applications ranging from economics to machine learning. While advanced optimization methods exist for such problems, characterizing their dynamics in stochastic scenarios remains notably challenging. In this paper, we pioneer the use of stochastic differential equations (SDEs) to analyze and compare Minimax optimizers. Our SDE models for Stochastic Gradient Descent-Ascent, Stochastic Extragradient, and Stochastic Hamiltonian Gradient Descent are provable approximations of their algorithmic counterparts, clearly showcasing the interplay between hyperparameters, implicit regularization, and implicit curvature-induced noise. This perspective also allows for a unified and simplified analysis strategy based on the principles of It\^o calculus. Finally, our approach facilitates the derivation of convergence conditions and closed-form solutions for the dynamics in simplified settings, unveiling further insights into the behavior of different optimizers.