Convergence of Clipped-SGD for Convex $(L_0,L_1)$-Smooth Optimization with Heavy-Tailed Noise

Gradient clipping is a widely used technique in Machine Learning and Deep Learning (DL), known for its effectiveness in mitigating the impact of heavy-tailed noise, which frequently arises in the training of large language models. Additionally, first-order methods with clipping, such as Clip-SGD, exhibit stronger convergence guarantees than SGD under the $(L_0,L_1)$-smoothness assumption, a property observed in many DL tasks. However, the high-probability convergence of Clip-SGD under both assumptions -- heavy-tailed noise and $(L_0,L_1)$-smoothness -- has not been fully addressed in the literature. In this paper, we bridge this critical gap by establishing the first high-probability convergence bounds for Clip-SGD applied to convex $(L_0,L_1)$-smooth optimization with heavy-tailed noise. Our analysis extends prior results by recovering known bounds for the deterministic case and the stochastic setting with $L_1 = 0$ as special cases. Notably, our rates avoid exponentially large factors and do not rely on restrictive sub-Gaussian noise assumptions, significantly broadening the applicability of gradient clipping.

Double Momentum and Error Feedback for Clipping with Fast Rates and Differential Privacy

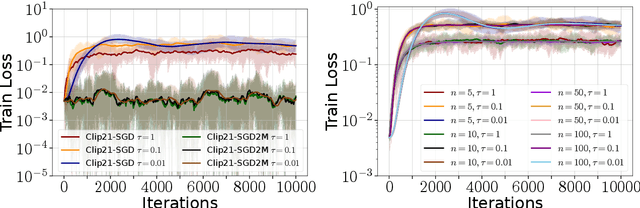
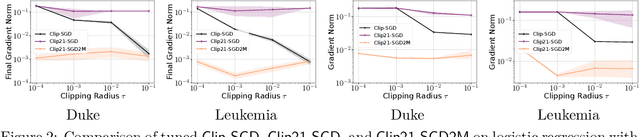
Strong Differential Privacy (DP) and Optimization guarantees are two desirable properties for a method in Federated Learning (FL). However, existing algorithms do not achieve both properties at once: they either have optimal DP guarantees but rely on restrictive assumptions such as bounded gradients/bounded data heterogeneity, or they ensure strong optimization performance but lack DP guarantees. To address this gap in the literature, we propose and analyze a new method called Clip21-SGD2M based on a novel combination of clipping, heavy-ball momentum, and Error Feedback. In particular, for non-convex smooth distributed problems with clients having arbitrarily heterogeneous data, we prove that Clip21-SGD2M has optimal convergence rate and also near optimal (local-)DP neighborhood. Our numerical experiments on non-convex logistic regression and training of neural networks highlight the superiority of Clip21-SGD2M over baselines in terms of the optimization performance for a given DP-budget.

Methods with Local Steps and Random Reshuffling for Generally Smooth Non-Convex Federated Optimization

Non-convex Machine Learning problems typically do not adhere to the standard smoothness assumption. Based on empirical findings, Zhang et al. (2020b) proposed a more realistic generalized $(L_0, L_1)$-smoothness assumption, though it remains largely unexplored. Many existing algorithms designed for standard smooth problems need to be revised. However, in the context of Federated Learning, only a few works address this problem but rely on additional limiting assumptions. In this paper, we address this gap in the literature: we propose and analyze new methods with local steps, partial participation of clients, and Random Reshuffling without extra restrictive assumptions beyond generalized smoothness. The proposed methods are based on the proper interplay between clients' and server's stepsizes and gradient clipping. Furthermore, we perform the first analysis of these methods under the Polyak-{\L} ojasiewicz condition. Our theory is consistent with the known results for standard smooth problems, and our experimental results support the theoretical insights.

Initialization using Update Approximation is a Silver Bullet for Extremely Efficient Low-Rank Fine-Tuning

Low-rank adapters have become a standard approach for efficiently fine-tuning large language models (LLMs), but they often fall short of achieving the performance of full fine-tuning. We propose a method, LoRA Silver Bullet or LoRA-SB, that approximates full fine-tuning within low-rank subspaces using a carefully designed initialization strategy. We theoretically demonstrate that the architecture of LoRA-XS, which inserts a trainable (r x r) matrix between B and A while keeping other matrices fixed, provides the precise conditions needed for this approximation. We leverage its constrained update space to achieve optimal scaling for high-rank gradient updates while removing the need for hyperparameter tuning. We prove that our initialization offers an optimal low-rank approximation of the initial gradient and preserves update directions throughout training. Extensive experiments across mathematical reasoning, commonsense reasoning, and language understanding tasks demonstrate that our approach exceeds the performance of standard LoRA while using 27-90x fewer parameters, and comprehensively outperforms LoRA-XS. Our findings establish that it is possible to simulate full fine-tuning in low-rank subspaces, and achieve significant efficiency gains without sacrificing performance. Our code is publicly available at https://github.com/RaghavSinghal10/lora-sb.

Error Feedback under $(L_0,L_1)$-Smoothness: Normalization and Momentum

We provide the first proof of convergence for normalized error feedback algorithms across a wide range of machine learning problems. Despite their popularity and efficiency in training deep neural networks, traditional analyses of error feedback algorithms rely on the smoothness assumption that does not capture the properties of objective functions in these problems. Rather, these problems have recently been shown to satisfy generalized smoothness assumptions, and the theoretical understanding of error feedback algorithms under these assumptions remains largely unexplored. Moreover, to the best of our knowledge, all existing analyses under generalized smoothness either i) focus on single-node settings or ii) make unrealistically strong assumptions for distributed settings, such as requiring data heterogeneity, and almost surely bounded stochastic gradient noise variance. In this paper, we propose distributed error feedback algorithms that utilize normalization to achieve the $O(1/\sqrt{K})$ convergence rate for nonconvex problems under generalized smoothness. Our analyses apply for distributed settings without data heterogeneity conditions, and enable stepsize tuning that is independent of problem parameters. Additionally, we provide strong convergence guarantees of normalized error feedback algorithms for stochastic settings. Finally, we show that due to their larger allowable stepsizes, our new normalized error feedback algorithms outperform their non-normalized counterparts on various tasks, including the minimization of polynomial functions, logistic regression, and ResNet-20 training.

Low-Resource Machine Translation through the Lens of Personalized Federated Learning

We present a new approach based on the Personalized Federated Learning algorithm MeritFed that can be applied to Natural Language Tasks with heterogeneous data. We evaluate it on the Low-Resource Machine Translation task, using the dataset from the Large-Scale Multilingual Machine Translation Shared Task (Small Track #2) and the subset of Sami languages from the multilingual benchmark for Finno-Ugric languages. In addition to its effectiveness, MeritFed is also highly interpretable, as it can be applied to track the impact of each language used for training. Our analysis reveals that target dataset size affects weight distribution across auxiliary languages, that unrelated languages do not interfere with the training, and auxiliary optimizer parameters have minimal impact. Our approach is easy to apply with a few lines of code, and we provide scripts for reproducing the experiments at https://github.com/VityaVitalich/MeritFed

Gradient Clipping Improves AdaGrad when the Noise Is Heavy-Tailed

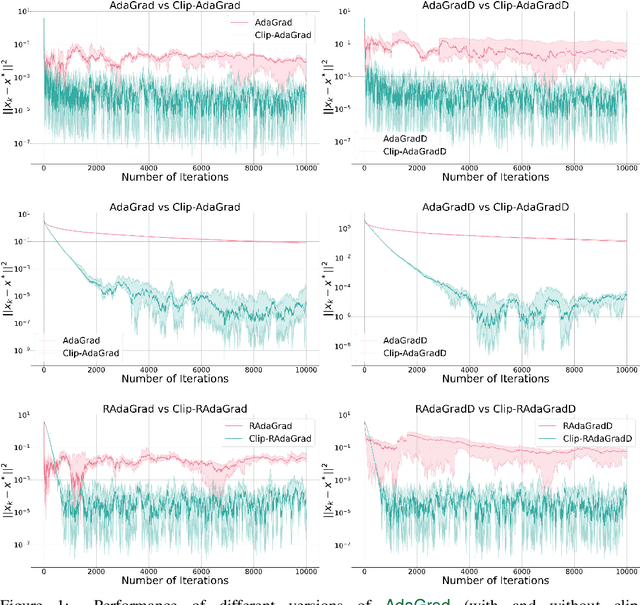
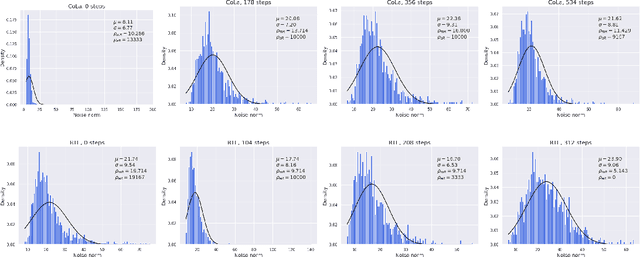
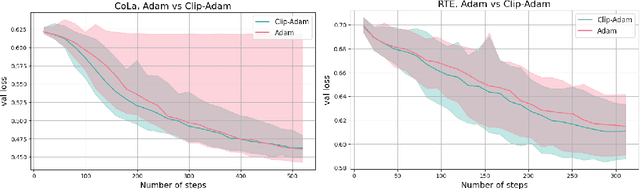
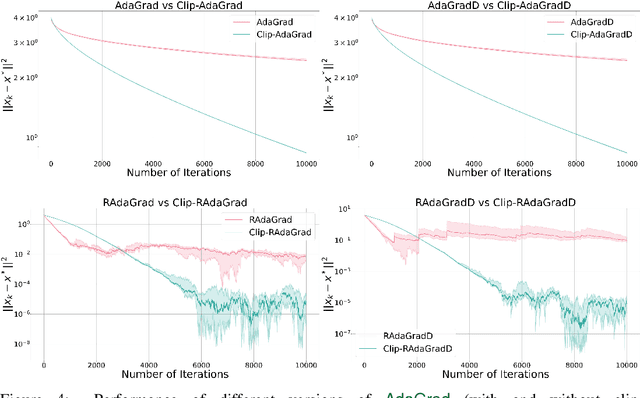
Methods with adaptive stepsizes, such as AdaGrad and Adam, are essential for training modern Deep Learning models, especially Large Language Models. Typically, the noise in the stochastic gradients is heavy-tailed for the later ones. Gradient clipping provably helps to achieve good high-probability convergence for such noises. However, despite the similarity between AdaGrad/Adam and Clip-SGD, the high-probability convergence of AdaGrad/Adam has not been studied in this case. In this work, we prove that AdaGrad (and its delayed version) can have provably bad high-probability convergence if the noise is heavy-tailed. To fix this issue, we propose a new version of AdaGrad called Clip-RAdaGradD (Clipped Reweighted AdaGrad with Delay) and prove its high-probability convergence bounds with polylogarithmic dependence on the confidence level for smooth convex/non-convex stochastic optimization with heavy-tailed noise. Our empirical evaluations, including NLP model fine-tuning, highlight the superiority of clipped versions of AdaGrad/Adam in handling the heavy-tailed noise.

Remove that Square Root: A New Efficient Scale-Invariant Version of AdaGrad

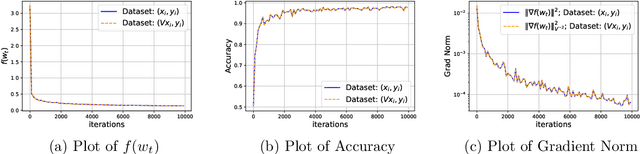
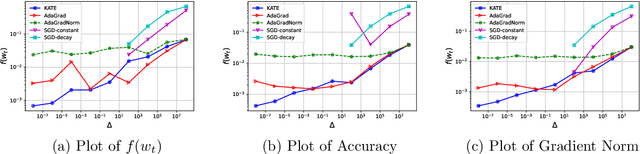
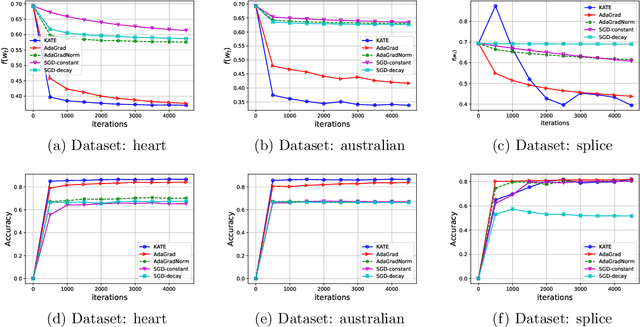
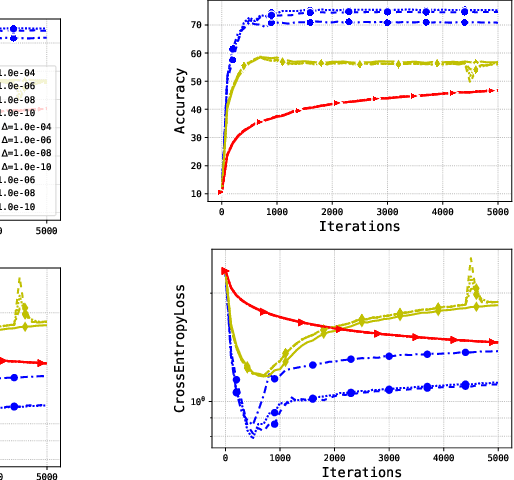
Adaptive methods are extremely popular in machine learning as they make learning rate tuning less expensive. This paper introduces a novel optimization algorithm named KATE, which presents a scale-invariant adaptation of the well-known AdaGrad algorithm. We prove the scale-invariance of KATE for the case of Generalized Linear Models. Moreover, for general smooth non-convex problems, we establish a convergence rate of $O \left(\frac{\log T}{\sqrt{T}} \right)$ for KATE, matching the best-known ones for AdaGrad and Adam. We also compare KATE to other state-of-the-art adaptive algorithms Adam and AdaGrad in numerical experiments with different problems, including complex machine learning tasks like image classification and text classification on real data. The results indicate that KATE consistently outperforms AdaGrad and matches/surpasses the performance of Adam in all considered scenarios.

Federated Learning Can Find Friends That Are Beneficial

In Federated Learning (FL), the distributed nature and heterogeneity of client data present both opportunities and challenges. While collaboration among clients can significantly enhance the learning process, not all collaborations are beneficial; some may even be detrimental. In this study, we introduce a novel algorithm that assigns adaptive aggregation weights to clients participating in FL training, identifying those with data distributions most conducive to a specific learning objective. We demonstrate that our aggregation method converges no worse than the method that aggregates only the updates received from clients with the same data distribution. Furthermore, empirical evaluations consistently reveal that collaborations guided by our algorithm outperform traditional FL approaches. This underscores the critical role of judicious client selection and lays the foundation for more streamlined and effective FL implementations in the coming years.

Byzantine Robustness and Partial Participation Can Be Achieved Simultaneously: Just Clip Gradient Differences

Distributed learning has emerged as a leading paradigm for training large machine learning models. However, in real-world scenarios, participants may be unreliable or malicious, posing a significant challenge to the integrity and accuracy of the trained models. Byzantine fault tolerance mechanisms have been proposed to address these issues, but they often assume full participation from all clients, which is not always practical due to the unavailability of some clients or communication constraints. In our work, we propose the first distributed method with client sampling and provable tolerance to Byzantine workers. The key idea behind the developed method is the use of gradient clipping to control stochastic gradient differences in recursive variance reduction. This allows us to bound the potential harm caused by Byzantine workers, even during iterations when all sampled clients are Byzantine. Furthermore, we incorporate communication compression into the method to enhance communication efficiency. Under quite general assumptions, we prove convergence rates for the proposed method that match the existing state-of-the-art (SOTA) theoretical results.