Methods with Local Steps and Random Reshuffling for Generally Smooth Non-Convex Federated Optimization

Non-convex Machine Learning problems typically do not adhere to the standard smoothness assumption. Based on empirical findings, Zhang et al. (2020b) proposed a more realistic generalized $(L_0, L_1)$-smoothness assumption, though it remains largely unexplored. Many existing algorithms designed for standard smooth problems need to be revised. However, in the context of Federated Learning, only a few works address this problem but rely on additional limiting assumptions. In this paper, we address this gap in the literature: we propose and analyze new methods with local steps, partial participation of clients, and Random Reshuffling without extra restrictive assumptions beyond generalized smoothness. The proposed methods are based on the proper interplay between clients' and server's stepsizes and gradient clipping. Furthermore, we perform the first analysis of these methods under the Polyak-{\L} ojasiewicz condition. Our theory is consistent with the known results for standard smooth problems, and our experimental results support the theoretical insights.

AdaBatchGrad: Combining Adaptive Batch Size and Adaptive Step Size

This paper presents a novel adaptation of the Stochastic Gradient Descent (SGD), termed AdaBatchGrad. This modification seamlessly integrates an adaptive step size with an adjustable batch size. An increase in batch size and a decrease in step size are well-known techniques to tighten the area of convergence of SGD and decrease its variance. A range of studies by R. Byrd and J. Nocedal introduced various testing techniques to assess the quality of mini-batch gradient approximations and choose the appropriate batch sizes at every step. Methods that utilized exact tests were observed to converge within $O(LR^2/\varepsilon)$ iterations. Conversely, inexact test implementations sometimes resulted in non-convergence and erratic performance. To address these challenges, AdaBatchGrad incorporates both adaptive batch and step sizes, enhancing the method's robustness and stability. For exact tests, our approach converges in $O(LR^2/\varepsilon)$ iterations, analogous to standard gradient descent. For inexact tests, it achieves convergence in $O(\max\lbrace LR^2/\varepsilon, \sigma^2 R^2/\varepsilon^2 \rbrace )$ iterations. This makes AdaBatchGrad markedly more robust and computationally efficient relative to prevailing methods. To substantiate the efficacy of our method, we experimentally show, how the introduction of adaptive step size and adaptive batch size gradually improves the performance of regular SGD. The results imply that AdaBatchGrad surpasses alternative methods, especially when applied to inexact tests.

Self-concordant analysis of Frank-Wolfe algorithms

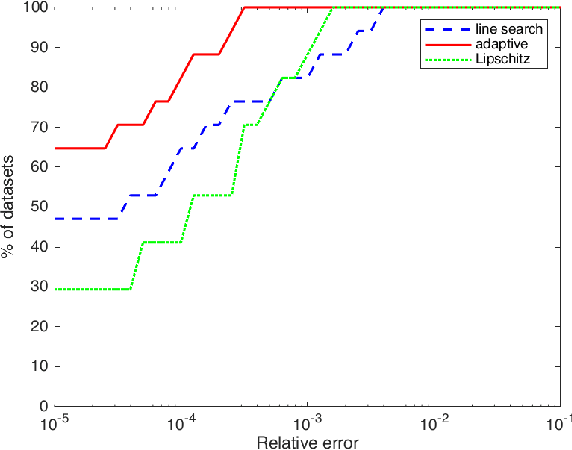
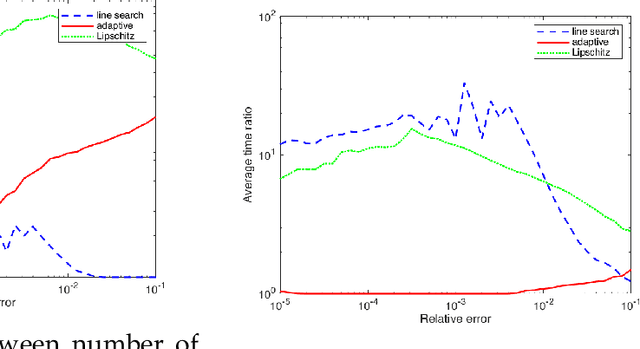
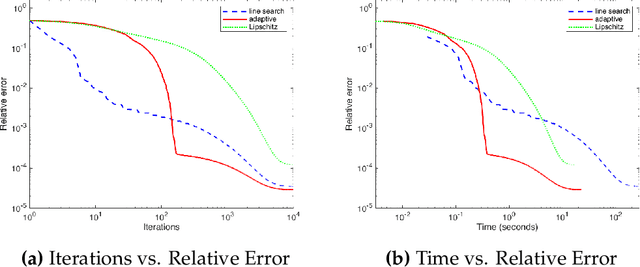
Projection-free optimization via different variants of the Frank-Wolfe (FW) method has become one of the cornerstones in optimization for machine learning since in many cases the linear minimization oracle is much cheaper to implement than projections and some sparsity needs to be preserved. In a number of applications, e.g. Poisson inverse problems or quantum state tomography, the loss is given by a self-concordant (SC) function having unbounded curvature, implying absence of theoretical guarantees for the existing FW methods. We use the theory of SC functions to provide a new adaptive step size for FW methods and prove global convergence rate O(1/k), k being the iteration counter. If the problem can be represented by a local linear minimization oracle, we are the first to propose a FW method with linear convergence rate without assuming neither strong convexity nor a Lipschitz continuous gradient.