An Online Feasible Point Method for Benign Generalized Nash Equilibrium Problems

We consider a repeatedly played generalized Nash equilibrium game. This induces a multi-agent online learning problem with joint constraints. An important challenge in this setting is that the feasible set for each agent depends on the simultaneous moves of the other agents and, therefore, varies over time. As a consequence, the agents face time-varying constraints, which are not adversarial but rather endogenous to the system. Prior work in this setting focused on convergence to a feasible solution in the limit via integrating the constraints in the objective as a penalty function. However, no existing work can guarantee that the constraints are satisfied for all iterations while simultaneously guaranteeing convergence to a generalized Nash equilibrium. This is a problem of fundamental theoretical interest and practical relevance. In this work, we introduce a new online feasible point method. Under the assumption that limited communication between the agents is allowed, this method guarantees feasibility. We identify the class of benign generalized Nash equilibrium problems, for which the convergence of our method to the equilibrium is guaranteed. We set this class of benign generalized Nash equilibrium games in context with existing definitions and illustrate our method with examples.

A conditional gradient homotopy method with applications to Semidefinite Programming

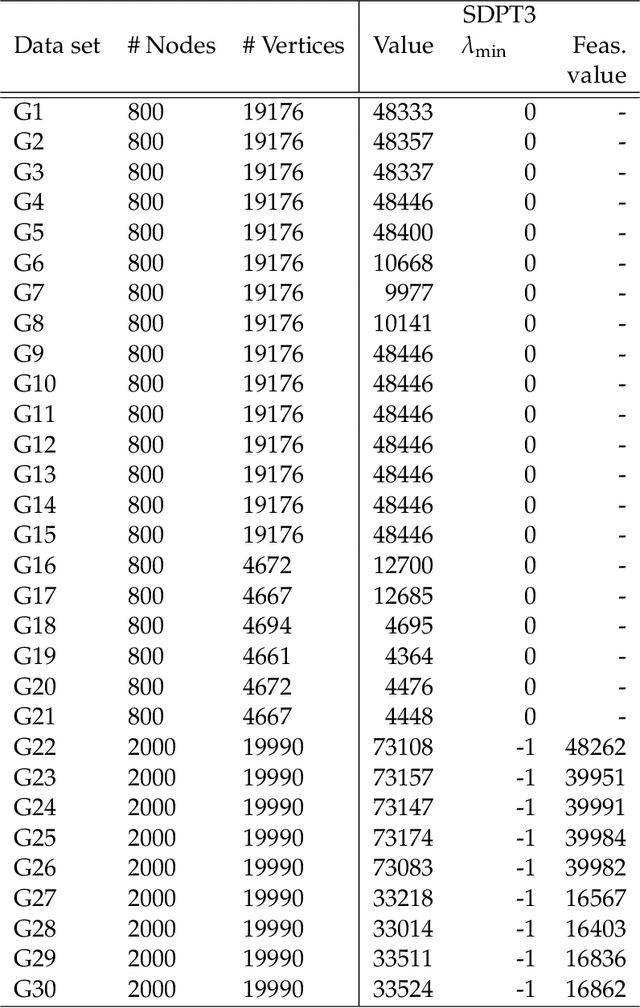
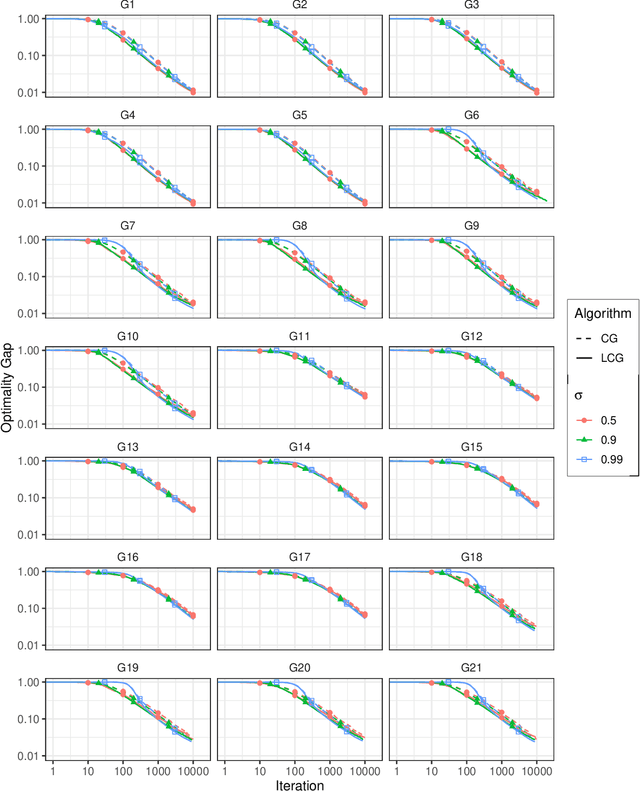
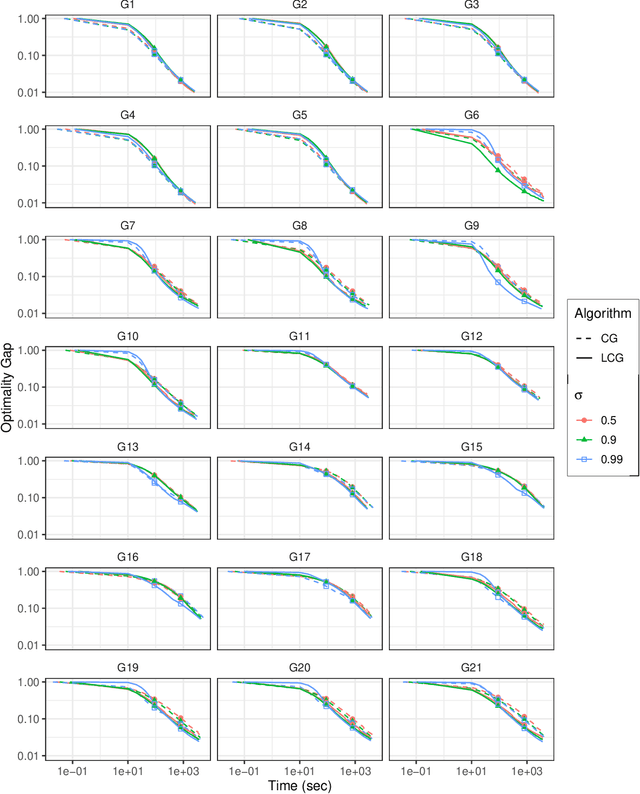
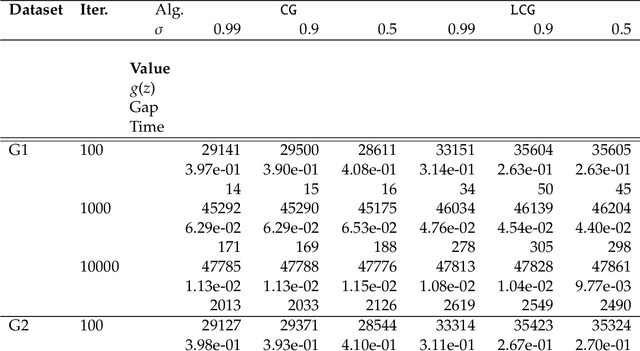
We propose a new homotopy-based conditional gradient method for solving convex optimization problems with a large number of simple conic constraints. Instances of this template naturally appear in semidefinite programming problems arising as convex relaxations of combinatorial optimization problems. Our method is a double-loop algorithm in which the conic constraint is treated via a self-concordant barrier, and the inner loop employs a conditional gradient algorithm to approximate the analytic central path, while the outer loop updates the accuracy imposed on the temporal solution and the homotopy parameter. Our theoretical iteration complexity is competitive when confronted to state-of-the-art SDP solvers, with the decisive advantage of cheap projection-free subroutines. Preliminary numerical experiments are provided for illustrating the practical performance of the method.

First-Order Methods for Convex Optimization

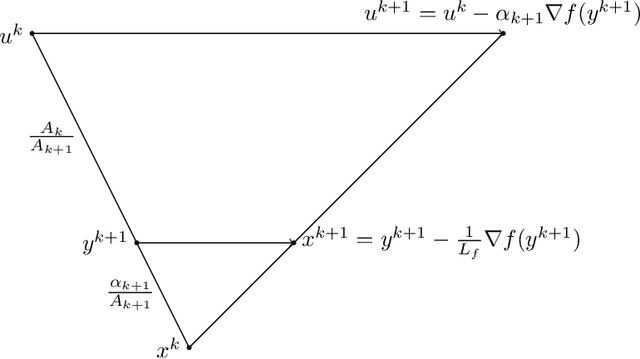
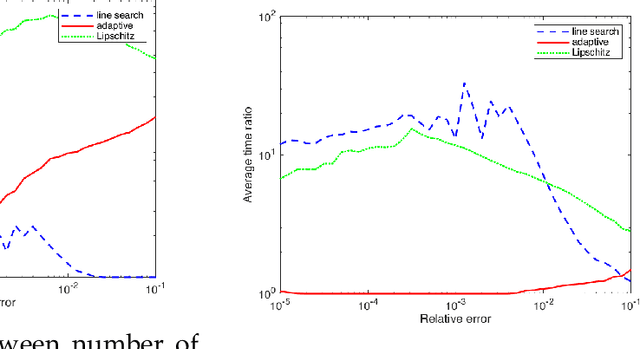
First-order methods for solving convex optimization problems have been at the forefront of mathematical optimization in the last 20 years. The rapid development of this important class of algorithms is motivated by the success stories reported in various applications, including most importantly machine learning, signal processing, imaging and control theory. First-order methods have the potential to provide low accuracy solutions at low computational complexity which makes them an attractive set of tools in large-scale optimization problems. In this survey we cover a number of key developments in gradient-based optimization methods. This includes non-Euclidean extensions of the classical proximal gradient method, and its accelerated versions. Additionally we survey recent developments within the class of projection-free methods, and proximal versions of primal-dual schemes. We give complete proofs for various key results, and highlight the unifying aspects of several optimization algorithms.

Self-concordant analysis of Frank-Wolfe algorithms

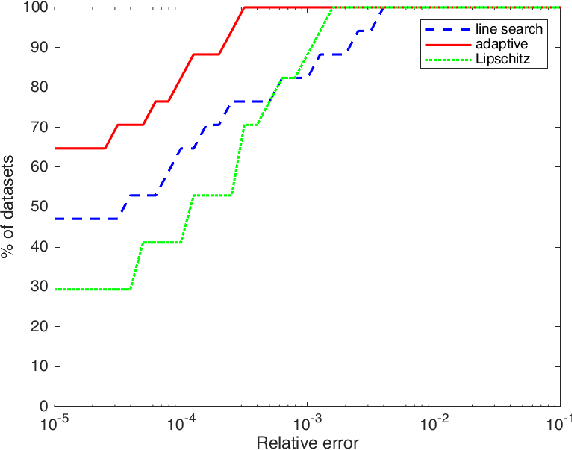
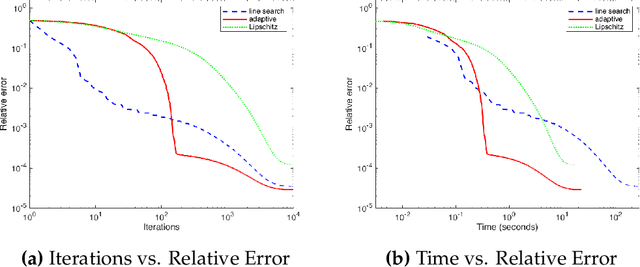
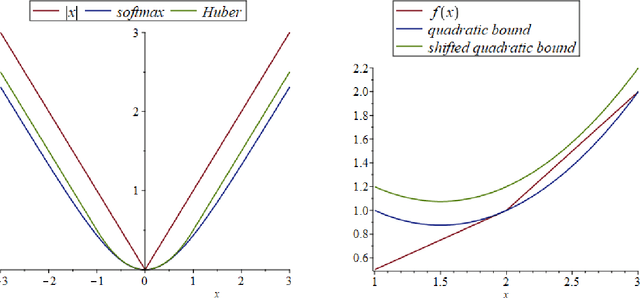
Projection-free optimization via different variants of the Frank-Wolfe (FW) method has become one of the cornerstones in optimization for machine learning since in many cases the linear minimization oracle is much cheaper to implement than projections and some sparsity needs to be preserved. In a number of applications, e.g. Poisson inverse problems or quantum state tomography, the loss is given by a self-concordant (SC) function having unbounded curvature, implying absence of theoretical guarantees for the existing FW methods. We use the theory of SC functions to provide a new adaptive step size for FW methods and prove global convergence rate O(1/k), k being the iteration counter. If the problem can be represented by a local linear minimization oracle, we are the first to propose a FW method with linear convergence rate without assuming neither strong convexity nor a Lipschitz continuous gradient.

Generalized Self-concordant Hessian-barrier algorithms

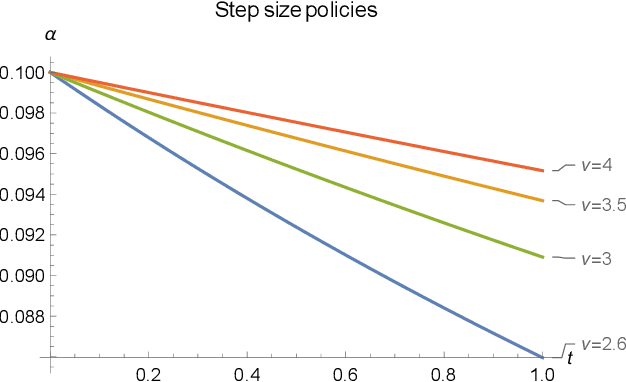
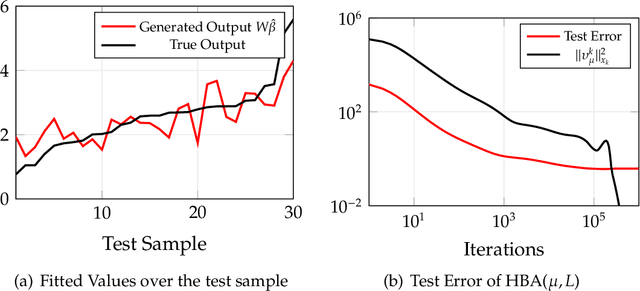
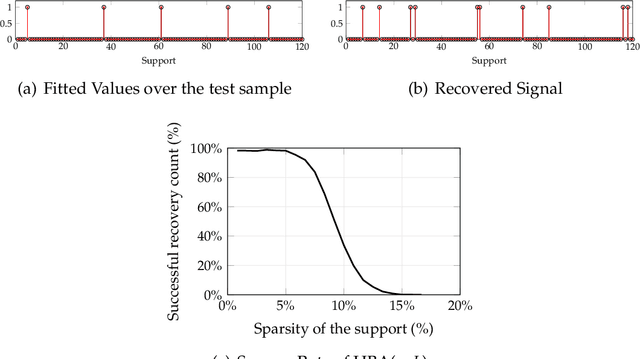
Many problems in statistical learning, imaging, and computer vision involve the optimization of a non-convex objective function with singularities at the boundary of the feasible set. For such challenging instances, we develop a new interior-point technique building on the Hessian-barrier algorithm recently introduced in Bomze, Mertikopoulos, Schachinger and Staudigl, [SIAM J. Opt. 2019 29(3), pp. 2100-2127], where the Riemannian metric is induced by a generalized self-concordant function. This class of functions is sufficiently general to include most of the commonly used barrier functions in the literature of interior point methods. We prove global convergence to an approximate stationary point of the method, and in cases where the feasible set admits an easily computable self-concordant barrier, we verify worst-case optimal iteration complexity of the method. Applications in non-convex statistical estimation and $L^{p}$-minimization are discussed to given the efficiency of the method.

Forward-backward-forward methods with variance reduction for stochastic variational inequalities

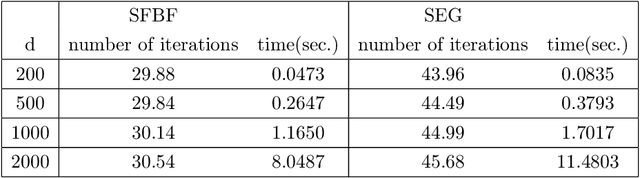
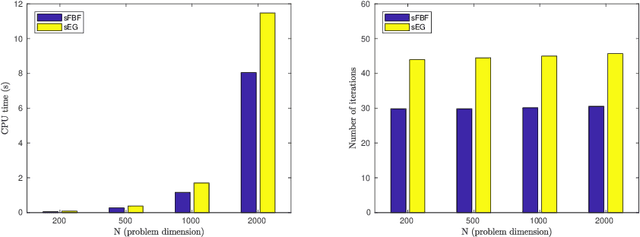
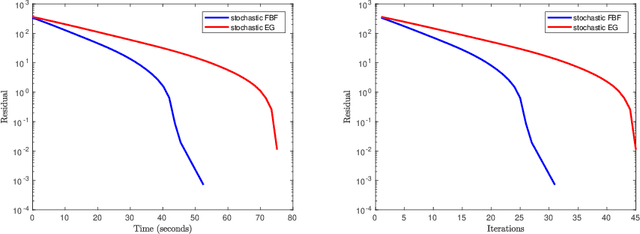
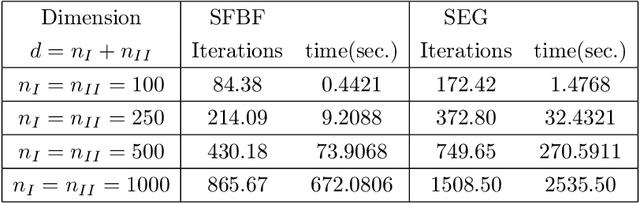
We develop a new stochastic algorithm with variance reduction for solving pseudo-monotone stochastic variational inequalities. Our method builds on Tseng's forward-backward-forward (FBF) algorithm, which is known in the deterministic literature to be a valuable alternative to Korpelevich's extragradient method when solving variational inequalities over a convex and closed set governed by pseudo-monotone, Lipschitz continuous operators. The main computational advantage of Tseng's algorithm is that it relies only on a single projection step and two independent queries of a stochastic oracle. Our algorithm incorporates a variance reduction mechanism and leads to almost sure (a.s.) convergence to an optimal solution. To the best of our knowledge, this is the first stochastic look-ahead algorithm achieving this by using only a single projection at each iteration..

Hessian barrier algorithms for linearly constrained optimization problems

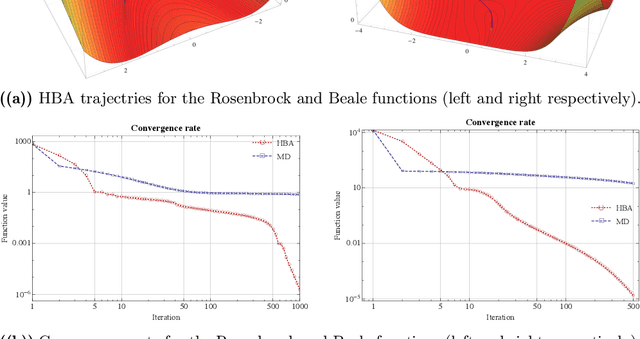
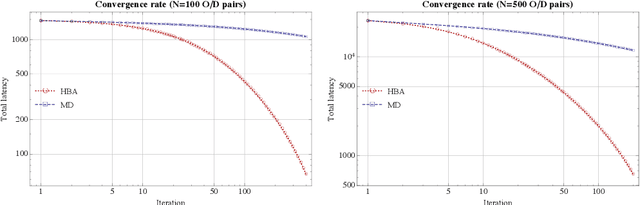
In this paper, we propose an interior-point method for linearly constrained optimization problems (possibly nonconvex). The method -- which we call the Hessian barrier algorithm (HBA) -- combines a forward Euler discretization of Hessian Riemannian gradient flows with an Armijo backtracking step-size policy. In this way, HBA can be seen as an explicit alternative to mirror descent (MD), and contains as special cases the affine scaling algorithm, regularized Newton processes, and several other iterative solution methods. Our main result is that, modulo a non-degeneracy condition, the algorithm converges to the problem's set of critical points; hence, in the convex case, the algorithm converges globally to the problem's minimum set. In the case of linearly constrained quadratic programs (not necessarily convex), we also show that the method's convergence rate is $\mathcal{O}(1/k^\rho)$ for some $\rho\in(0,1]$ that depends only on the choice of kernel function (i.e., not on the problem's primitives). These theoretical results are validated by numerical experiments in standard non-convex test functions and large-scale traffic assignment problems.

Learning in time-varying games

In this paper, we examine the long-term behavior of regret-minimizing agents in time-varying games with continuous action spaces. In its most basic form, (external) regret minimization guarantees that an agent's cumulative payoff is no worse in the long run than that of the agent's best fixed action in hindsight. Going beyond this worst-case guarantee, we consider a dynamic regret variant that compares the agent's accrued rewards to those of any sequence of play. Specializing to a wide class of no-regret strategies based on mirror descent, we derive explicit rates of regret minimization relying only on imperfect gradient obvservations. We then leverage these results to show that players are able to stay close to Nash equilibrium in time-varying monotone games - and even converge to Nash equilibrium if the sequence of stage games admits a limit.

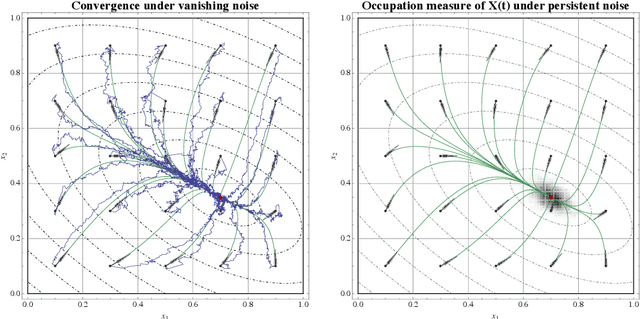
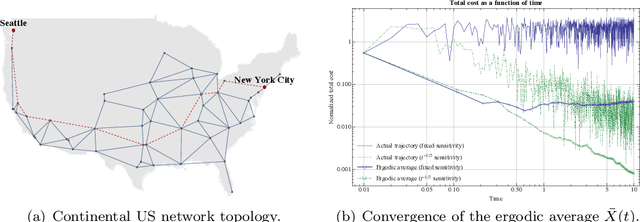
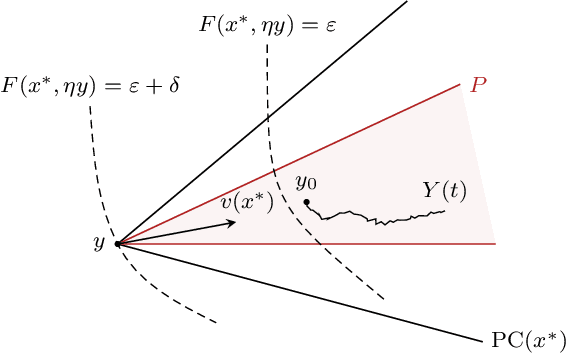
On the convergence of gradient-like flows with noisy gradient input

In view of solving convex optimization problems with noisy gradient input, we analyze the asymptotic behavior of gradient-like flows under stochastic disturbances. Specifically, we focus on the widely studied class of mirror descent schemes for convex programs with compact feasible regions, and we examine the dynamics' convergence and concentration properties in the presence of noise. In the vanishing noise limit, we show that the dynamics converge to the solution set of the underlying problem (a.s.). Otherwise, when the noise is persistent, we show that the dynamics are concentrated around interior solutions in the long run, and they converge to boundary solutions that are sufficiently "sharp". Finally, we show that a suitably rectified variant of the method converges irrespective of the magnitude of the noise (or the structure of the underlying convex program), and we derive an explicit estimate for its rate of convergence.