Efficient Swap Regret Minimization in Combinatorial Bandits

This paper addresses the problem of designing efficient no-swap regret algorithms for combinatorial bandits, where the number of actions $N$ is exponentially large in the dimensionality of the problem. In this setting, designing efficient no-swap regret translates to sublinear -- in horizon $T$ -- swap regret with polylogarithmic dependence on $N$. In contrast to the weaker notion of external regret minimization - a problem which is fairly well understood in the literature - achieving no-swap regret with a polylogarithmic dependence on $N$ has remained elusive in combinatorial bandits. Our paper resolves this challenge, by introducing a no-swap-regret learning algorithm with regret that scales polylogarithmically in $N$ and is tight for the class of combinatorial bandits. To ground our results, we also demonstrate how to implement the proposed algorithm efficiently -- that is, with a per-iteration complexity that also scales polylogarithmically in $N$ -- across a wide range of well-studied applications.

Robust equilibria in continuous games: From strategic to dynamic robustness

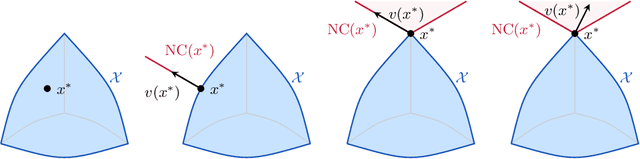
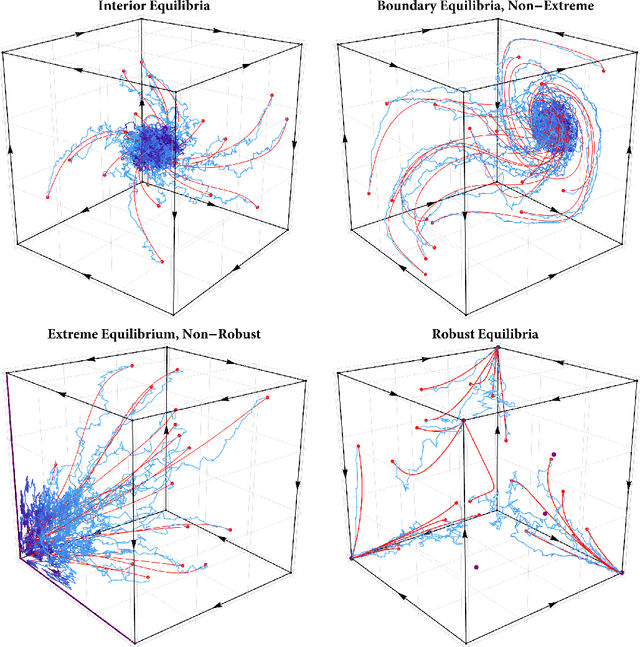
In this paper, we examine the robustness of Nash equilibria in continuous games, under both strategic and dynamic uncertainty. Starting with the former, we introduce the notion of a robust equilibrium as those equilibria that remain invariant to small -- but otherwise arbitrary -- perturbations to the game's payoff structure, and we provide a crisp geometric characterization thereof. Subsequently, we turn to the question of dynamic robustness, and we examine which equilibria may arise as stable limit points of the dynamics of "follow the regularized leader" (FTRL) in the presence of randomness and uncertainty. Despite their very distinct origins, we establish a structural correspondence between these two notions of robustness: strategic robustness implies dynamic robustness, and, conversely, the requirement of strategic robustness cannot be relaxed if dynamic robustness is to be maintained. Finally, we examine the rate of convergence to robust equilibria as a function of the underlying regularizer, and we show that entropically regularized learning converges at a geometric rate in games with affinely constrained action spaces.

Multi-agent learning under uncertainty: Recurrence vs. concentration

In this paper, we examine the convergence landscape of multi-agent learning under uncertainty. Specifically, we analyze two stochastic models of regularized learning in continuous games -- one in continuous and one in discrete time with the aim of characterizing the long-run behavior of the induced sequence of play. In stark contrast to deterministic, full-information models of learning (or models with a vanishing learning rate), we show that the resulting dynamics do not converge in general. In lieu of this, we ask instead which actions are played more often in the long run, and by how much. We show that, in strongly monotone games, the dynamics of regularized learning may wander away from equilibrium infinitely often, but they always return to its vicinity in finite time (which we estimate), and their long-run distribution is sharply concentrated around a neighborhood thereof. We quantify the degree of this concentration, and we show that these favorable properties may all break down if the underlying game is not strongly monotone -- underscoring in this way the limits of regularized learning in the presence of persistent randomness and uncertainty.

The impact of uncertainty on regularized learning in games

In this paper, we investigate how randomness and uncertainty influence learning in games. Specifically, we examine a perturbed variant of the dynamics of "follow-the-regularized-leader" (FTRL), where the players' payoff observations and strategy updates are continually impacted by random shocks. Our findings reveal that, in a fairly precise sense, "uncertainty favors extremes": in any game, regardless of the noise level, every player's trajectory of play reaches an arbitrarily small neighborhood of a pure strategy in finite time (which we estimate). Moreover, even if the player does not ultimately settle at this strategy, they return arbitrarily close to some (possibly different) pure strategy infinitely often. This prompts the question of which sets of pure strategies emerge as robust predictions of learning under uncertainty. We show that (a) the only possible limits of the FTRL dynamics under uncertainty are pure Nash equilibria; and (b) a span of pure strategies is stable and attracting if and only if it is closed under better replies. Finally, we turn to games where the deterministic dynamics are recurrent - such as zero-sum games with interior equilibria - and we show that randomness disrupts this behavior, causing the stochastic dynamics to drift toward the boundary on average.

The global convergence time of stochastic gradient descent in non-convex landscapes: Sharp estimates via large deviations

In this paper, we examine the time it takes for stochastic gradient descent (SGD) to reach the global minimum of a general, non-convex loss function. We approach this question through the lens of randomly perturbed dynamical systems and large deviations theory, and we provide a tight characterization of the global convergence time of SGD via matching upper and lower bounds. These bounds are dominated by the most "costly" set of obstacles that the algorithm may need to overcome to reach a global minimizer from a given initialization, coupling in this way the global geometry of the underlying loss landscape with the statistics of the noise entering the process. Finally, motivated by applications to the training of deep neural networks, we also provide a series of refinements and extensions of our analysis for loss functions with shallow local minima.

Accelerated regularized learning in finite N-person games

Motivated by the success of Nesterov's accelerated gradient algorithm for convex minimization problems, we examine whether it is possible to achieve similar performance gains in the context of online learning in games. To that end, we introduce a family of accelerated learning methods, which we call "follow the accelerated leader" (FTXL), and which incorporates the use of momentum within the general framework of regularized learning - and, in particular, the exponential/multiplicative weights algorithm and its variants. Drawing inspiration and techniques from the continuous-time analysis of Nesterov's algorithm, we show that FTXL converges locally to strict Nash equilibria at a superlinear rate, achieving in this way an exponential speed-up over vanilla regularized learning methods (which, by comparison, converge to strict equilibria at a geometric, linear rate). Importantly, FTXL maintains its superlinear convergence rate in a broad range of feedback structures, from deterministic, full information models to stochastic, realization-based ones, and even when run with bandit, payoff-based information, where players are only able to observe their individual realized payoffs.

No-regret learning in harmonic games: Extrapolation in the face of conflicting interests

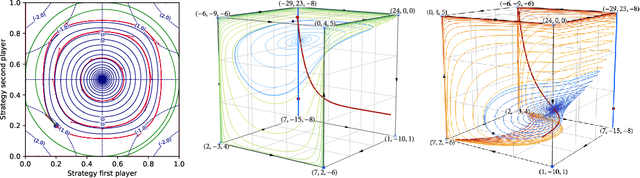
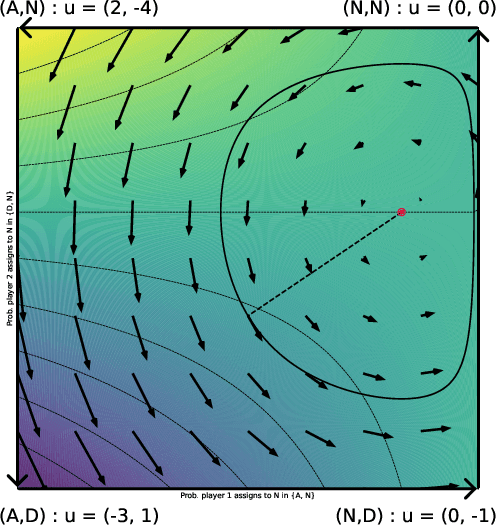
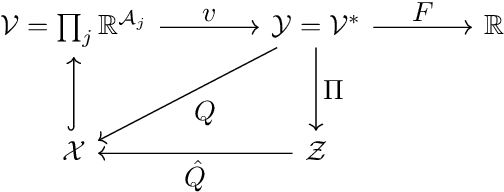
The long-run behavior of multi-agent learning - and, in particular, no-regret learning - is relatively well-understood in potential games, where players have aligned interests. By contrast, in harmonic games - the strategic counterpart of potential games, where players have conflicting interests - very little is known outside the narrow subclass of 2-player zero-sum games with a fully-mixed equilibrium. Our paper seeks to partially fill this gap by focusing on the full class of (generalized) harmonic games and examining the convergence properties of follow-the-regularized-leader (FTRL), the most widely studied class of no-regret learning schemes. As a first result, we show that the continuous-time dynamics of FTRL are Poincar\'e recurrent, that is, they return arbitrarily close to their starting point infinitely often, and hence fail to converge. In discrete time, the standard, "vanilla" implementation of FTRL may lead to even worse outcomes, eventually trapping the players in a perpetual cycle of best-responses. However, if FTRL is augmented with a suitable extrapolation step - which includes as special cases the optimistic and mirror-prox variants of FTRL - we show that learning converges to a Nash equilibrium from any initial condition, and all players are guaranteed at most O(1) regret. These results provide an in-depth understanding of no-regret learning in harmonic games, nesting prior work on 2-player zero-sum games, and showing at a high level that harmonic games are the canonical complement of potential games, not only from a strategic, but also from a dynamic viewpoint.

Nested replicator dynamics, nested logit choice, and similarity-based learning

We consider a model of learning and evolution in games whose action sets are endowed with a partition-based similarity structure intended to capture exogenous similarities between strategies. In this model, revising agents have a higher probability of comparing their current strategy with other strategies that they deem similar, and they switch to the observed strategy with probability proportional to its payoff excess. Because of this implicit bias toward similar strategies, the resulting dynamics - which we call the nested replicator dynamics - do not satisfy any of the standard monotonicity postulates for imitative game dynamics; nonetheless, we show that they retain the main long-run rationality properties of the replicator dynamics, albeit at quantitatively different rates. We also show that the induced dynamics can be viewed as a stimulus-response model in the spirit of Erev & Roth (1998), with choice probabilities given by the nested logit choice rule of Ben-Akiva (1973) and McFadden (1978). This result generalizes an existing relation between the replicator dynamics and the exponential weights algorithm in online learning, and provides an additional layer of interpretation to our analysis and results.

What is the long-run distribution of stochastic gradient descent? A large deviations analysis

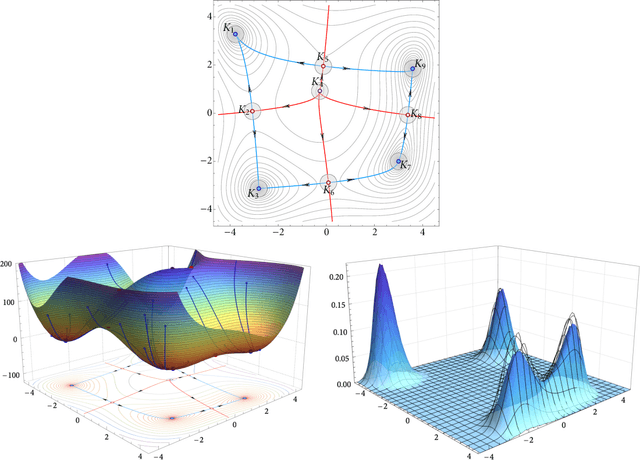
In this paper, we examine the long-run distribution of stochastic gradient descent (SGD) in general, non-convex problems. Specifically, we seek to understand which regions of the problem's state space are more likely to be visited by SGD, and by how much. Using an approach based on the theory of large deviations and randomly perturbed dynamical systems, we show that the long-run distribution of SGD resembles the Boltzmann-Gibbs distribution of equilibrium thermodynamics with temperature equal to the method's step-size and energy levels determined by the problem's objective and the statistics of the noise. In particular, we show that, in the long run, (a) the problem's critical region is visited exponentially more often than any non-critical region; (b) the iterates of SGD are exponentially concentrated around the problem's minimum energy state (which does not always coincide with the global minimum of the objective); (c) all other connected components of critical points are visited with frequency that is exponentially proportional to their energy level; and, finally (d) any component of local maximizers or saddle points is "dominated" by a component of local minimizers which is visited exponentially more often.

Tamed Langevin sampling under weaker conditions

Motivated by applications to deep learning which often fail standard Lipschitz smoothness requirements, we examine the problem of sampling from distributions that are not log-concave and are only weakly dissipative, with log-gradients allowed to grow superlinearly at infinity. In terms of structure, we only assume that the target distribution satisfies either a log-Sobolev or a Poincar\'e inequality and a local Lipschitz smoothness assumption with modulus growing possibly polynomially at infinity. This set of assumptions greatly exceeds the operational limits of the "vanilla" unadjusted Langevin algorithm (ULA), making sampling from such distributions a highly involved affair. To account for this, we introduce a taming scheme which is tailored to the growth and decay properties of the target distribution, and we provide explicit non-asymptotic guarantees for the proposed sampler in terms of the Kullback-Leibler (KL) divergence, total variation, and Wasserstein distance to the target distribution.