Kyriakos Lotidis
Multi-agent learning under uncertainty: Recurrence vs. concentration
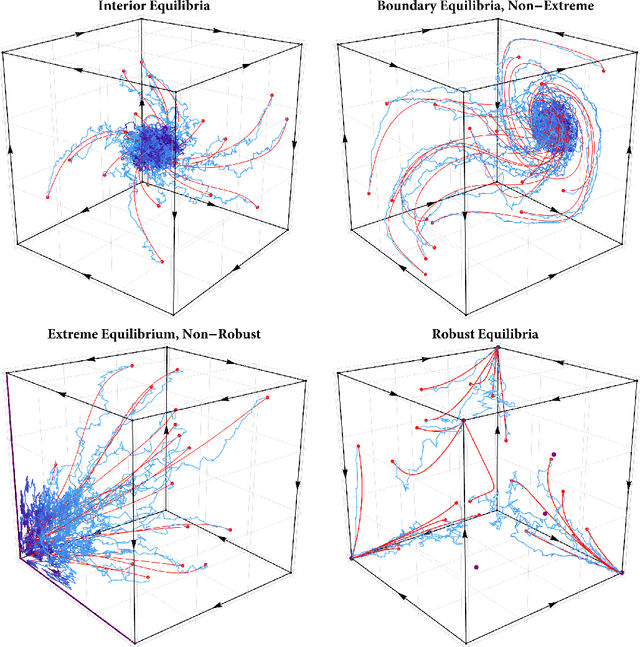
Dec 09, 2025Abstract:In this paper, we examine the convergence landscape of multi-agent learning under uncertainty. Specifically, we analyze two stochastic models of regularized learning in continuous games -- one in continuous and one in discrete time with the aim of characterizing the long-run behavior of the induced sequence of play. In stark contrast to deterministic, full-information models of learning (or models with a vanishing learning rate), we show that the resulting dynamics do not converge in general. In lieu of this, we ask instead which actions are played more often in the long run, and by how much. We show that, in strongly monotone games, the dynamics of regularized learning may wander away from equilibrium infinitely often, but they always return to its vicinity in finite time (which we estimate), and their long-run distribution is sharply concentrated around a neighborhood thereof. We quantify the degree of this concentration, and we show that these favorable properties may all break down if the underlying game is not strongly monotone -- underscoring in this way the limits of regularized learning in the presence of persistent randomness and uncertainty.
Robust equilibria in continuous games: From strategic to dynamic robustness
Dec 09, 2025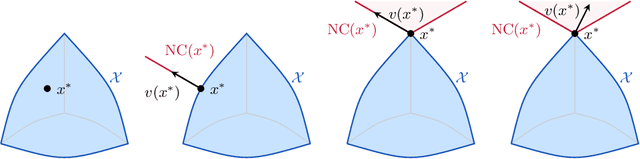
Abstract:In this paper, we examine the robustness of Nash equilibria in continuous games, under both strategic and dynamic uncertainty. Starting with the former, we introduce the notion of a robust equilibrium as those equilibria that remain invariant to small -- but otherwise arbitrary -- perturbations to the game's payoff structure, and we provide a crisp geometric characterization thereof. Subsequently, we turn to the question of dynamic robustness, and we examine which equilibria may arise as stable limit points of the dynamics of "follow the regularized leader" (FTRL) in the presence of randomness and uncertainty. Despite their very distinct origins, we establish a structural correspondence between these two notions of robustness: strategic robustness implies dynamic robustness, and, conversely, the requirement of strategic robustness cannot be relaxed if dynamic robustness is to be maintained. Finally, we examine the rate of convergence to robust equilibria as a function of the underlying regularizer, and we show that entropically regularized learning converges at a geometric rate in games with affinely constrained action spaces.
Accelerated regularized learning in finite N-person games
Dec 29, 2024Abstract:Motivated by the success of Nesterov's accelerated gradient algorithm for convex minimization problems, we examine whether it is possible to achieve similar performance gains in the context of online learning in games. To that end, we introduce a family of accelerated learning methods, which we call "follow the accelerated leader" (FTXL), and which incorporates the use of momentum within the general framework of regularized learning - and, in particular, the exponential/multiplicative weights algorithm and its variants. Drawing inspiration and techniques from the continuous-time analysis of Nesterov's algorithm, we show that FTXL converges locally to strict Nash equilibria at a superlinear rate, achieving in this way an exponential speed-up over vanilla regularized learning methods (which, by comparison, converge to strict equilibria at a geometric, linear rate). Importantly, FTXL maintains its superlinear convergence rate in a broad range of feedback structures, from deterministic, full information models to stochastic, realization-based ones, and even when run with bandit, payoff-based information, where players are only able to observe their individual realized payoffs.
Payoff-based learning with matrix multiplicative weights in quantum games
Nov 04, 2023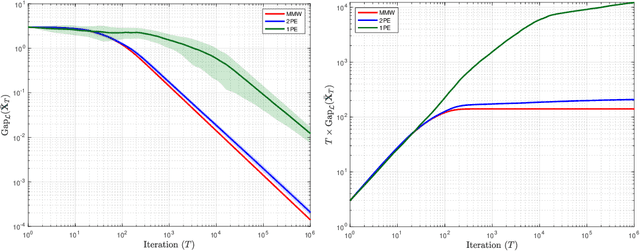
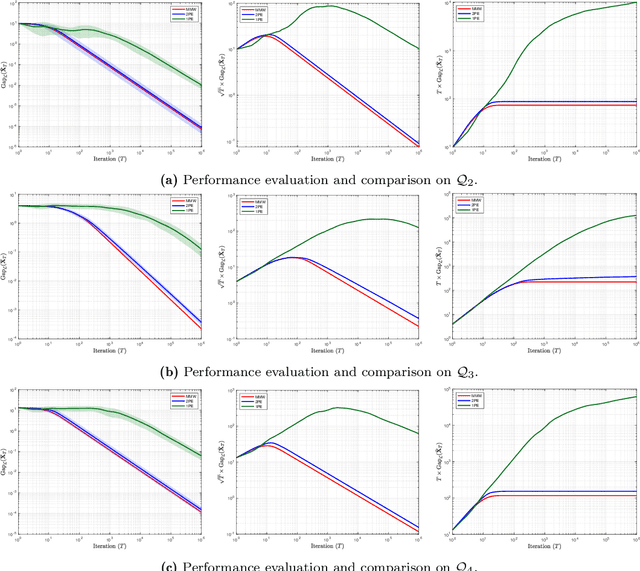
Abstract:In this paper, we study the problem of learning in quantum games - and other classes of semidefinite games - with scalar, payoff-based feedback. For concreteness, we focus on the widely used matrix multiplicative weights (MMW) algorithm and, instead of requiring players to have full knowledge of the game (and/or each other's chosen states), we introduce a suite of minimal-information matrix multiplicative weights (3MW) methods tailored to different information frameworks. The main difficulty to attaining convergence in this setting is that, in contrast to classical finite games, quantum games have an infinite continuum of pure states (the quantum equivalent of pure strategies), so standard importance-weighting techniques for estimating payoff vectors cannot be employed. Instead, we borrow ideas from bandit convex optimization and we design a zeroth-order gradient sampler adapted to the semidefinite geometry of the problem at hand. As a first result, we show that the 3MW method with deterministic payoff feedback retains the $\mathcal{O}(1/\sqrt{T})$ convergence rate of the vanilla, full information MMW algorithm in quantum min-max games, even though the players only observe a single scalar. Subsequently, we relax the algorithm's information requirements even further and we provide a 3MW method that only requires players to observe a random realization of their payoff observable, and converges to equilibrium at an $\mathcal{O}(T^{-1/4})$ rate. Finally, going beyond zero-sum games, we show that a regularized variant of the proposed 3MW method guarantees local convergence with high probability to all equilibria that satisfy a certain first-order stability condition.
Learning in quantum games
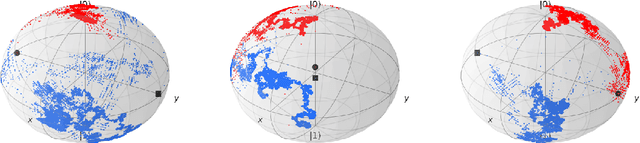
Feb 05, 2023Abstract:In this paper, we introduce a class of learning dynamics for general quantum games, that we call "follow the quantum regularized leader" (FTQL), in reference to the classical "follow the regularized leader" (FTRL) template for learning in finite games. We show that the induced quantum state dynamics decompose into (i) a classical, commutative component which governs the dynamics of the system's eigenvalues in a way analogous to the evolution of mixed strategies under FTRL; and (ii) a non-commutative component for the system's eigenvectors which has no classical counterpart. Despite the complications that this non-classical component entails, we find that the FTQL dynamics incur no more than constant regret in all quantum games. Moreover, adjusting classical notions of stability to account for the nonlinear geometry of the state space of quantum games, we show that only pure quantum equilibria can be stable and attracting under FTQL while, as a partial converse, pure equilibria that satisfy a certain "variational stability" condition are always attracting. Finally, we show that the FTQL dynamics are Poincar\'e recurrent in quantum min-max games, extending in this way a very recent result for the quantum replicator dynamics.
On the convergence of policy gradient methods to Nash equilibria in general stochastic games
Oct 17, 2022Abstract:Learning in stochastic games is a notoriously difficult problem because, in addition to each other's strategic decisions, the players must also contend with the fact that the game itself evolves over time, possibly in a very complicated manner. Because of this, the convergence properties of popular learning algorithms - like policy gradient and its variants - are poorly understood, except in specific classes of games (such as potential or two-player, zero-sum games). In view of this, we examine the long-run behavior of policy gradient methods with respect to Nash equilibrium policies that are second-order stationary (SOS) in a sense similar to the type of sufficiency conditions used in optimization. Our first result is that SOS policies are locally attracting with high probability, and we show that policy gradient trajectories with gradient estimates provided by the REINFORCE algorithm achieve an $\mathcal{O}(1/\sqrt{n})$ distance-squared convergence rate if the method's step-size is chosen appropriately. Subsequently, specializing to the class of deterministic Nash policies, we show that this rate can be improved dramatically and, in fact, policy gradient methods converge within a finite number of iterations in that case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge