Nested replicator dynamics, nested logit choice, and similarity-based learning

We consider a model of learning and evolution in games whose action sets are endowed with a partition-based similarity structure intended to capture exogenous similarities between strategies. In this model, revising agents have a higher probability of comparing their current strategy with other strategies that they deem similar, and they switch to the observed strategy with probability proportional to its payoff excess. Because of this implicit bias toward similar strategies, the resulting dynamics - which we call the nested replicator dynamics - do not satisfy any of the standard monotonicity postulates for imitative game dynamics; nonetheless, we show that they retain the main long-run rationality properties of the replicator dynamics, albeit at quantitatively different rates. We also show that the induced dynamics can be viewed as a stimulus-response model in the spirit of Erev & Roth (1998), with choice probabilities given by the nested logit choice rule of Ben-Akiva (1973) and McFadden (1978). This result generalizes an existing relation between the replicator dynamics and the exponential weights algorithm in online learning, and provides an additional layer of interpretation to our analysis and results.

Learning in games via reinforcement and regularization

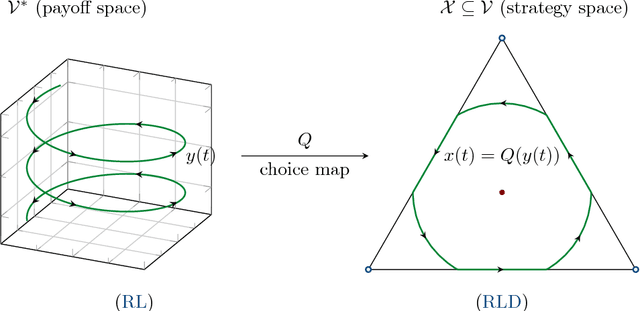
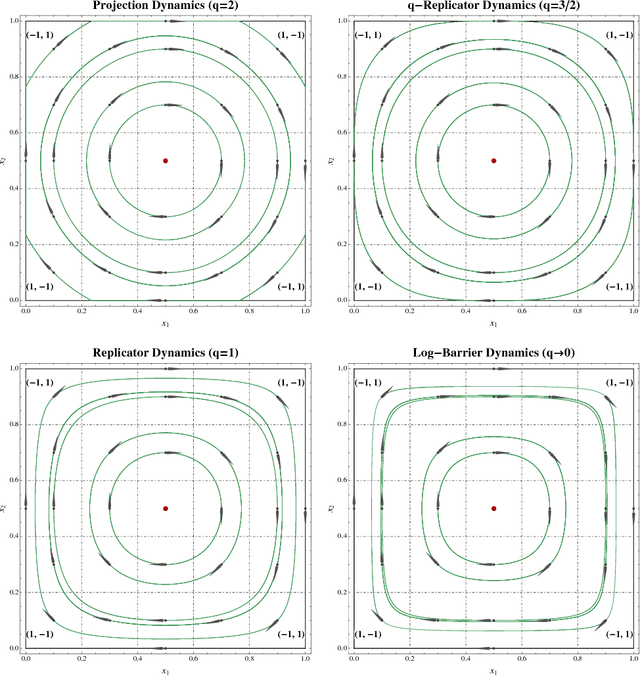
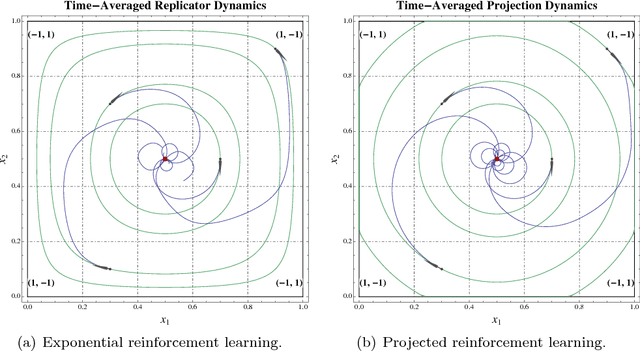
We investigate a class of reinforcement learning dynamics where players adjust their strategies based on their actions' cumulative payoffs over time - specifically, by playing mixed strategies that maximize their expected cumulative payoff minus a regularization term. A widely studied example is exponential reinforcement learning, a process induced by an entropic regularization term which leads mixed strategies to evolve according to the replicator dynamics. However, in contrast to the class of regularization functions used to define smooth best responses in models of stochastic fictitious play, the functions used in this paper need not be infinitely steep at the boundary of the simplex; in fact, dropping this requirement gives rise to an important dichotomy between steep and nonsteep cases. In this general framework, we extend several properties of exponential learning, including the elimination of dominated strategies, the asymptotic stability of strict Nash equilibria, and the convergence of time-averaged trajectories in zero-sum games with an interior Nash equilibrium.