kTULA: A Langevin sampling algorithm with improved KL bounds under super-linear log-gradients

Motivated by applications in deep learning, where the global Lipschitz continuity condition is often not satisfied, we examine the problem of sampling from distributions with super-linearly growing log-gradients. We propose a novel tamed Langevin dynamics-based algorithm, called kTULA, to solve the aforementioned sampling problem, and provide a theoretical guarantee for its performance. More precisely, we establish a non-asymptotic convergence bound in Kullback-Leibler (KL) divergence with the best-known rate of convergence equal to $2-\overline{\epsilon}$, $\overline{\epsilon}>0$, which significantly improves relevant results in existing literature. This enables us to obtain an improved non-asymptotic error bound in Wasserstein-2 distance, which can be used to further derive a non-asymptotic guarantee for kTULA to solve the associated optimization problems. To illustrate the applicability of kTULA, we apply the proposed algorithm to the problem of sampling from a high-dimensional double-well potential distribution and to an optimization problem involving a neural network. We show that our main results can be used to provide theoretical guarantees for the performance of kTULA.

The Performance Of The Unadjusted Langevin Algorithm Without Smoothness Assumptions

In this article, we study the problem of sampling from distributions whose densities are not necessarily smooth nor log-concave. We propose a simple Langevin-based algorithm that does not rely on popular but computationally challenging techniques, such as the Moreau Yosida envelope or Gaussian smoothing. We derive non-asymptotic guarantees for the convergence of the algorithm to the target distribution in Wasserstein distances. Non asymptotic bounds are also provided for the performance of the algorithm as an optimizer, specifically for the solution of associated excess risk optimization problems.

Tamed Langevin sampling under weaker conditions

Motivated by applications to deep learning which often fail standard Lipschitz smoothness requirements, we examine the problem of sampling from distributions that are not log-concave and are only weakly dissipative, with log-gradients allowed to grow superlinearly at infinity. In terms of structure, we only assume that the target distribution satisfies either a log-Sobolev or a Poincar\'e inequality and a local Lipschitz smoothness assumption with modulus growing possibly polynomially at infinity. This set of assumptions greatly exceeds the operational limits of the "vanilla" unadjusted Langevin algorithm (ULA), making sampling from such distributions a highly involved affair. To account for this, we introduce a taming scheme which is tailored to the growth and decay properties of the target distribution, and we provide explicit non-asymptotic guarantees for the proposed sampler in terms of the Kullback-Leibler (KL) divergence, total variation, and Wasserstein distance to the target distribution.

Taming under isoperimetry

In this article we propose a novel taming Langevin-based scheme called $\mathbf{sTULA}$ to sample from distributions with superlinearly growing log-gradient which also satisfy a Log-Sobolev inequality. We derive non-asymptotic convergence bounds in $KL$ and consequently total variation and Wasserstein-$2$ distance from the target measure. Non-asymptotic convergence guarantees are provided for the performance of the new algorithm as an optimizer. Finally, some theoretical results on isoperimertic inequalities for distributions with superlinearly growing gradients are provided. Key findings are a Log-Sobolev inequality with constant independent of the dimension, in the presence of a higher order regularization and a Poincare inequality with constant independent of temperature and dimension under a novel non-convex theoretical framework.

Kinetic Langevin MCMC Sampling Without Gradient Lipschitz Continuity -- the Strongly Convex Case

In this article we consider sampling from log concave distributions in Hamiltonian setting, without assuming that the objective gradient is globally Lipschitz. We propose two algorithms based on monotone polygonal (tamed) Euler schemes, to sample from a target measure, and provide non-asymptotic 2-Wasserstein distance bounds between the law of the process of each algorithm and the target measure. Finally, we apply these results to bound the excess risk optimization error of the associated optimization problem.

Taming neural networks with TUSLA: Non-convex learning via adaptive stochastic gradient Langevin algorithms

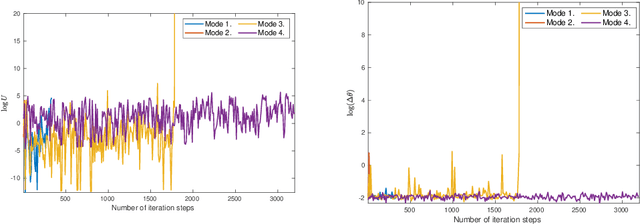
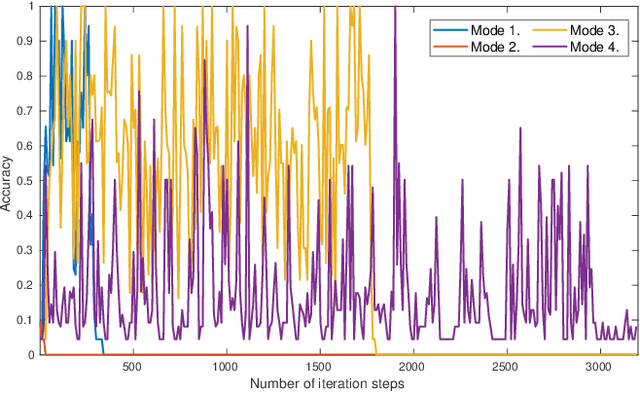
Artificial neural networks (ANNs) are typically highly nonlinear systems which are finely tuned via the optimization of their associated, non-convex loss functions. Typically, the gradient of any such loss function fails to be dissipative making the use of widely-accepted (stochastic) gradient descent methods problematic. We offer a new learning algorithm based on an appropriately constructed variant of the popular stochastic gradient Langevin dynamics (SGLD), which is called tamed unadjusted stochastic Langevin algorithm (TUSLA). We also provide a nonasymptotic analysis of the new algorithm's convergence properties in the context of non-convex learning problems with the use of ANNs. Thus, we provide finite-time guarantees for TUSLA to find approximate minimizers of both empirical and population risks. The roots of the TUSLA algorithm are based on the taming technology for diffusion processes with superlinear coefficients as developed in Sabanis (2013, 2016) and for MCMC algorithms in Brosse et al. (2019). Numerical experiments are presented which confirm the theoretical findings and illustrate the need for the use of the new algorithm in comparison to vanilla SGLD within the framework of ANNs.