Transition of $α$-mixing in Random Iterations with Applications in Queuing Theory

Nonlinear time series models incorporating exogenous regressors provide the foundation for numerous significant models across econometrics, queuing theory, machine learning, and various other disciplines. Despite their importance, the framework for the statistical analysis of such models is still incomplete. In contrast, multiple versions of the law of large numbers and the (functional) central limit theorem have been established for weakly dependent variables. We prove the transition of mixing properties of the exogenous regressor to the response through a coupling argument, leveraging these established results. Furthermore, we study Markov chains in random environments under a suitable form of drift and minorization condition when the environment process is non-stationary, merely having favorable mixing properties. Following a novel statistical estimation theory approach and using the Cram\'er-Rao lower bound, we also establish the functional central limit theorem. Additionally, we apply our framework to single-server queuing models. Overall, these results open the door to the statistical analysis of a large class of random iterative models.

On the strong stability of ergodic iterations

We revisit processes generated by iterated random functions driven by a stationary and ergodic sequence. Such a process is called strongly stable if a random initialization exists, for which the process is stationary and ergodic, and for any other initialization, the difference of the two processes converges to zero almost surely. Under some mild conditions on the corresponding recursive map, without any condition on the driving sequence, we show the strong stability of iterations. Several applications are surveyed such as stochastic approximation and queuing. Furthermore, new results are deduced for Langevin-type iterations with dependent noise and for multitype branching processes.

Functional Central Limit Theorem and Strong Law of Large Numbers for Stochastic Gradient Langevin Dynamics

We study the mixing properties of an important optimization algorithm of machine learning: the stochastic gradient Langevin dynamics (SGLD) with a fixed step size. The data stream is not assumed to be independent hence the SGLD is not a Markov chain, merely a \emph{Markov chain in a random environment}, which complicates the mathematical treatment considerably. We derive a strong law of large numbers and a functional central limit theorem for SGLD.

Taming neural networks with TUSLA: Non-convex learning via adaptive stochastic gradient Langevin algorithms

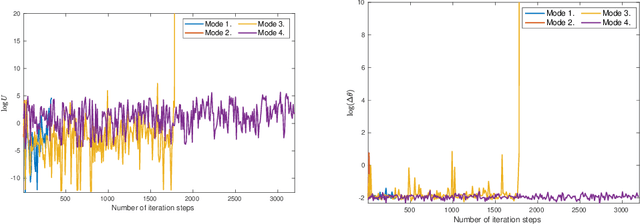
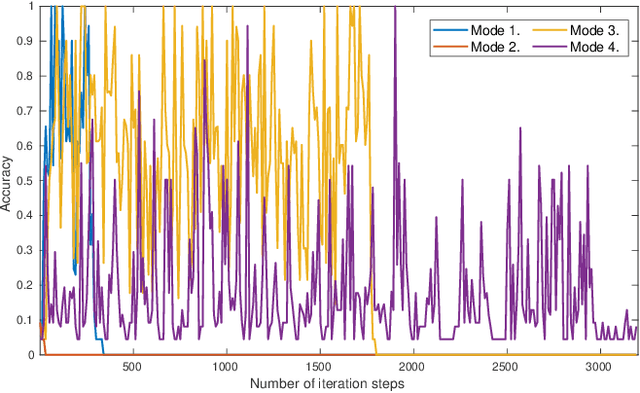
Artificial neural networks (ANNs) are typically highly nonlinear systems which are finely tuned via the optimization of their associated, non-convex loss functions. Typically, the gradient of any such loss function fails to be dissipative making the use of widely-accepted (stochastic) gradient descent methods problematic. We offer a new learning algorithm based on an appropriately constructed variant of the popular stochastic gradient Langevin dynamics (SGLD), which is called tamed unadjusted stochastic Langevin algorithm (TUSLA). We also provide a nonasymptotic analysis of the new algorithm's convergence properties in the context of non-convex learning problems with the use of ANNs. Thus, we provide finite-time guarantees for TUSLA to find approximate minimizers of both empirical and population risks. The roots of the TUSLA algorithm are based on the taming technology for diffusion processes with superlinear coefficients as developed in Sabanis (2013, 2016) and for MCMC algorithms in Brosse et al. (2019). Numerical experiments are presented which confirm the theoretical findings and illustrate the need for the use of the new algorithm in comparison to vanilla SGLD within the framework of ANNs.

Markov chains in random environment with applications in queueing theory and machine learning

We prove the existence of limiting distributions for a large class of Markov chains on a general state space in a random environment. We assume suitable versions of the standard drift and minorization conditions. In particular, the system dynamics should be contractive on the average with respect to the Lyapunov function and large enough small sets should exist with large enough minorization constants. We also establish that a law of large numbers holds for bounded functionals of the process. Applications to queuing systems and to machine learning algorithms are presented.