What is the long-run distribution of stochastic gradient descent? A large deviations analysis
Paper and Code
Jun 13, 2024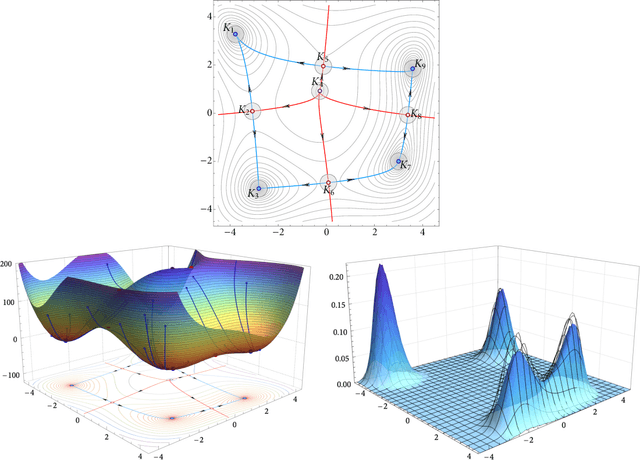
In this paper, we examine the long-run distribution of stochastic gradient descent (SGD) in general, non-convex problems. Specifically, we seek to understand which regions of the problem's state space are more likely to be visited by SGD, and by how much. Using an approach based on the theory of large deviations and randomly perturbed dynamical systems, we show that the long-run distribution of SGD resembles the Boltzmann-Gibbs distribution of equilibrium thermodynamics with temperature equal to the method's step-size and energy levels determined by the problem's objective and the statistics of the noise. In particular, we show that, in the long run, (a) the problem's critical region is visited exponentially more often than any non-critical region; (b) the iterates of SGD are exponentially concentrated around the problem's minimum energy state (which does not always coincide with the global minimum of the objective); (c) all other connected components of critical points are visited with frequency that is exponentially proportional to their energy level; and, finally (d) any component of local maximizers or saddle points is "dominated" by a component of local minimizers which is visited exponentially more often.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge