The impact of uncertainty on regularized learning in games

In this paper, we investigate how randomness and uncertainty influence learning in games. Specifically, we examine a perturbed variant of the dynamics of "follow-the-regularized-leader" (FTRL), where the players' payoff observations and strategy updates are continually impacted by random shocks. Our findings reveal that, in a fairly precise sense, "uncertainty favors extremes": in any game, regardless of the noise level, every player's trajectory of play reaches an arbitrarily small neighborhood of a pure strategy in finite time (which we estimate). Moreover, even if the player does not ultimately settle at this strategy, they return arbitrarily close to some (possibly different) pure strategy infinitely often. This prompts the question of which sets of pure strategies emerge as robust predictions of learning under uncertainty. We show that (a) the only possible limits of the FTRL dynamics under uncertainty are pure Nash equilibria; and (b) a span of pure strategies is stable and attracting if and only if it is closed under better replies. Finally, we turn to games where the deterministic dynamics are recurrent - such as zero-sum games with interior equilibria - and we show that randomness disrupts this behavior, causing the stochastic dynamics to drift toward the boundary on average.

No-regret learning in harmonic games: Extrapolation in the face of conflicting interests

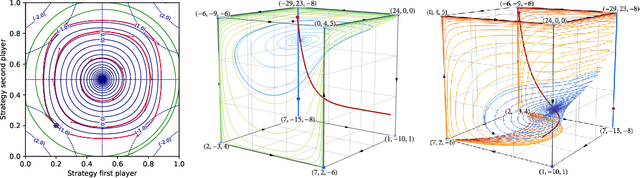
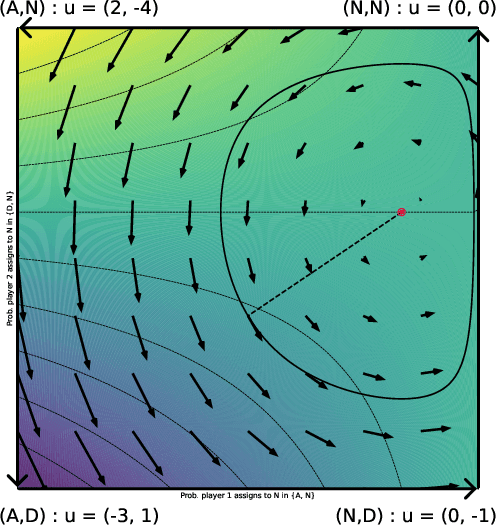
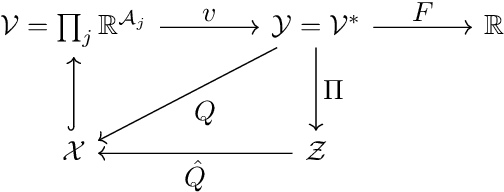
The long-run behavior of multi-agent learning - and, in particular, no-regret learning - is relatively well-understood in potential games, where players have aligned interests. By contrast, in harmonic games - the strategic counterpart of potential games, where players have conflicting interests - very little is known outside the narrow subclass of 2-player zero-sum games with a fully-mixed equilibrium. Our paper seeks to partially fill this gap by focusing on the full class of (generalized) harmonic games and examining the convergence properties of follow-the-regularized-leader (FTRL), the most widely studied class of no-regret learning schemes. As a first result, we show that the continuous-time dynamics of FTRL are Poincar\'e recurrent, that is, they return arbitrarily close to their starting point infinitely often, and hence fail to converge. In discrete time, the standard, "vanilla" implementation of FTRL may lead to even worse outcomes, eventually trapping the players in a perpetual cycle of best-responses. However, if FTRL is augmented with a suitable extrapolation step - which includes as special cases the optimistic and mirror-prox variants of FTRL - we show that learning converges to a Nash equilibrium from any initial condition, and all players are guaranteed at most O(1) regret. These results provide an in-depth understanding of no-regret learning in harmonic games, nesting prior work on 2-player zero-sum games, and showing at a high level that harmonic games are the canonical complement of potential games, not only from a strategic, but also from a dynamic viewpoint.

A geometric decomposition of finite games: Convergence vs. recurrence under no-regret learning

In view of the complexity of the dynamics of no-regret learning in games, we seek to decompose a finite game into simpler components where the day-to-day behavior of the dynamics is well understood. A natural starting point for this is Helmholtz's theorem, which resolves a vector field into a potential and an incompressible component. However, the geometry of no-regret dynamics - and, in particular, the dynamics of exponential / multiplicative weights (EW) schemes - is not compatible with the Euclidean underpinnings of Helmholtz's theorem, leading us to consider a Riemannian framework based on the Shahshahani metric. Using this geometric construction, we introduce the class of incompressible games, and we prove the following results: First, in addition to being volume-preserving, the continuous-time EW dynamics in incompressible games admit a constant of motion and are Poincar\'e recurrent - i.e., almost every trajectory of play comes arbitrarily close to its starting point infinitely often. Second, we establish a deep connection with a well-known decomposition of games into a potential and harmonic component (where the players' objectives are aligned and anti-aligned respectively): a game is incompressible if and only if it is harmonic, implying in turn that the EW dynamics lead to Poincar\'e recurrence in harmonic games.