No-regret learning in harmonic games: Extrapolation in the face of conflicting interests

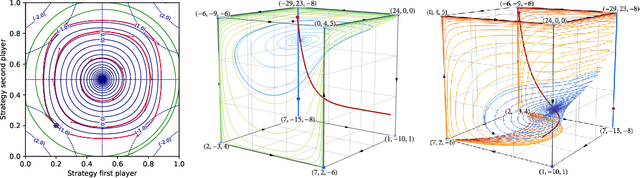
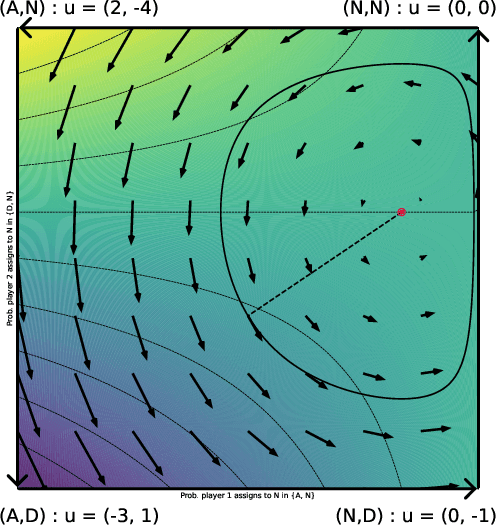
The long-run behavior of multi-agent learning - and, in particular, no-regret learning - is relatively well-understood in potential games, where players have aligned interests. By contrast, in harmonic games - the strategic counterpart of potential games, where players have conflicting interests - very little is known outside the narrow subclass of 2-player zero-sum games with a fully-mixed equilibrium. Our paper seeks to partially fill this gap by focusing on the full class of (generalized) harmonic games and examining the convergence properties of follow-the-regularized-leader (FTRL), the most widely studied class of no-regret learning schemes. As a first result, we show that the continuous-time dynamics of FTRL are Poincar\'e recurrent, that is, they return arbitrarily close to their starting point infinitely often, and hence fail to converge. In discrete time, the standard, "vanilla" implementation of FTRL may lead to even worse outcomes, eventually trapping the players in a perpetual cycle of best-responses. However, if FTRL is augmented with a suitable extrapolation step - which includes as special cases the optimistic and mirror-prox variants of FTRL - we show that learning converges to a Nash equilibrium from any initial condition, and all players are guaranteed at most O(1) regret. These results provide an in-depth understanding of no-regret learning in harmonic games, nesting prior work on 2-player zero-sum games, and showing at a high level that harmonic games are the canonical complement of potential games, not only from a strategic, but also from a dynamic viewpoint.

Selection in the Presence of Implicit Bias: The Advantage of Intersectional Constraints

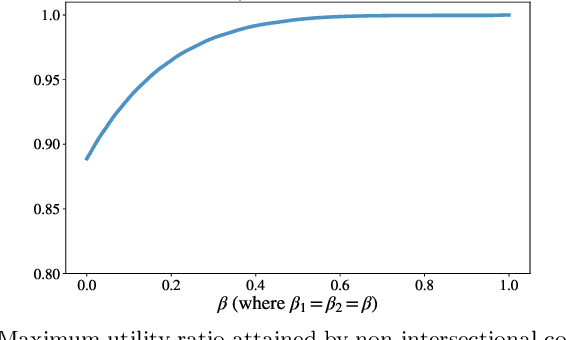
In selection processes such as hiring, promotion, and college admissions, implicit bias toward socially-salient attributes such as race, gender, or sexual orientation of candidates is known to produce persistent inequality and reduce aggregate utility for the decision maker. Interventions such as the Rooney Rule and its generalizations, which require the decision maker to select at least a specified number of individuals from each affected group, have been proposed to mitigate the adverse effects of implicit bias in selection. Recent works have established that such lower-bound constraints can be very effective in improving aggregate utility in the case when each individual belongs to at most one affected group. However, in several settings, individuals may belong to multiple affected groups and, consequently, face more extreme implicit bias due to this intersectionality. We consider independently drawn utilities and show that, in the intersectional case, the aforementioned non-intersectional constraints can only recover part of the total utility achievable in the absence of implicit bias. On the other hand, we show that if one includes appropriate lower-bound constraints on the intersections, almost all the utility achievable in the absence of implicit bias can be recovered. Thus, intersectional constraints can offer a significant advantage over a reductionist dimension-by-dimension non-intersectional approach to reducing inequality.