Werner Schachinger
Hessian barrier algorithms for linearly constrained optimization problems
Sep 25, 2018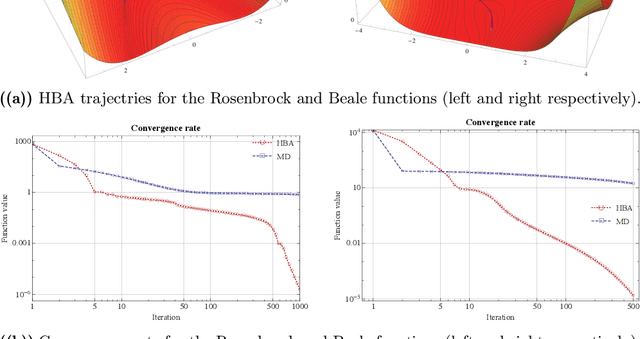
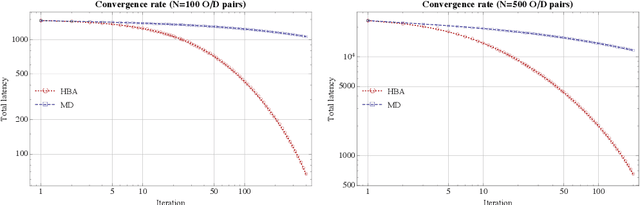
Abstract:In this paper, we propose an interior-point method for linearly constrained optimization problems (possibly nonconvex). The method -- which we call the Hessian barrier algorithm (HBA) -- combines a forward Euler discretization of Hessian Riemannian gradient flows with an Armijo backtracking step-size policy. In this way, HBA can be seen as an explicit alternative to mirror descent (MD), and contains as special cases the affine scaling algorithm, regularized Newton processes, and several other iterative solution methods. Our main result is that, modulo a non-degeneracy condition, the algorithm converges to the problem's set of critical points; hence, in the convex case, the algorithm converges globally to the problem's minimum set. In the case of linearly constrained quadratic programs (not necessarily convex), we also show that the method's convergence rate is $\mathcal{O}(1/k^\rho)$ for some $\rho\in(0,1]$ that depends only on the choice of kernel function (i.e., not on the problem's primitives). These theoretical results are validated by numerical experiments in standard non-convex test functions and large-scale traffic assignment problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge