A conditional gradient homotopy method with applications to Semidefinite Programming

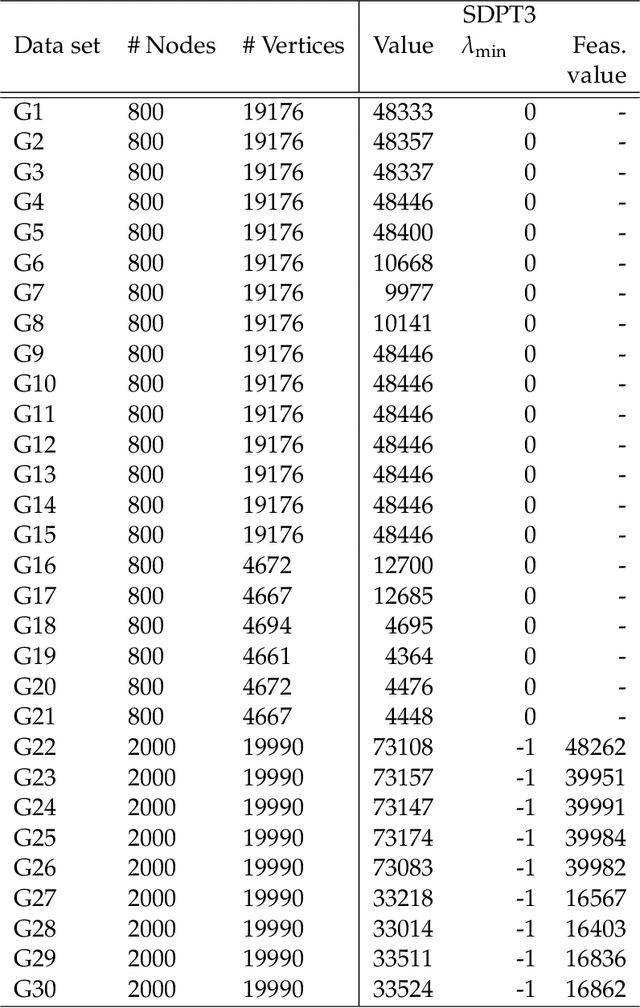
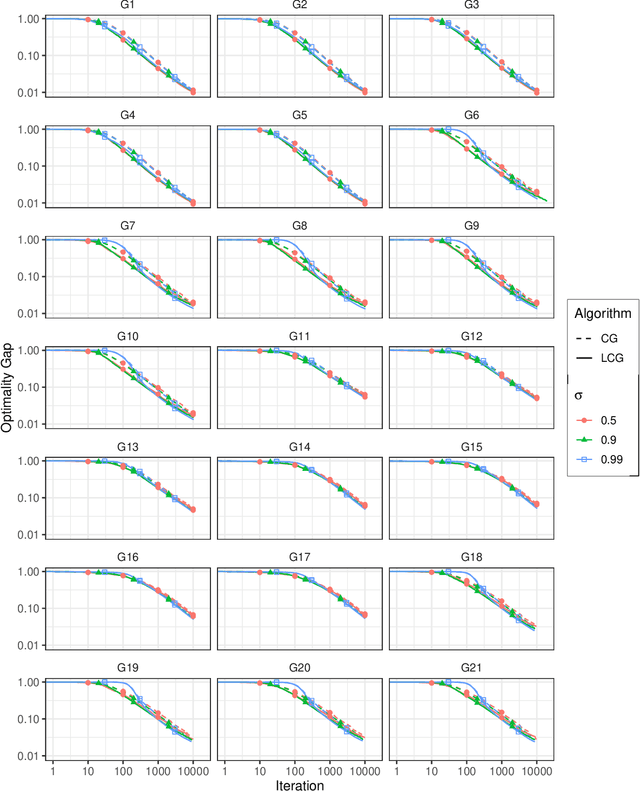
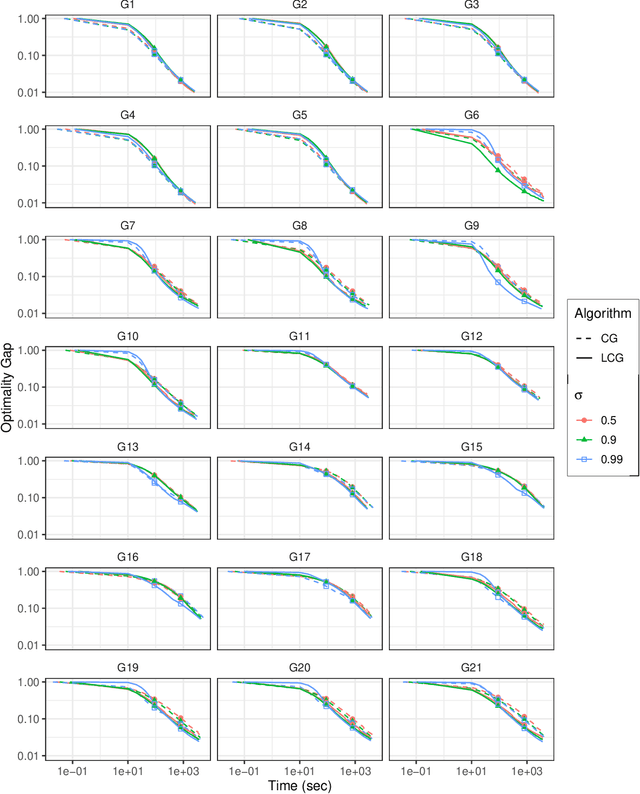
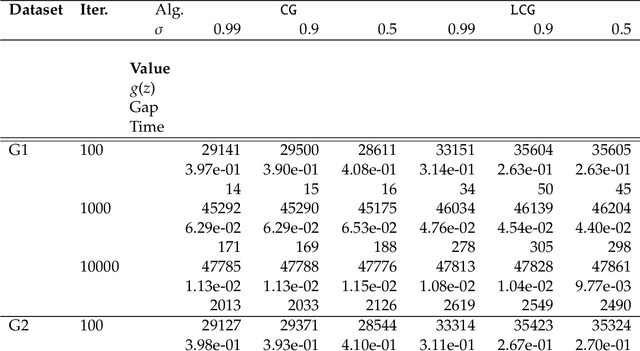
We propose a new homotopy-based conditional gradient method for solving convex optimization problems with a large number of simple conic constraints. Instances of this template naturally appear in semidefinite programming problems arising as convex relaxations of combinatorial optimization problems. Our method is a double-loop algorithm in which the conic constraint is treated via a self-concordant barrier, and the inner loop employs a conditional gradient algorithm to approximate the analytic central path, while the outer loop updates the accuracy imposed on the temporal solution and the homotopy parameter. Our theoretical iteration complexity is competitive when confronted to state-of-the-art SDP solvers, with the decisive advantage of cheap projection-free subroutines. Preliminary numerical experiments are provided for illustrating the practical performance of the method.

First-Order Methods for Convex Optimization

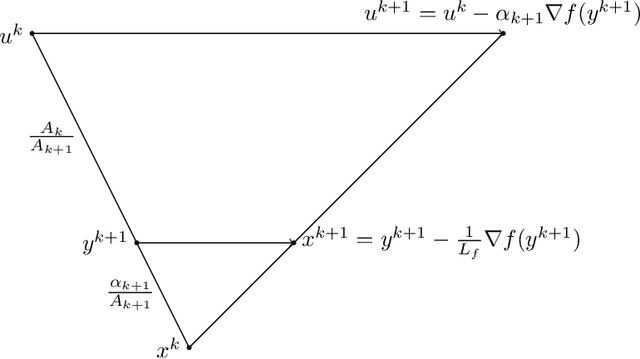
First-order methods for solving convex optimization problems have been at the forefront of mathematical optimization in the last 20 years. The rapid development of this important class of algorithms is motivated by the success stories reported in various applications, including most importantly machine learning, signal processing, imaging and control theory. First-order methods have the potential to provide low accuracy solutions at low computational complexity which makes them an attractive set of tools in large-scale optimization problems. In this survey we cover a number of key developments in gradient-based optimization methods. This includes non-Euclidean extensions of the classical proximal gradient method, and its accelerated versions. Additionally we survey recent developments within the class of projection-free methods, and proximal versions of primal-dual schemes. We give complete proofs for various key results, and highlight the unifying aspects of several optimization algorithms.

Self-concordant analysis of Frank-Wolfe algorithms

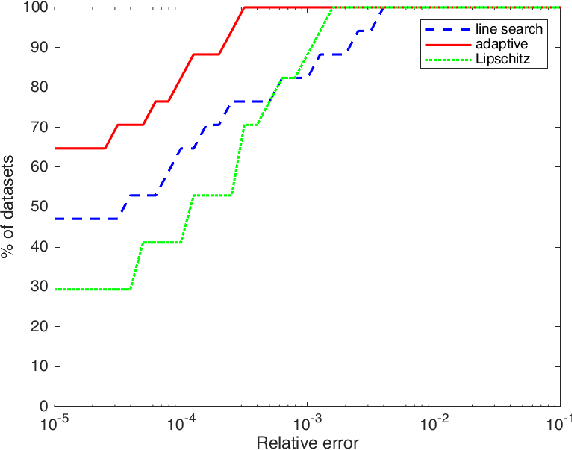
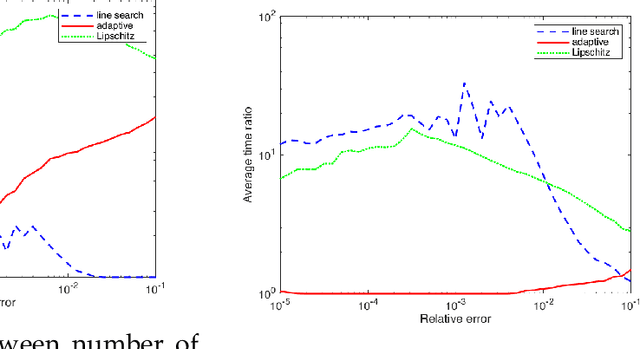
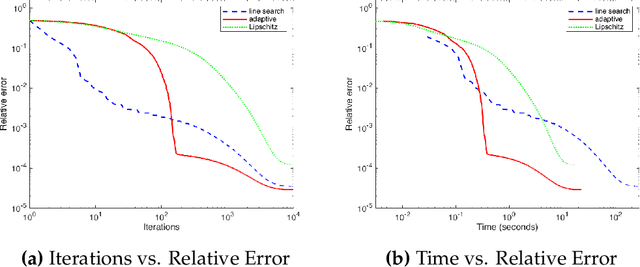
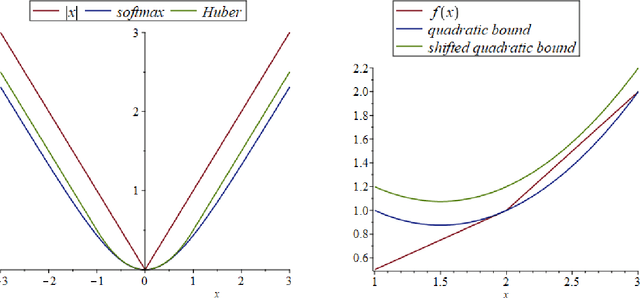
Projection-free optimization via different variants of the Frank-Wolfe (FW) method has become one of the cornerstones in optimization for machine learning since in many cases the linear minimization oracle is much cheaper to implement than projections and some sparsity needs to be preserved. In a number of applications, e.g. Poisson inverse problems or quantum state tomography, the loss is given by a self-concordant (SC) function having unbounded curvature, implying absence of theoretical guarantees for the existing FW methods. We use the theory of SC functions to provide a new adaptive step size for FW methods and prove global convergence rate O(1/k), k being the iteration counter. If the problem can be represented by a local linear minimization oracle, we are the first to propose a FW method with linear convergence rate without assuming neither strong convexity nor a Lipschitz continuous gradient.