Interaction-Force Transport Gradient Flows

This paper presents a new type of gradient flow geometries over non-negative and probability measures motivated via a principled construction that combines the optimal transport and interaction forces modeled by reproducing kernels. Concretely, we propose the interaction-force transport (IFT) gradient flows and its spherical variant via an infimal convolution of the Wasserstein and spherical MMD Riemannian metric tensors. We then develop a particle-based optimization algorithm based on the JKO-splitting scheme of the mass-preserving spherical IFT gradient flows. Finally, we provide both theoretical global exponential convergence guarantees and empirical simulation results for applying the IFT gradient flows to the sampling task of MMD-minimization studied by Arbel et al. [2019]. Furthermore, we prove that the spherical IFT gradient flow enjoys the best of both worlds by providing the global exponential convergence guarantee for both the MMD and KL energy.

Analysis of Kernel Mirror Prox for Measure Optimization

By choosing a suitable function space as the dual to the non-negative measure cone, we study in a unified framework a class of functional saddle-point optimization problems, which we term the Mixed Functional Nash Equilibrium (MFNE), that underlies several existing machine learning algorithms, such as implicit generative models, distributionally robust optimization (DRO), and Wasserstein barycenters. We model the saddle-point optimization dynamics as an interacting Fisher-Rao-RKHS gradient flow when the function space is chosen as a reproducing kernel Hilbert space (RKHS). As a discrete time counterpart, we propose a primal-dual kernel mirror prox (KMP) algorithm, which uses a dual step in the RKHS, and a primal entropic mirror prox step. We then provide a unified convergence analysis of KMP in an infinite-dimensional setting for this class of MFNE problems, which establishes a convergence rate of $O(1/N)$ in the deterministic case and $O(1/\sqrt{N})$ in the stochastic case, where $N$ is the iteration counter. As a case study, we apply our analysis to DRO, providing algorithmic guarantees for DRO robustness and convergence.

High-Probability Convergence for Composite and Distributed Stochastic Minimization and Variational Inequalities with Heavy-Tailed Noise

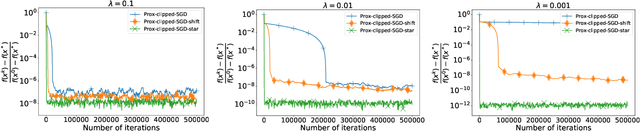
High-probability analysis of stochastic first-order optimization methods under mild assumptions on the noise has been gaining a lot of attention in recent years. Typically, gradient clipping is one of the key algorithmic ingredients to derive good high-probability guarantees when the noise is heavy-tailed. However, if implemented na\"ively, clipping can spoil the convergence of the popular methods for composite and distributed optimization (Prox-SGD/Parallel SGD) even in the absence of any noise. Due to this reason, many works on high-probability analysis consider only unconstrained non-distributed problems, and the existing results for composite/distributed problems do not include some important special cases (like strongly convex problems) and are not optimal. To address this issue, we propose new stochastic methods for composite and distributed optimization based on the clipping of stochastic gradient differences and prove tight high-probability convergence results (including nearly optimal ones) for the new methods. Using similar ideas, we also develop new methods for composite and distributed variational inequalities and analyze the high-probability convergence of these methods.

High-Probability Bounds for Stochastic Optimization and Variational Inequalities: the Case of Unbounded Variance

During recent years the interest of optimization and machine learning communities in high-probability convergence of stochastic optimization methods has been growing. One of the main reasons for this is that high-probability complexity bounds are more accurate and less studied than in-expectation ones. However, SOTA high-probability non-asymptotic convergence results are derived under strong assumptions such as the boundedness of the gradient noise variance or of the objective's gradient itself. In this paper, we propose several algorithms with high-probability convergence results under less restrictive assumptions. In particular, we derive new high-probability convergence results under the assumption that the gradient/operator noise has bounded central $\alpha$-th moment for $\alpha \in (1,2]$ in the following setups: (i) smooth non-convex / Polyak-Lojasiewicz / convex / strongly convex / quasi-strongly convex minimization problems, (ii) Lipschitz / star-cocoercive and monotone / quasi-strongly monotone variational inequalities. These results justify the usage of the considered methods for solving problems that do not fit standard functional classes studied in stochastic optimization.

A conditional gradient homotopy method with applications to Semidefinite Programming

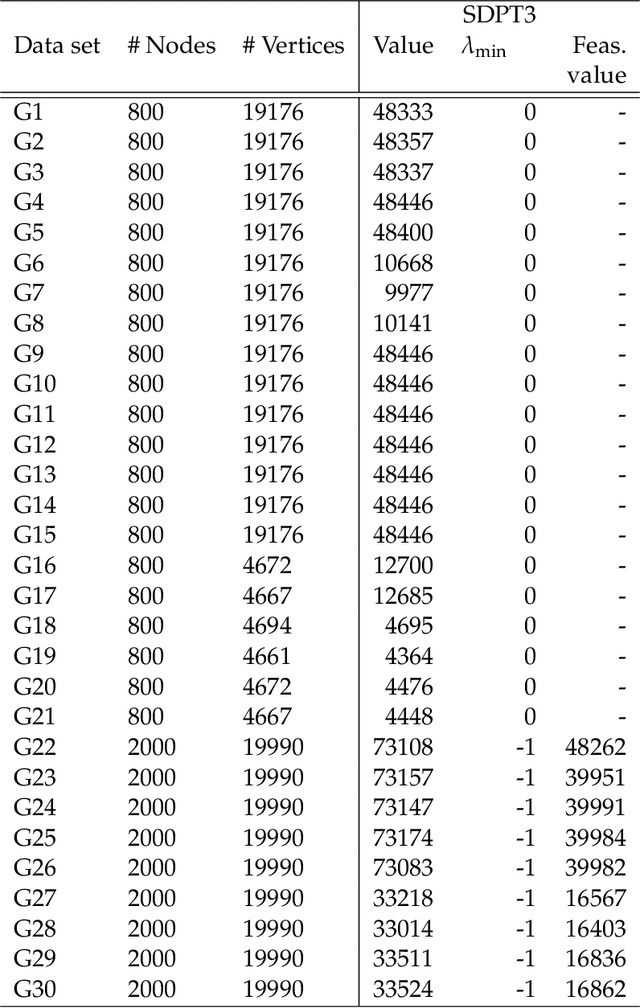
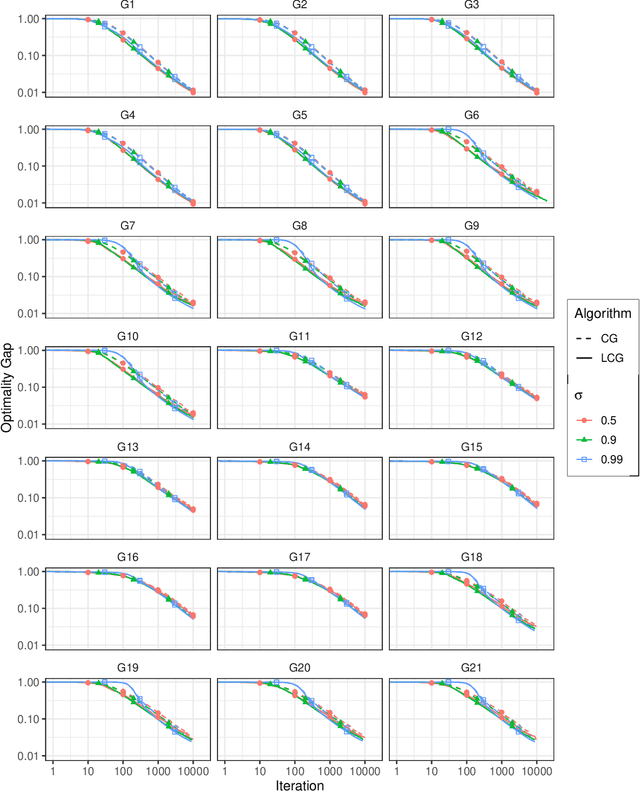
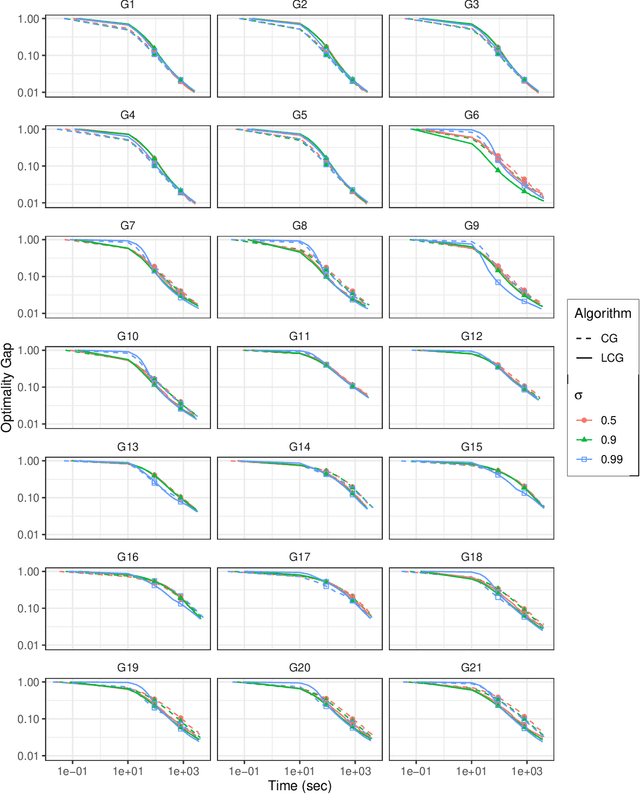
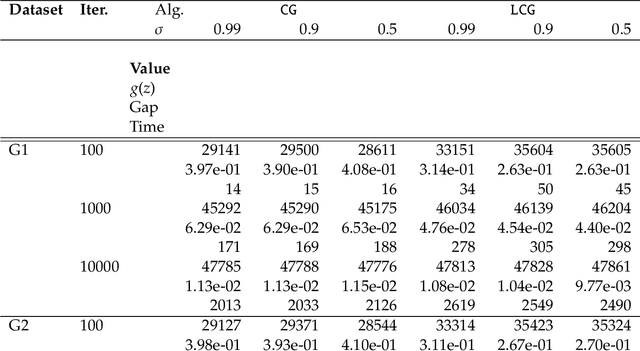
We propose a new homotopy-based conditional gradient method for solving convex optimization problems with a large number of simple conic constraints. Instances of this template naturally appear in semidefinite programming problems arising as convex relaxations of combinatorial optimization problems. Our method is a double-loop algorithm in which the conic constraint is treated via a self-concordant barrier, and the inner loop employs a conditional gradient algorithm to approximate the analytic central path, while the outer loop updates the accuracy imposed on the temporal solution and the homotopy parameter. Our theoretical iteration complexity is competitive when confronted to state-of-the-art SDP solvers, with the decisive advantage of cheap projection-free subroutines. Preliminary numerical experiments are provided for illustrating the practical performance of the method.

Clipped Stochastic Methods for Variational Inequalities with Heavy-Tailed Noise

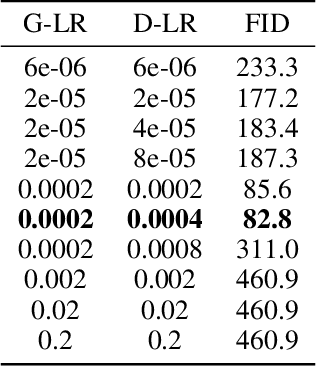
Stochastic first-order methods such as Stochastic Extragradient (SEG) or Stochastic Gradient Descent-Ascent (SGDA) for solving smooth minimax problems and, more generally, variational inequality problems (VIP) have been gaining a lot of attention in recent years due to the growing popularity of adversarial formulations in machine learning. However, while high-probability convergence bounds are known to reflect the actual behavior of stochastic methods more accurately, most convergence results are provided in expectation. Moreover, the only known high-probability complexity results have been derived under restrictive sub-Gaussian (light-tailed) noise and bounded domain Assump. [Juditsky et al., 2011]. In this work, we prove the first high-probability complexity results with logarithmic dependence on the confidence level for stochastic methods for solving monotone and structured non-monotone VIPs with non-sub-Gaussian (heavy-tailed) noise and unbounded domains. In the monotone case, our results match the best-known ones in the light-tails case [Juditsky et al., 2011], and are novel for structured non-monotone problems such as negative comonotone, quasi-strongly monotone, and/or star-cocoercive ones. We achieve these results by studying SEG and SGDA with clipping. In addition, we numerically validate that the gradient noise of many practical GAN formulations is heavy-tailed and show that clipping improves the performance of SEG/SGDA.

Decentralized Local Stochastic Extra-Gradient for Variational Inequalities

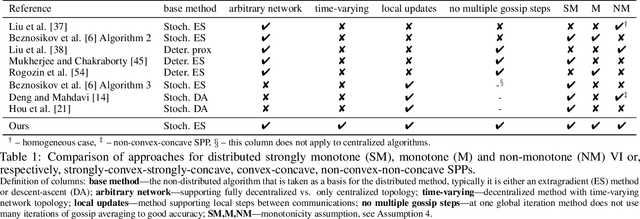
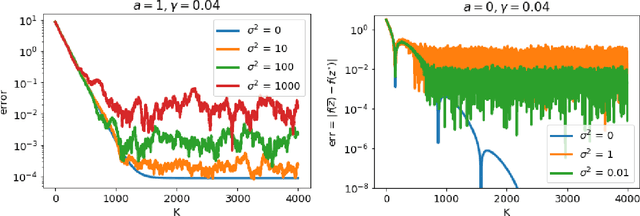
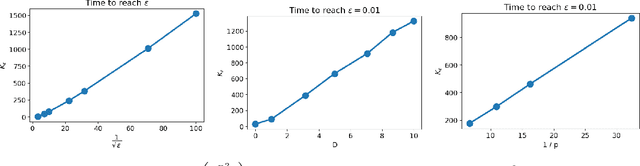
We consider decentralized stochastic variational inequalities where the problem data is distributed across many participating devices (heterogeneous, or non-IID data setting). We propose a novel method - based on stochastic extra-gradient - where participating devices can communicate over arbitrary, possibly time-varying network topologies. This covers both the fully decentralized optimization setting and the centralized topologies commonly used in Federated Learning. Our method further supports multiple local updates on the workers for reducing the communication frequency between workers. We theoretically analyze the proposed scheme in the strongly monotone, monotone and non-monotone setting. As a special case, our method and analysis apply in particular to decentralized stochastic min-max problems which are being studied with increased interest in Deep Learning. For example, the training objective of Generative Adversarial Networks (GANs) are typically saddle point problems and the decentralized training of GANs has been reported to be extremely challenging. While SOTA techniques rely on either repeated gossip rounds or proximal updates, we alleviate both of these requirements. Experimental results for decentralized GAN demonstrate the effectiveness of our proposed algorithm.

Near-Optimal High Probability Complexity Bounds for Non-Smooth Stochastic Optimization with Heavy-Tailed Noise

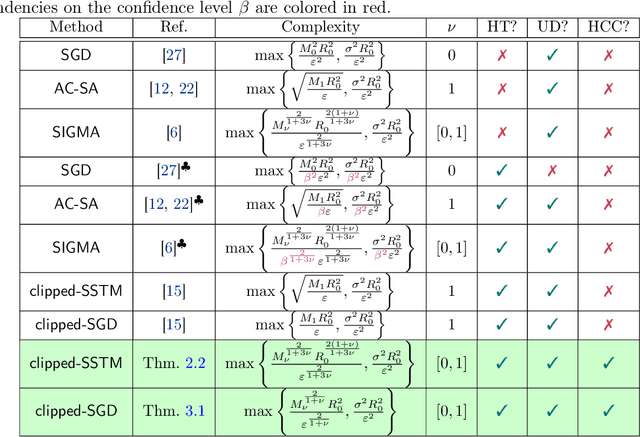
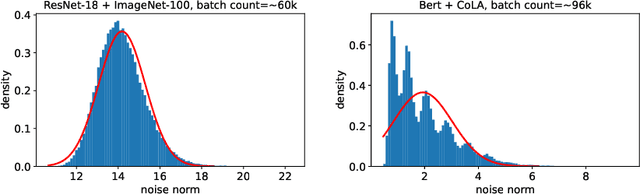
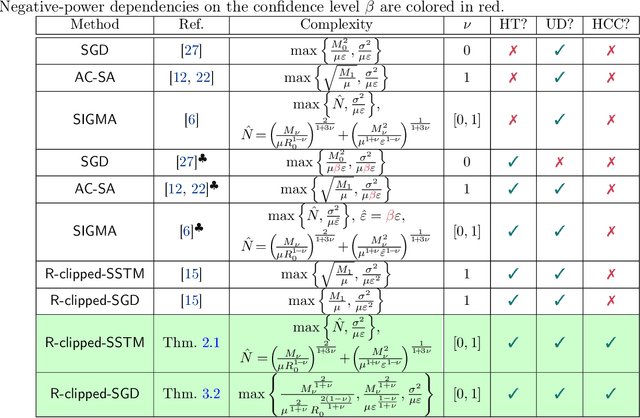
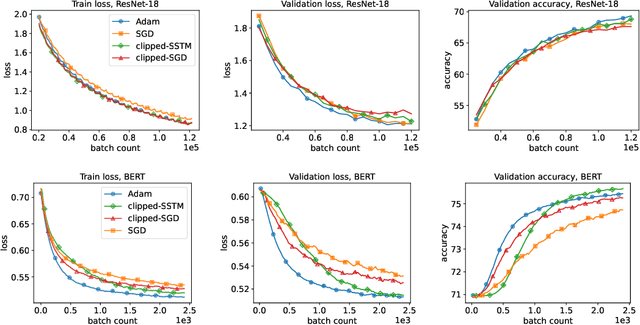
Thanks to their practical efficiency and random nature of the data, stochastic first-order methods are standard for training large-scale machine learning models. Random behavior may cause a particular run of an algorithm to result in a highly suboptimal objective value, whereas theoretical guarantees are usually proved for the expectation of the objective value. Thus, it is essential to theoretically guarantee that algorithms provide small objective residual with high probability. Existing methods for non-smooth stochastic convex optimization have complexity bounds with the dependence on the confidence level that is either negative-power or logarithmic but under an additional assumption of sub-Gaussian (light-tailed) noise distribution that may not hold in practice, e.g., in several NLP tasks. In our paper, we resolve this issue and derive the first high-probability convergence results with logarithmic dependence on the confidence level for non-smooth convex stochastic optimization problems with non-sub-Gaussian (heavy-tailed) noise. To derive our results, we propose novel stepsize rules for two stochastic methods with gradient clipping. Moreover, our analysis works for generalized smooth objectives with H\"older-continuous gradients, and for both methods, we provide an extension for strongly convex problems. Finally, our results imply that the first (accelerated) method we consider also has optimal iteration and oracle complexity in all the regimes, and the second one is optimal in the non-smooth setting.

First-Order Methods for Convex Optimization

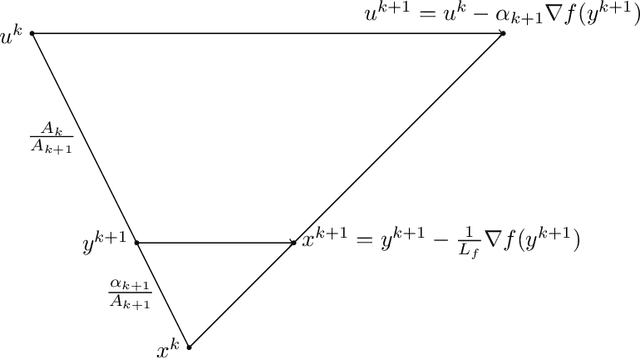
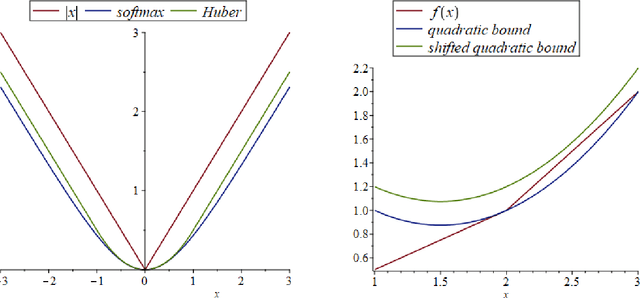
First-order methods for solving convex optimization problems have been at the forefront of mathematical optimization in the last 20 years. The rapid development of this important class of algorithms is motivated by the success stories reported in various applications, including most importantly machine learning, signal processing, imaging and control theory. First-order methods have the potential to provide low accuracy solutions at low computational complexity which makes them an attractive set of tools in large-scale optimization problems. In this survey we cover a number of key developments in gradient-based optimization methods. This includes non-Euclidean extensions of the classical proximal gradient method, and its accelerated versions. Additionally we survey recent developments within the class of projection-free methods, and proximal versions of primal-dual schemes. We give complete proofs for various key results, and highlight the unifying aspects of several optimization algorithms.

Recent Theoretical Advances in Non-Convex Optimization

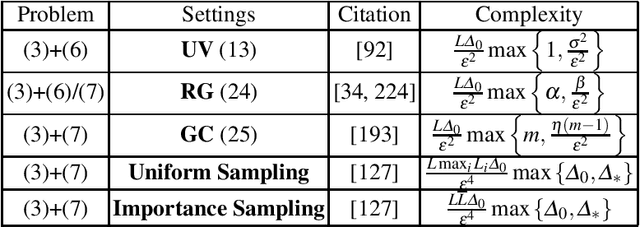
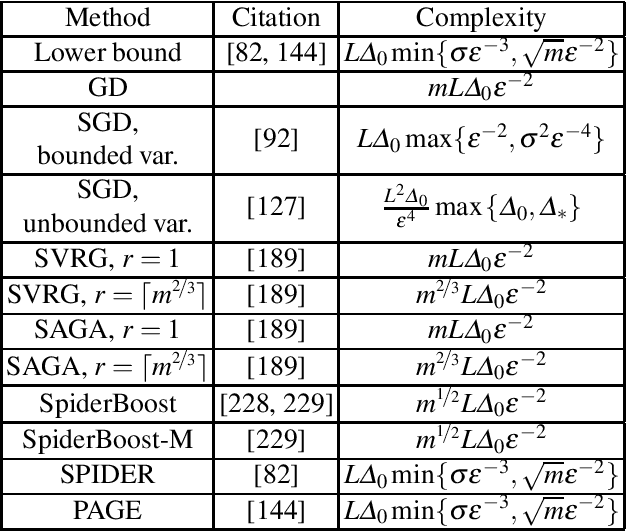
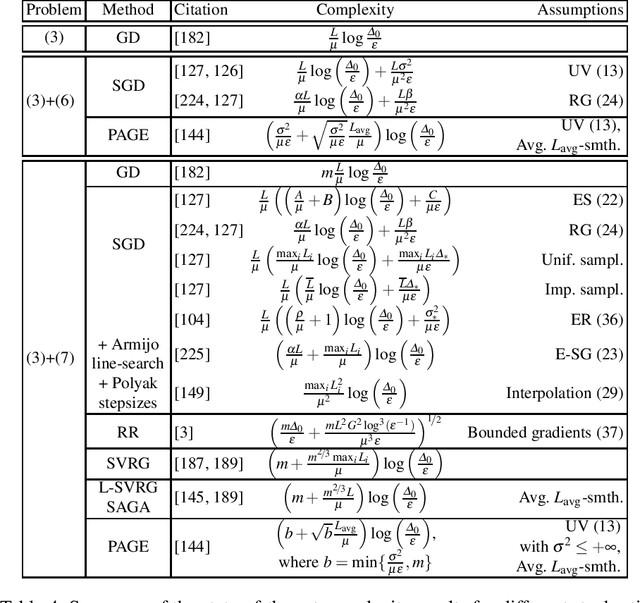
Motivated by recent increased interest in optimization algorithms for non-convex optimization in application to training deep neural networks and other optimization problems in data analysis, we give an overview of recent theoretical results on global performance guarantees of optimization algorithms for non-convex optimization. We start with classical arguments showing that general non-convex problems could not be solved efficiently in a reasonable time. Then we give a list of problems that can be solved efficiently to find the global minimizer by exploiting the structure of the problem as much as it is possible. Another way to deal with non-convexity is to relax the goal from finding the global minimum to finding a stationary point or a local minimum. For this setting, we first present known results for the convergence rates of deterministic first-order methods, which are then followed by a general theoretical analysis of optimal stochastic and randomized gradient schemes, and an overview of the stochastic first-order methods. After that, we discuss quite general classes of non-convex problems, such as minimization of $\alpha$-weakly-quasi-convex functions and functions that satisfy Polyak--Lojasiewicz condition, which still allow obtaining theoretical convergence guarantees of first-order methods. Then we consider higher-order and zeroth-order/derivative-free methods and their convergence rates for non-convex optimization problems.