Valentin Samokhin
M3DA: Benchmark for Unsupervised Domain Adaptation in 3D Medical Image Segmentation
Feb 24, 2025



Abstract:Domain shift presents a significant challenge in applying Deep Learning to the segmentation of 3D medical images from sources like Magnetic Resonance Imaging (MRI) and Computed Tomography (CT). Although numerous Domain Adaptation methods have been developed to address this issue, they are often evaluated under impractical data shift scenarios. Specifically, the medical imaging datasets used are often either private, too small for robust training and evaluation, or limited to single or synthetic tasks. To overcome these limitations, we introduce a M3DA /"mEd@/ benchmark comprising four publicly available, multiclass segmentation datasets. We have designed eight domain pairs featuring diverse and practically relevant distribution shifts. These include inter-modality shifts between MRI and CT and intra-modality shifts among various MRI acquisition parameters, different CT radiation doses, and presence/absence of contrast enhancement in images. Within the proposed benchmark, we evaluate more than ten existing domain adaptation methods. Our results show that none of them can consistently close the performance gap between the domains. For instance, the most effective method reduces the performance gap by about 62% across the tasks. This highlights the need for developing novel domain adaptation algorithms to enhance the robustness and scalability of deep learning models in medical imaging. We made our M3DA benchmark publicly available: https://github.com/BorisShirokikh/M3DA.
Anatomical Positional Embeddings
Sep 16, 2024Abstract:We propose a self-supervised model producing 3D anatomical positional embeddings (APE) of individual medical image voxels. APE encodes voxels' anatomical closeness, i.e., voxels of the same organ or nearby organs always have closer positional embeddings than the voxels of more distant body parts. In contrast to the existing models of anatomical positional embeddings, our method is able to efficiently produce a map of voxel-wise embeddings for a whole volumetric input image, which makes it an optimal choice for different downstream applications. We train our APE model on 8400 publicly available CT images of abdomen and chest regions. We demonstrate its superior performance compared with the existing models on anatomical landmark retrieval and weakly-supervised few-shot localization of 13 abdominal organs. As a practical application, we show how to cheaply train APE to crop raw CT images to different anatomical regions of interest with 0.99 recall, while reducing the image volume by 10-100 times. The code and the pre-trained APE model are available at https://github.com/mishgon/ape .
Robust Curve Detection in Volumetric Medical Imaging via Attraction Field
Aug 02, 2024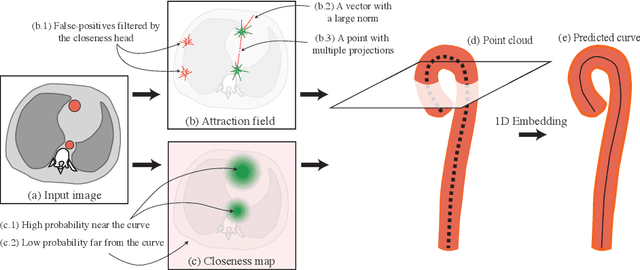
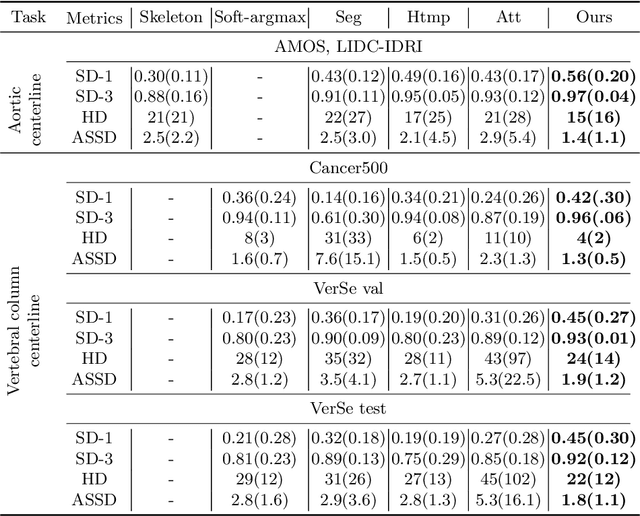
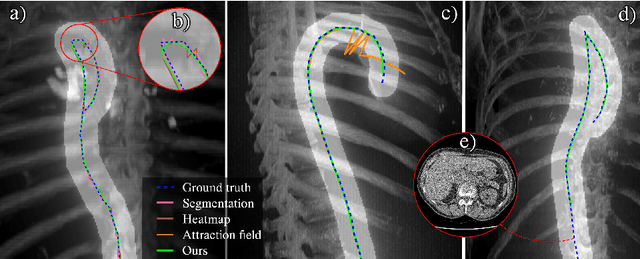
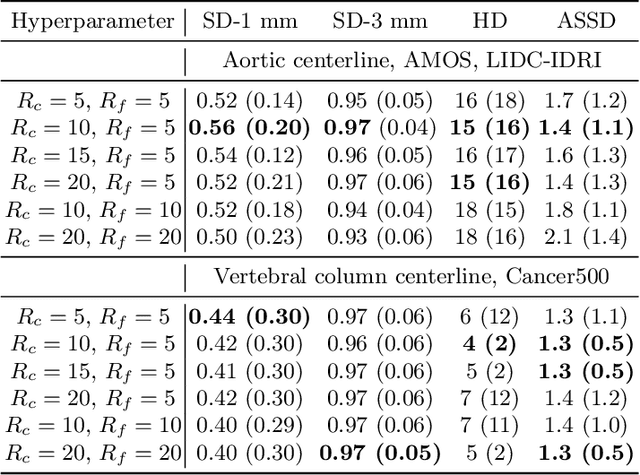
Abstract:Understanding body part geometry is crucial for precise medical diagnostics. Curves effectively describe anatomical structures and are widely used in medical imaging applications related to cardiovascular, respiratory, and skeletal diseases. Traditional curve detection methods are often task-specific, relying heavily on domain-specific features, limiting their broader applicability. This paper introduces a novel approach for detecting non-branching curves, which does not require prior knowledge of the object's orientation, shape, or position. Our method uses neural networks to predict (1) an attraction field, which offers subpixel accuracy, and (2) a closeness map, which limits the region of interest and essentially eliminates outliers far from the desired curve. We tested our curve detector on several clinically relevant tasks with diverse morphologies and achieved impressive subpixel-level accuracy results that surpass existing methods, highlighting its versatility and robustness. Additionally, to support further advancements in this field, we provide our private annotations of aortic centerlines and masks, which can serve as a benchmark for future research. The dataset can be found at https://github.com/neuro-ml/curve-detection.
The impact of deep learning aid on the workload and interpretation accuracy of radiologists on chest computed tomography: a cross-over reader study
Jun 12, 2024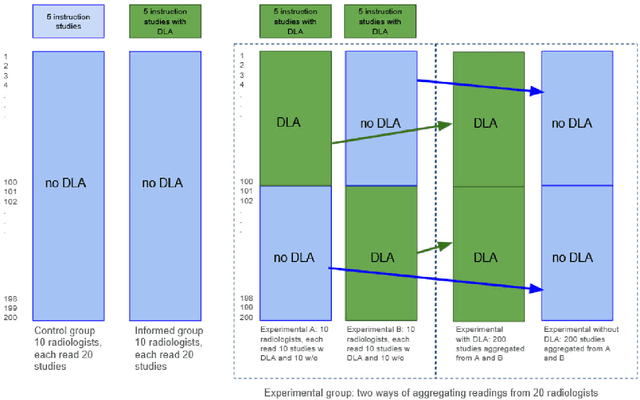
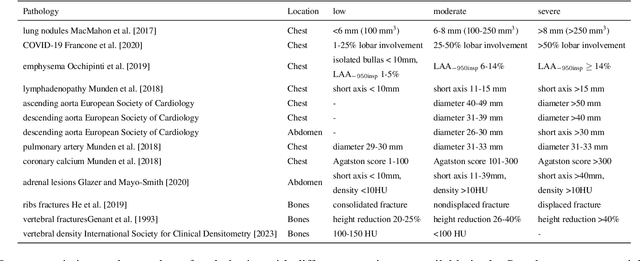
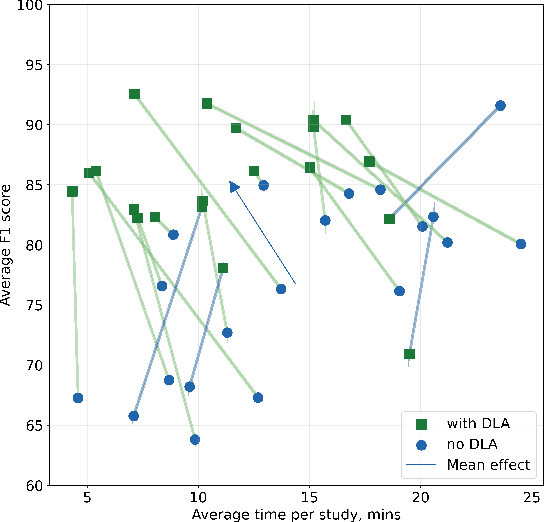
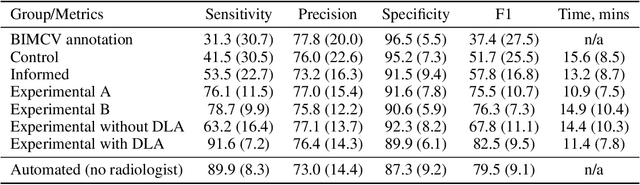
Abstract:Interpretation of chest computed tomography (CT) is time-consuming. Previous studies have measured the time-saving effect of using a deep-learning-based aid (DLA) for CT interpretation. We evaluated the joint impact of a multi-pathology DLA on the time and accuracy of radiologists' reading. 40 radiologists were randomly split into three experimental arms: control (10), who interpret studies without assistance; informed group (10), who were briefed about DLA pathologies, but performed readings without it; and the experimental group (20), who interpreted half studies with DLA, and half without. Every arm used the same 200 CT studies retrospectively collected from BIMCV-COVID19 dataset; each radiologist provided readings for 20 CT studies. We compared interpretation time, and accuracy of participants diagnostic report with respect to 12 pathological findings. Mean reading time per study was 15.6 minutes [SD 8.5] in the control arm, 13.2 minutes [SD 8.7] in the informed arm, 14.4 [SD 10.3] in the experimental arm without DLA, and 11.4 minutes [SD 7.8] in the experimental arm with DLA. Mean sensitivity and specificity were 41.5 [SD 30.4], 86.8 [SD 28.3] in the control arm; 53.5 [SD 22.7], 92.3 [SD 9.4] in the informed non-assisted arm; 63.2 [SD 16.4], 92.3 [SD 8.2] in the experimental arm without DLA; and 91.6 [SD 7.2], 89.9 [SD 6.0] in the experimental arm with DLA. DLA speed up interpretation time per study by 2.9 minutes (CI95 [1.7, 4.3], p<0.0005), increased sensitivity by 28.4 (CI95 [23.4, 33.4], p<0.0005), and decreased specificity by 2.4 (CI95 [0.6, 4.3], p=0.13). Of 20 radiologists in the experimental arm, 16 have improved reading time and sensitivity, two improved their time with a marginal drop in sensitivity, and two participants improved sensitivity with increased time. Overall, DLA introduction decreased reading time by 20.6%.
Decentralized Local Stochastic Extra-Gradient for Variational Inequalities
Jun 15, 2021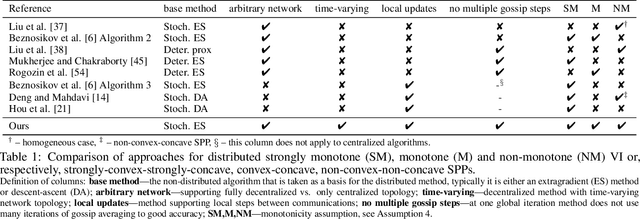
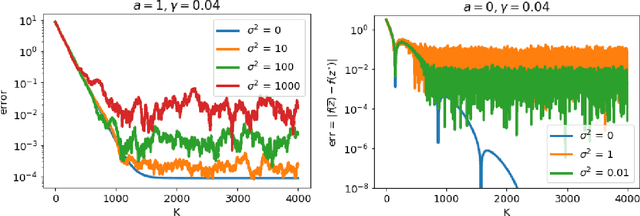
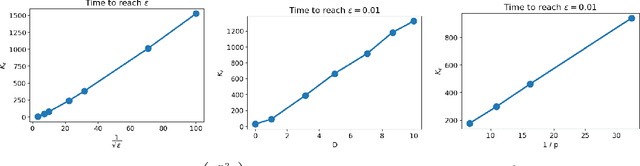
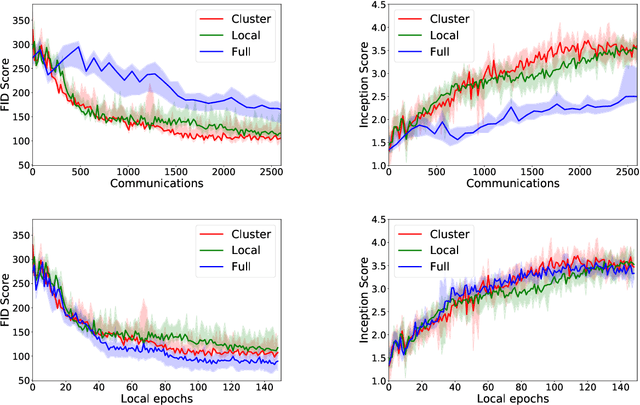
Abstract:We consider decentralized stochastic variational inequalities where the problem data is distributed across many participating devices (heterogeneous, or non-IID data setting). We propose a novel method - based on stochastic extra-gradient - where participating devices can communicate over arbitrary, possibly time-varying network topologies. This covers both the fully decentralized optimization setting and the centralized topologies commonly used in Federated Learning. Our method further supports multiple local updates on the workers for reducing the communication frequency between workers. We theoretically analyze the proposed scheme in the strongly monotone, monotone and non-monotone setting. As a special case, our method and analysis apply in particular to decentralized stochastic min-max problems which are being studied with increased interest in Deep Learning. For example, the training objective of Generative Adversarial Networks (GANs) are typically saddle point problems and the decentralized training of GANs has been reported to be extremely challenging. While SOTA techniques rely on either repeated gossip rounds or proximal updates, we alleviate both of these requirements. Experimental results for decentralized GAN demonstrate the effectiveness of our proposed algorithm.
Local SGD for Saddle-Point Problems
Oct 25, 2020
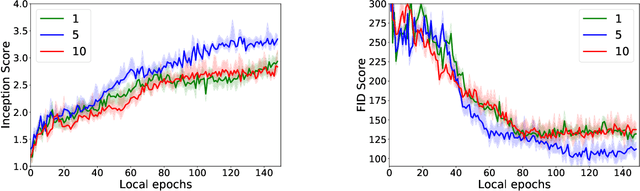

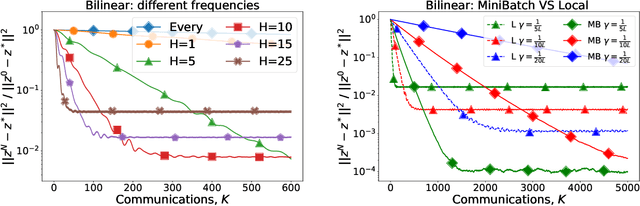
Abstract:GAN is one of the most popular and commonly used neural network models. When the model is large and there is a lot of data, the learning process can be delayed. The standard way out is to use multiple devices. Therefore, the methods of distributed and federated training for GANs are an important question. But from an optimization point of view, GANs are nothing more than a classical saddle-point problem: $\min_x \max_y f(x,y)$. Therefore, this paper focuses on the distributed optimization of the smooth stochastic saddle-point problems using Local SGD. We present a new algorithm specifically for our problem -- Extra Step Local SGD. The obtained theoretical bounds of communication rounds are $\Omega(K^{2/3} M^{1/3})$ in strongly-convex-strongly-concave case and $\Omega(K^{8/9} M^{4/9})$ in convex-concave (here $M$ -- number of functions (nodes) and $K$ - number of iterations).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge