Local SGD for Saddle-Point Problems
Paper and Code
Oct 25, 2020
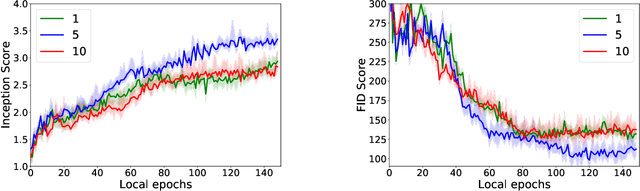

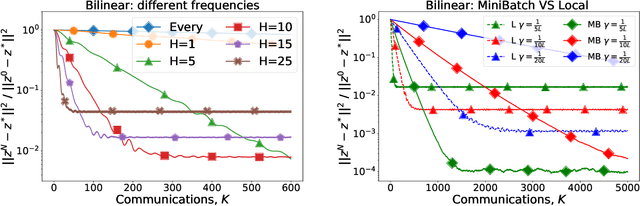
GAN is one of the most popular and commonly used neural network models. When the model is large and there is a lot of data, the learning process can be delayed. The standard way out is to use multiple devices. Therefore, the methods of distributed and federated training for GANs are an important question. But from an optimization point of view, GANs are nothing more than a classical saddle-point problem: $\min_x \max_y f(x,y)$. Therefore, this paper focuses on the distributed optimization of the smooth stochastic saddle-point problems using Local SGD. We present a new algorithm specifically for our problem -- Extra Step Local SGD. The obtained theoretical bounds of communication rounds are $\Omega(K^{2/3} M^{1/3})$ in strongly-convex-strongly-concave case and $\Omega(K^{8/9} M^{4/9})$ in convex-concave (here $M$ -- number of functions (nodes) and $K$ - number of iterations).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge