Near-Optimal High Probability Complexity Bounds for Non-Smooth Stochastic Optimization with Heavy-Tailed Noise

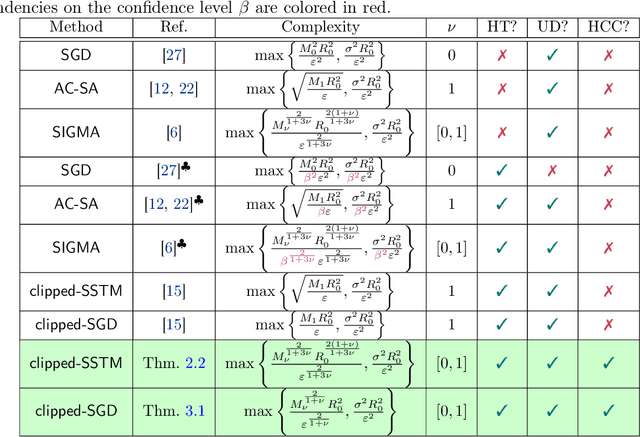
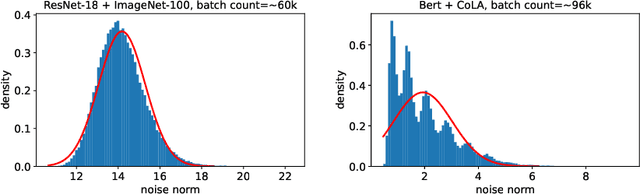
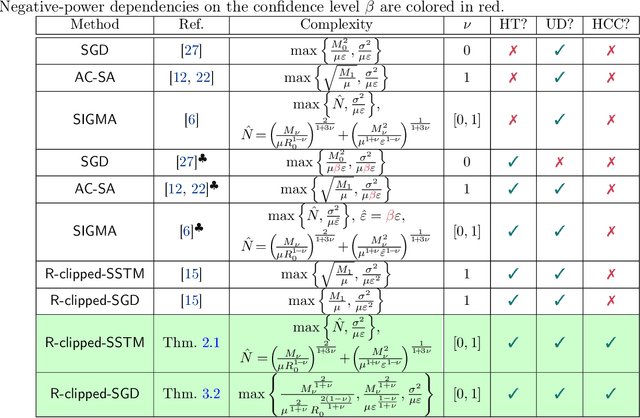
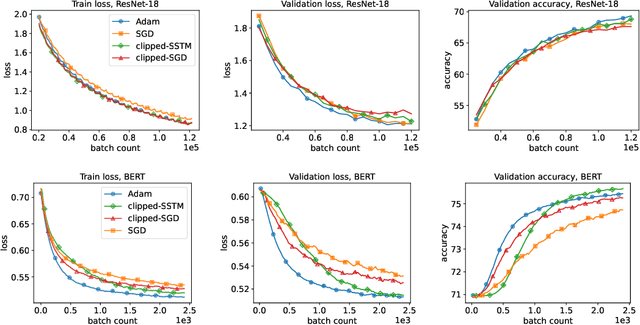
Thanks to their practical efficiency and random nature of the data, stochastic first-order methods are standard for training large-scale machine learning models. Random behavior may cause a particular run of an algorithm to result in a highly suboptimal objective value, whereas theoretical guarantees are usually proved for the expectation of the objective value. Thus, it is essential to theoretically guarantee that algorithms provide small objective residual with high probability. Existing methods for non-smooth stochastic convex optimization have complexity bounds with the dependence on the confidence level that is either negative-power or logarithmic but under an additional assumption of sub-Gaussian (light-tailed) noise distribution that may not hold in practice, e.g., in several NLP tasks. In our paper, we resolve this issue and derive the first high-probability convergence results with logarithmic dependence on the confidence level for non-smooth convex stochastic optimization problems with non-sub-Gaussian (heavy-tailed) noise. To derive our results, we propose novel stepsize rules for two stochastic methods with gradient clipping. Moreover, our analysis works for generalized smooth objectives with H\"older-continuous gradients, and for both methods, we provide an extension for strongly convex problems. Finally, our results imply that the first (accelerated) method we consider also has optimal iteration and oracle complexity in all the regimes, and the second one is optimal in the non-smooth setting.

Recent Theoretical Advances in Non-Convex Optimization

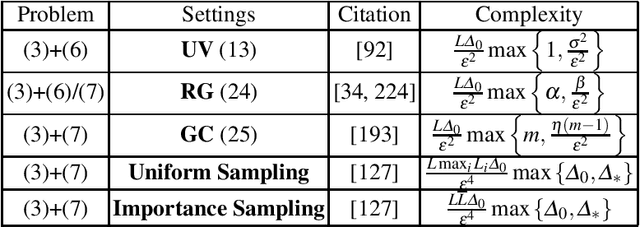
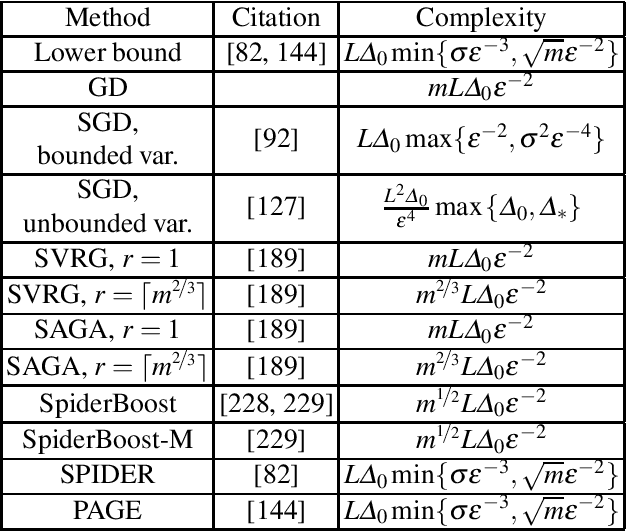
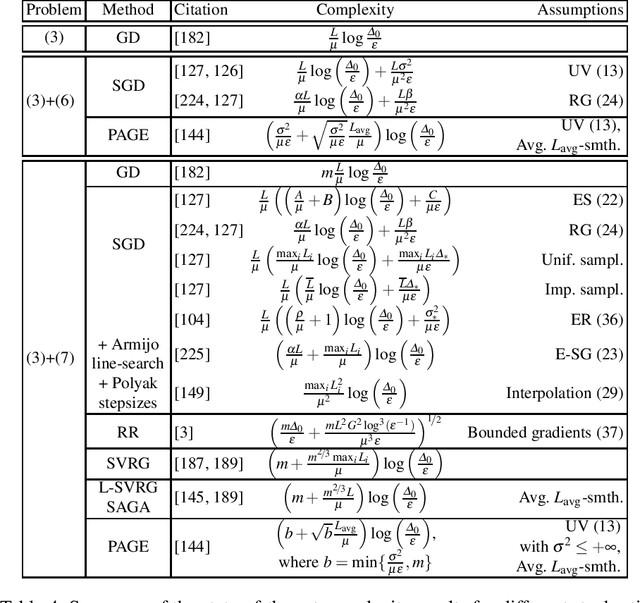
Motivated by recent increased interest in optimization algorithms for non-convex optimization in application to training deep neural networks and other optimization problems in data analysis, we give an overview of recent theoretical results on global performance guarantees of optimization algorithms for non-convex optimization. We start with classical arguments showing that general non-convex problems could not be solved efficiently in a reasonable time. Then we give a list of problems that can be solved efficiently to find the global minimizer by exploiting the structure of the problem as much as it is possible. Another way to deal with non-convexity is to relax the goal from finding the global minimum to finding a stationary point or a local minimum. For this setting, we first present known results for the convergence rates of deterministic first-order methods, which are then followed by a general theoretical analysis of optimal stochastic and randomized gradient schemes, and an overview of the stochastic first-order methods. After that, we discuss quite general classes of non-convex problems, such as minimization of $\alpha$-weakly-quasi-convex functions and functions that satisfy Polyak--Lojasiewicz condition, which still allow obtaining theoretical convergence guarantees of first-order methods. Then we consider higher-order and zeroth-order/derivative-free methods and their convergence rates for non-convex optimization problems.