$ψ$DAG: Projected Stochastic Approximation Iteration for DAG Structure Learning

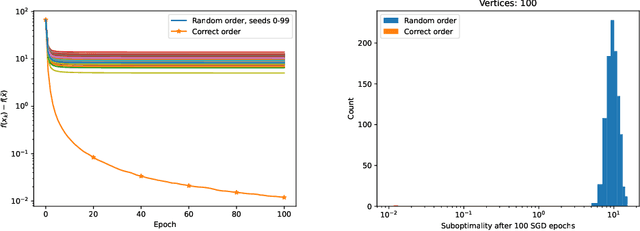
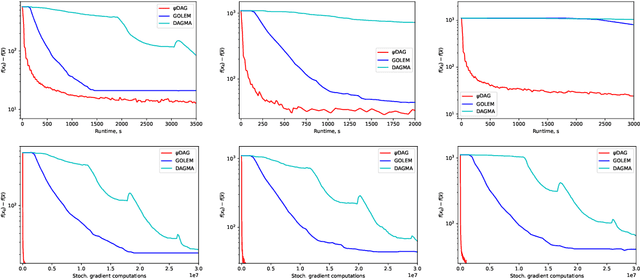
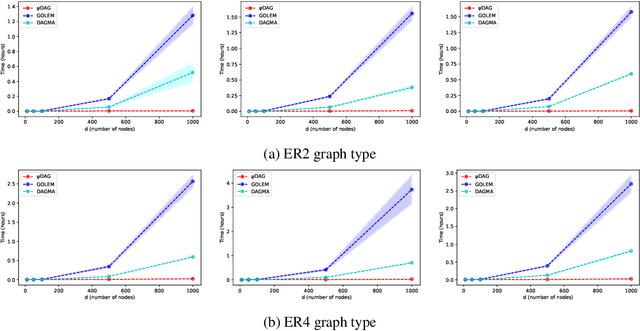
Learning the structure of Directed Acyclic Graphs (DAGs) presents a significant challenge due to the vast combinatorial search space of possible graphs, which scales exponentially with the number of nodes. Recent advancements have redefined this problem as a continuous optimization task by incorporating differentiable acyclicity constraints. These methods commonly rely on algebraic characterizations of DAGs, such as matrix exponentials, to enable the use of gradient-based optimization techniques. Despite these innovations, existing methods often face optimization difficulties due to the highly non-convex nature of DAG constraints and the per-iteration computational complexity. In this work, we present a novel framework for learning DAGs, employing a Stochastic Approximation approach integrated with Stochastic Gradient Descent (SGD)-based optimization techniques. Our framework introduces new projection methods tailored to efficiently enforce DAG constraints, ensuring that the algorithm converges to a feasible local minimum. With its low iteration complexity, the proposed method is well-suited for handling large-scale problems with improved computational efficiency. We demonstrate the effectiveness and scalability of our framework through comprehensive experimental evaluations, which confirm its superior performance across various settings.

AdaBatchGrad: Combining Adaptive Batch Size and Adaptive Step Size

This paper presents a novel adaptation of the Stochastic Gradient Descent (SGD), termed AdaBatchGrad. This modification seamlessly integrates an adaptive step size with an adjustable batch size. An increase in batch size and a decrease in step size are well-known techniques to tighten the area of convergence of SGD and decrease its variance. A range of studies by R. Byrd and J. Nocedal introduced various testing techniques to assess the quality of mini-batch gradient approximations and choose the appropriate batch sizes at every step. Methods that utilized exact tests were observed to converge within $O(LR^2/\varepsilon)$ iterations. Conversely, inexact test implementations sometimes resulted in non-convergence and erratic performance. To address these challenges, AdaBatchGrad incorporates both adaptive batch and step sizes, enhancing the method's robustness and stability. For exact tests, our approach converges in $O(LR^2/\varepsilon)$ iterations, analogous to standard gradient descent. For inexact tests, it achieves convergence in $O(\max\lbrace LR^2/\varepsilon, \sigma^2 R^2/\varepsilon^2 \rbrace )$ iterations. This makes AdaBatchGrad markedly more robust and computationally efficient relative to prevailing methods. To substantiate the efficacy of our method, we experimentally show, how the introduction of adaptive step size and adaptive batch size gradually improves the performance of regular SGD. The results imply that AdaBatchGrad surpasses alternative methods, especially when applied to inexact tests.

SANIA: Polyak-type Optimization Framework Leads to Scale Invariant Stochastic Algorithms

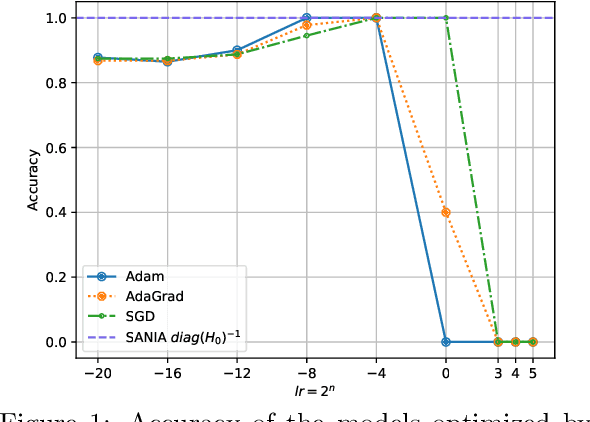
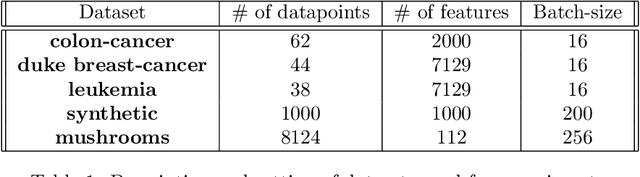
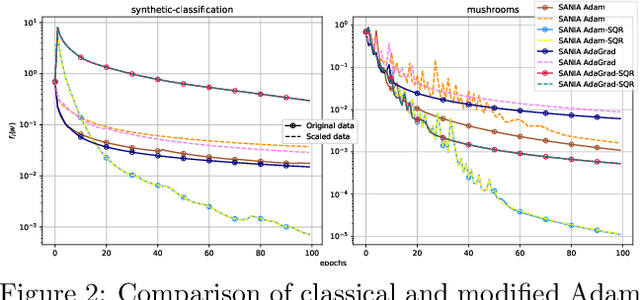
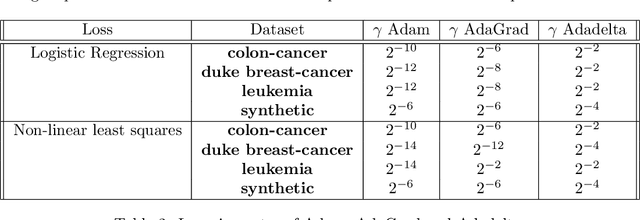
Adaptive optimization methods are widely recognized as among the most popular approaches for training Deep Neural Networks (DNNs). Techniques such as Adam, AdaGrad, and AdaHessian utilize a preconditioner that modifies the search direction by incorporating information about the curvature of the objective function. However, despite their adaptive characteristics, these methods still require manual fine-tuning of the step-size. This, in turn, impacts the time required to solve a particular problem. This paper presents an optimization framework named SANIA to tackle these challenges. Beyond eliminating the need for manual step-size hyperparameter settings, SANIA incorporates techniques to address poorly scaled or ill-conditioned problems. We also explore several preconditioning methods, including Hutchinson's method, which approximates the Hessian diagonal of the loss function. We conclude with an extensive empirical examination of the proposed techniques across classification tasks, covering both convex and non-convex contexts.

Stochastic Gradient Descent with Preconditioned Polyak Step-size

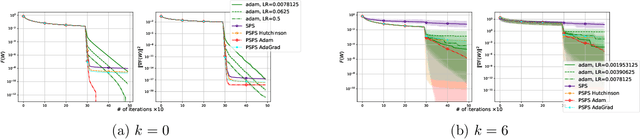
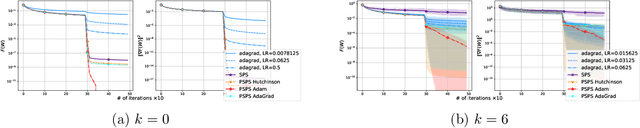
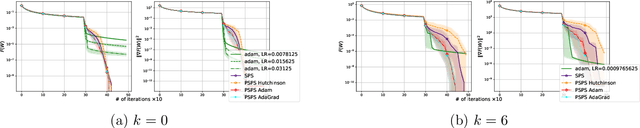
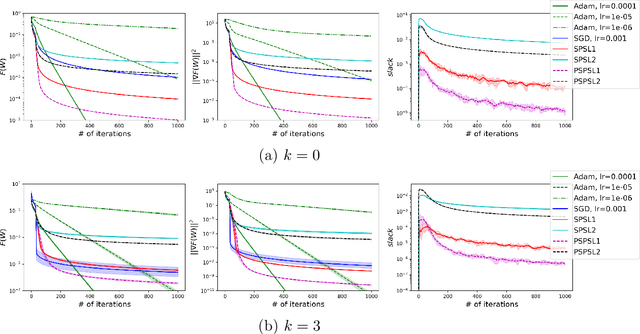
Stochastic Gradient Descent (SGD) is one of the many iterative optimization methods that are widely used in solving machine learning problems. These methods display valuable properties and attract researchers and industrial machine learning engineers with their simplicity. However, one of the weaknesses of this type of methods is the necessity to tune learning rate (step-size) for every loss function and dataset combination to solve an optimization problem and get an efficient performance in a given time budget. Stochastic Gradient Descent with Polyak Step-size (SPS) is a method that offers an update rule that alleviates the need of fine-tuning the learning rate of an optimizer. In this paper, we propose an extension of SPS that employs preconditioning techniques, such as Hutchinson's method, Adam, and AdaGrad, to improve its performance on badly scaled and/or ill-conditioned datasets.

Suppressing Poisoning Attacks on Federated Learning for Medical Imaging

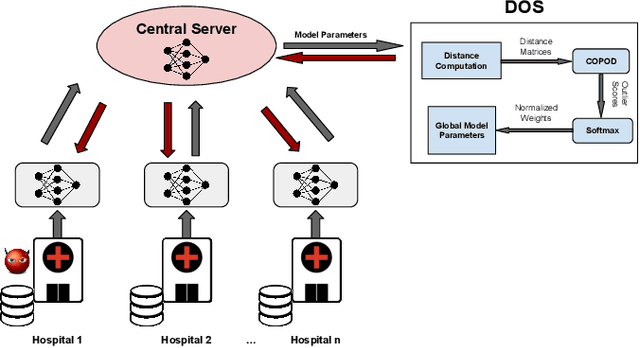
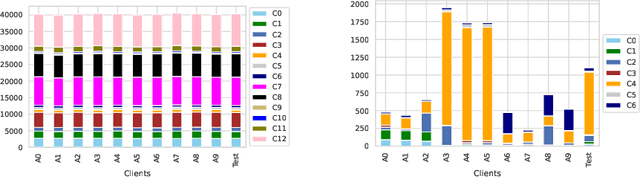
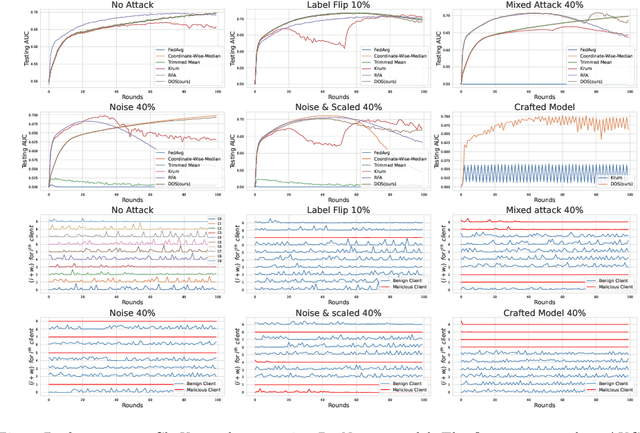
Collaboration among multiple data-owning entities (e.g., hospitals) can accelerate the training process and yield better machine learning models due to the availability and diversity of data. However, privacy concerns make it challenging to exchange data while preserving confidentiality. Federated Learning (FL) is a promising solution that enables collaborative training through exchange of model parameters instead of raw data. However, most existing FL solutions work under the assumption that participating clients are \emph{honest} and thus can fail against poisoning attacks from malicious parties, whose goal is to deteriorate the global model performance. In this work, we propose a robust aggregation rule called Distance-based Outlier Suppression (DOS) that is resilient to byzantine failures. The proposed method computes the distance between local parameter updates of different clients and obtains an outlier score for each client using Copula-based Outlier Detection (COPOD). The resulting outlier scores are converted into normalized weights using a softmax function, and a weighted average of the local parameters is used for updating the global model. DOS aggregation can effectively suppress parameter updates from malicious clients without the need for any hyperparameter selection, even when the data distributions are heterogeneous. Evaluation on two medical imaging datasets (CheXpert and HAM10000) demonstrates the higher robustness of DOS method against a variety of poisoning attacks in comparison to other state-of-the-art methods. The code can be found here https://github.com/Naiftt/SPAFD.

Stochastic Gradient Methods with Preconditioned Updates

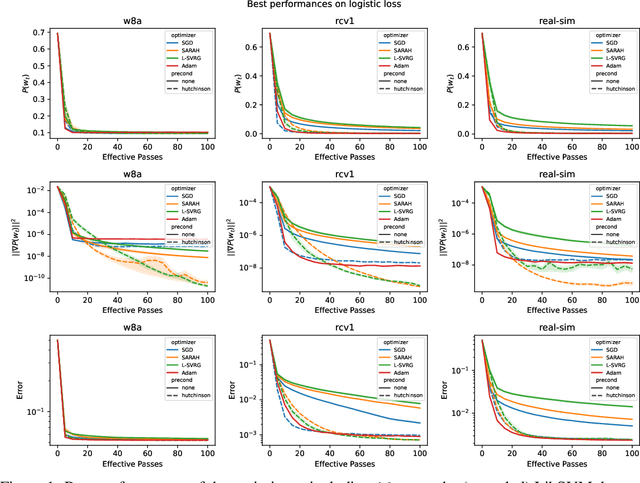
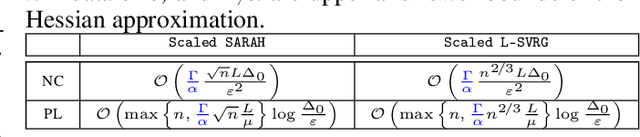
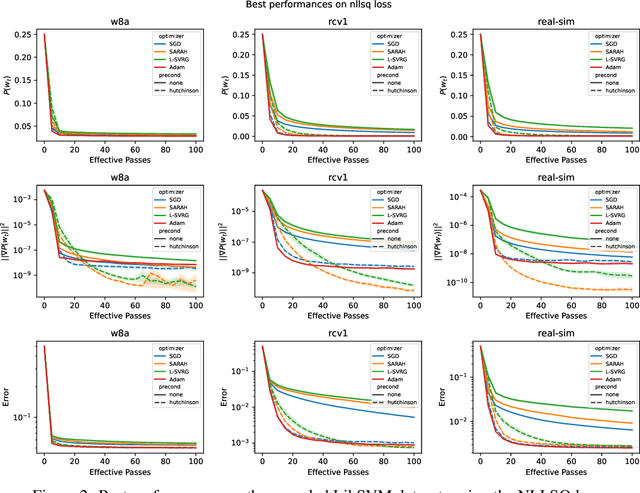
This work considers non-convex finite sum minimization. There are a number of algorithms for such problems, but existing methods often work poorly when the problem is badly scaled and/or ill-conditioned, and a primary goal of this work is to introduce methods that alleviate this issue. Thus, here we include a preconditioner that is based upon Hutchinson's approach to approximating the diagonal of the Hessian, and couple it with several gradient based methods to give new `scaled' algorithms: {\tt Scaled SARAH} and {\tt Scaled L-SVRG}. Theoretical complexity guarantees under smoothness assumptions are presented, and we prove linear convergence when both smoothness and the PL-condition is assumed. Because our adaptively scaled methods use approximate partial second order curvature information, they are better able to mitigate the impact of badly scaled problems, and this improved practical performance is demonstrated in the numerical experiments that are also presented in this work.

Recent Theoretical Advances in Non-Convex Optimization

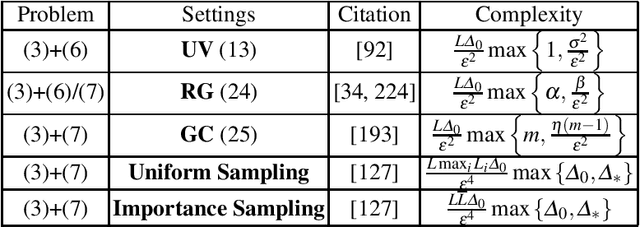
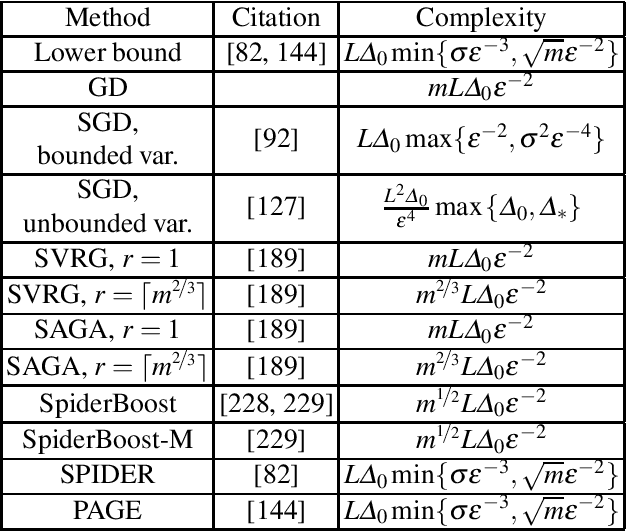
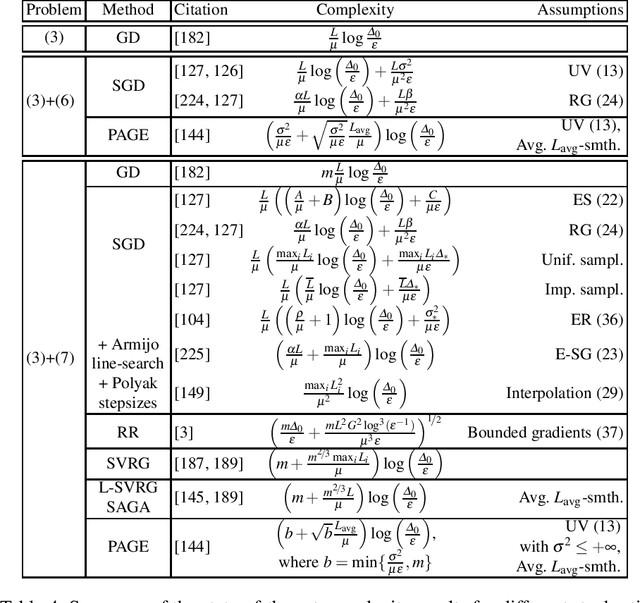
Motivated by recent increased interest in optimization algorithms for non-convex optimization in application to training deep neural networks and other optimization problems in data analysis, we give an overview of recent theoretical results on global performance guarantees of optimization algorithms for non-convex optimization. We start with classical arguments showing that general non-convex problems could not be solved efficiently in a reasonable time. Then we give a list of problems that can be solved efficiently to find the global minimizer by exploiting the structure of the problem as much as it is possible. Another way to deal with non-convexity is to relax the goal from finding the global minimum to finding a stationary point or a local minimum. For this setting, we first present known results for the convergence rates of deterministic first-order methods, which are then followed by a general theoretical analysis of optimal stochastic and randomized gradient schemes, and an overview of the stochastic first-order methods. After that, we discuss quite general classes of non-convex problems, such as minimization of $\alpha$-weakly-quasi-convex functions and functions that satisfy Polyak--Lojasiewicz condition, which still allow obtaining theoretical convergence guarantees of first-order methods. Then we consider higher-order and zeroth-order/derivative-free methods and their convergence rates for non-convex optimization problems.