$ψ$DAG: Projected Stochastic Approximation Iteration for DAG Structure Learning

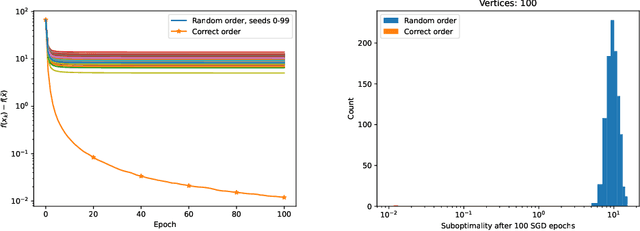
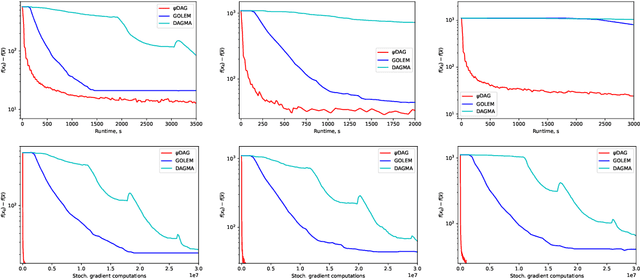
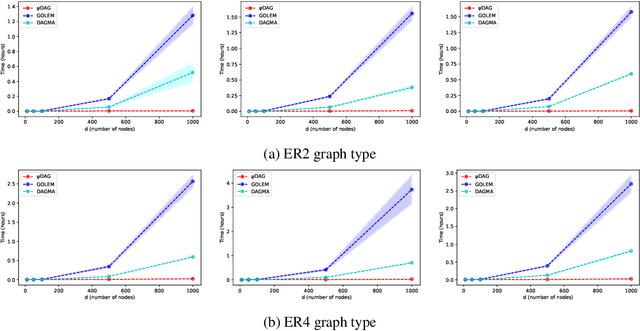
Learning the structure of Directed Acyclic Graphs (DAGs) presents a significant challenge due to the vast combinatorial search space of possible graphs, which scales exponentially with the number of nodes. Recent advancements have redefined this problem as a continuous optimization task by incorporating differentiable acyclicity constraints. These methods commonly rely on algebraic characterizations of DAGs, such as matrix exponentials, to enable the use of gradient-based optimization techniques. Despite these innovations, existing methods often face optimization difficulties due to the highly non-convex nature of DAG constraints and the per-iteration computational complexity. In this work, we present a novel framework for learning DAGs, employing a Stochastic Approximation approach integrated with Stochastic Gradient Descent (SGD)-based optimization techniques. Our framework introduces new projection methods tailored to efficiently enforce DAG constraints, ensuring that the algorithm converges to a feasible local minimum. With its low iteration complexity, the proposed method is well-suited for handling large-scale problems with improved computational efficiency. We demonstrate the effectiveness and scalability of our framework through comprehensive experimental evaluations, which confirm its superior performance across various settings.

Adaptive Optimization Algorithms for Machine Learning

Machine learning assumes a pivotal role in our data-driven world. The increasing scale of models and datasets necessitates quick and reliable algorithms for model training. This dissertation investigates adaptivity in machine learning optimizers. The ensuing chapters are dedicated to various facets of adaptivity, including: 1. personalization and user-specific models via personalized loss, 2. provable post-training model adaptations via meta-learning, 3. learning unknown hyperparameters in real time via hyperparameter variance reduction, 4. fast O(1/k^2) global convergence of second-order methods via stepsized Newton method regardless of the initialization and choice basis, 5. fast and scalable second-order methods via low-dimensional updates. This thesis contributes novel insights, introduces new algorithms with improved convergence guarantees, and improves analyses of popular practical algorithms.

Sketch-and-Project Meets Newton Method: Global $\mathcal O$ Convergence with Low-Rank Updates

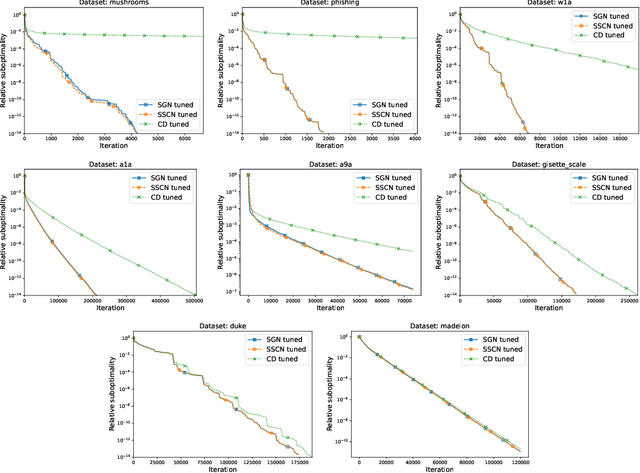
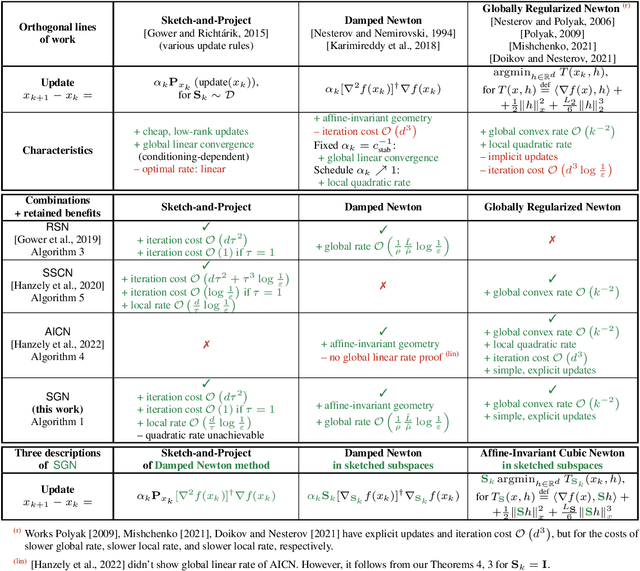
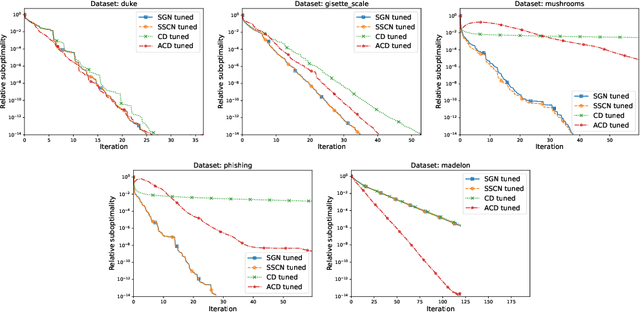
In this paper, we propose the first sketch-and-project Newton method with fast $\mathcal O(k^{-2})$ global convergence rate for self-concordant functions. Our method, SGN, can be viewed in three ways: i) as a sketch-and-project algorithm projecting updates of Newton method, ii) as a cubically regularized Newton ethod in sketched subspaces, and iii) as a damped Newton method in sketched subspaces. SGN inherits best of all three worlds: cheap iteration costs of sketch-and-project methods, state-of-the-art $\mathcal O(k^{-2})$ global convergence rate of full-rank Newton-like methods and the algorithm simplicity of damped Newton methods. Finally, we demonstrate its comparable empirical performance to baseline algorithms.

Convergence of First-Order Algorithms for Meta-Learning with Moreau Envelopes

In this work, we consider the problem of minimizing the sum of Moreau envelopes of given functions, which has previously appeared in the context of meta-learning and personalized federated learning. In contrast to the existing theory that requires running subsolvers until a certain precision is reached, we only assume that a finite number of gradient steps is taken at each iteration. As a special case, our theory allows us to show the convergence of First-Order Model-Agnostic Meta-Learning (FO-MAML) to the vicinity of a solution of Moreau objective. We also study a more general family of first-order algorithms that can be viewed as a generalization of FO-MAML. Our main theoretical achievement is a theoretical improvement upon the inexact SGD framework. In particular, our perturbed-iterate analysis allows for tighter guarantees that improve the dependency on the problem's conditioning. In contrast to the related work on meta-learning, ours does not require any assumptions on the Hessian smoothness, and can leverage smoothness and convexity of the reformulation based on Moreau envelopes. Furthermore, to fill the gaps in the comparison of FO-MAML to the Implicit MAML (iMAML), we show that the objective of iMAML is neither smooth nor convex, implying that it has no convergence guarantees based on the existing theory.

Distributed Newton-Type Methods with Communication Compression and Bernoulli Aggregation

Despite their high computation and communication costs, Newton-type methods remain an appealing option for distributed training due to their robustness against ill-conditioned convex problems. In this work, we study ommunication compression and aggregation mechanisms for curvature information in order to reduce these costs while preserving theoretically superior local convergence guarantees. We prove that the recently developed class of three point compressors (3PC) of Richtarik et al. [2022] for gradient communication can be generalized to Hessian communication as well. This result opens up a wide variety of communication strategies, such as contractive compression} and lazy aggregation, available to our disposal to compress prohibitively costly curvature information. Moreover, we discovered several new 3PC mechanisms, such as adaptive thresholding and Bernoulli aggregation, which require reduced communication and occasional Hessian computations. Furthermore, we extend and analyze our approach to bidirectional communication compression and partial device participation setups to cater to the practical considerations of applications in federated learning. For all our methods, we derive fast condition-number-independent local linear and/or superlinear convergence rates. Finally, with extensive numerical evaluations on convex optimization problems, we illustrate that our designed schemes achieve state-of-the-art communication complexity compared to several key baselines using second-order information.

Lower Bounds and Optimal Algorithms for Personalized Federated Learning

In this work, we consider the optimization formulation of personalized federated learning recently introduced by Hanzely and Richt\'arik (2020) which was shown to give an alternative explanation to the workings of local {\tt SGD} methods. Our first contribution is establishing the first lower bounds for this formulation, for both the communication complexity and the local oracle complexity. Our second contribution is the design of several optimal methods matching these lower bounds in almost all regimes. These are the first provably optimal methods for personalized federated learning. Our optimal methods include an accelerated variant of {\tt FedProx}, and an accelerated variance-reduced version of {\tt FedAvg}/Local {\tt SGD}. We demonstrate the practical superiority of our methods through extensive numerical experiments.