Sketch-and-Project Meets Newton Method: Global $\mathcal O$ Convergence with Low-Rank Updates

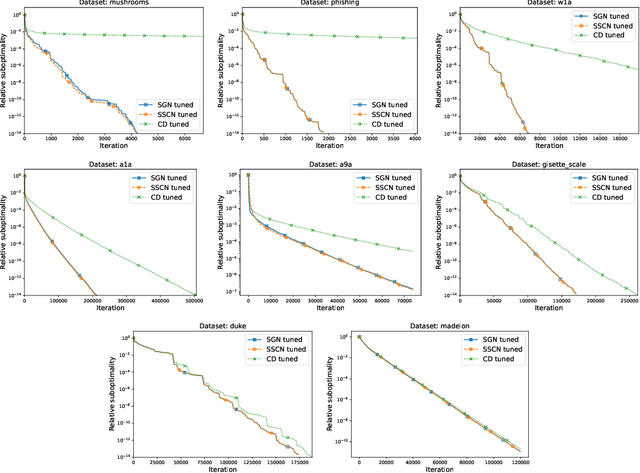
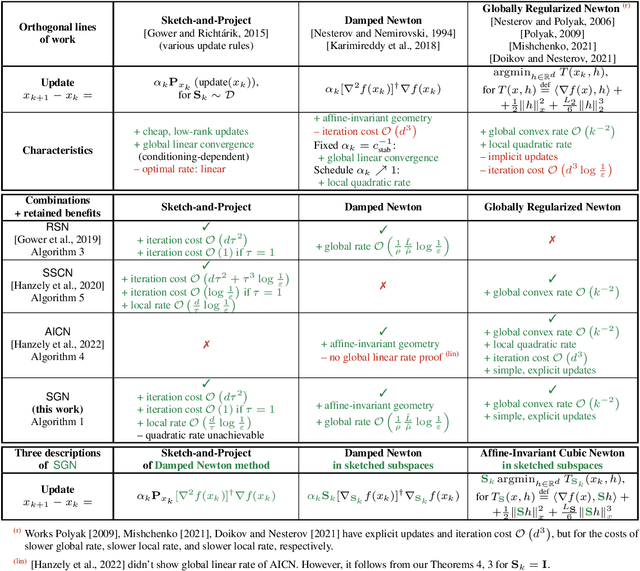
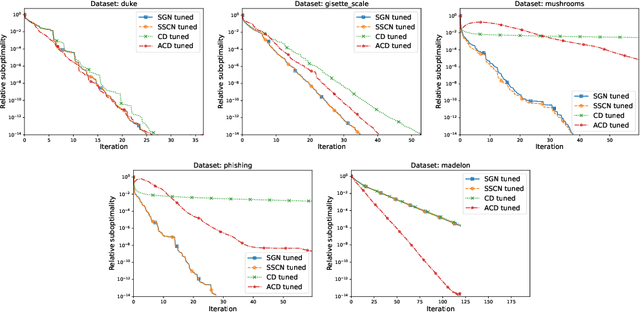
In this paper, we propose the first sketch-and-project Newton method with fast $\mathcal O(k^{-2})$ global convergence rate for self-concordant functions. Our method, SGN, can be viewed in three ways: i) as a sketch-and-project algorithm projecting updates of Newton method, ii) as a cubically regularized Newton ethod in sketched subspaces, and iii) as a damped Newton method in sketched subspaces. SGN inherits best of all three worlds: cheap iteration costs of sketch-and-project methods, state-of-the-art $\mathcal O(k^{-2})$ global convergence rate of full-rank Newton-like methods and the algorithm simplicity of damped Newton methods. Finally, we demonstrate its comparable empirical performance to baseline algorithms.