Smoothing DiLoCo with Primal Averaging for Faster Training of LLMs

We propose Generalized Primal Averaging (GPA), an extension of Nesterov's method in its primal averaging formulation that addresses key limitations of recent averaging-based optimizers such as single-worker DiLoCo and Schedule-Free (SF) in the non-distributed setting. These two recent algorithmic approaches improve the performance of base optimizers, such as AdamW, through different iterate averaging strategies. Schedule-Free explicitly maintains a uniform average of past weights, while single-worker DiLoCo performs implicit averaging by periodically aggregating trajectories, called pseudo-gradients, to update the model parameters. However, single-worker DiLoCo's periodic averaging introduces a two-loop structure, increasing its memory requirements and number of hyperparameters. GPA overcomes these limitations by decoupling the interpolation constant in the primal averaging formulation of Nesterov. This decoupling enables GPA to smoothly average iterates at every step, generalizing and improving upon single-worker DiLoCo. Empirically, GPA consistently outperforms single-worker DiLoCo while removing the two-loop structure, simplifying hyperparameter tuning, and reducing its memory overhead to a single additional buffer. On the Llama-160M model, GPA provides a 24.22% speedup in terms of steps to reach the baseline (AdamW's) validation loss. Likewise, GPA achieves speedups of 12% and 27% on small and large batch setups, respectively, to attain AdamW's validation accuracy on the ImageNet ViT workload. Furthermore, we prove that for any base optimizer with regret bounded by $O(\sqrt{T})$, where $T$ is the number of iterations, GPA can match or exceed the convergence guarantee of the original optimizer, depending on the choice of interpolation constants.

Analysis of an Idealized Stochastic Polyak Method and its Application to Black-Box Model Distillation

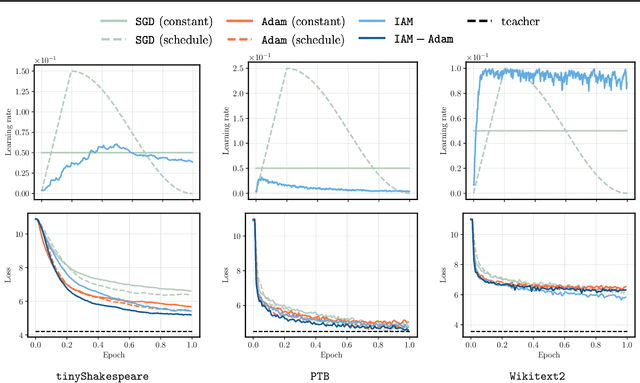
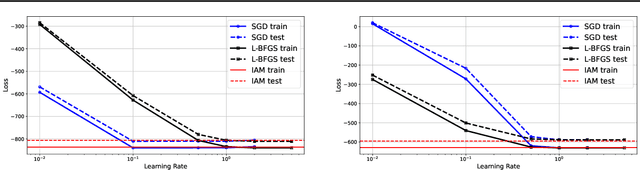
We provide a general convergence theorem of an idealized stochastic Polyak step size called SPS$^*$. Besides convexity, we only assume a local expected gradient bound, that includes locally smooth and locally Lipschitz losses as special cases. We refer to SPS$^*$ as idealized because it requires access to the loss for every training batch evaluated at a solution. It is also ideal, in that it achieves the optimal lower bound for globally Lipschitz function, and is the first Polyak step size to have an $O(1/\sqrt{t})$ anytime convergence in the smooth setting. We show how to combine SPS$^*$ with momentum to achieve the same favorable rates for the last iterate. We conclude with several experiments to validate our theory, and a more practical setting showing how we can distill a teacher GPT-2 model into a smaller student model without any hyperparameter tuning.

Hardware-Aware Parallel Prompt Decoding for Memory-Efficient Acceleration of LLM Inference

The auto-regressive decoding of Large Language Models (LLMs) results in significant overheads in their hardware performance. While recent research has investigated various speculative decoding techniques for multi-token generation, these efforts have primarily focused on improving processing speed such as throughput. Crucially, they often neglect other metrics essential for real-life deployments, such as memory consumption and training cost. To overcome these limitations, we propose a novel parallel prompt decoding that requires only $0.0002$% trainable parameters, enabling efficient training on a single A100-40GB GPU in just 16 hours. Inspired by the human natural language generation process, $PPD$ approximates outputs generated at future timesteps in parallel by using multiple prompt tokens. This approach partially recovers the missing conditional dependency information necessary for multi-token generation, resulting in up to a 28% higher acceptance rate for long-range predictions. Furthermore, we present a hardware-aware dynamic sparse tree technique that adaptively optimizes this decoding scheme to fully leverage the computational capacities on different GPUs. Through extensive experiments across LLMs ranging from MobileLlama to Vicuna-13B on a wide range of benchmarks, our approach demonstrates up to 2.49$\times$ speedup and maintains a minimal runtime memory overhead of just $0.0004$%. More importantly, our parallel prompt decoding can serve as an orthogonal optimization for synergistic integration with existing speculative decoding, showing up to $1.22\times$ further speed improvement. Our code is available at https://github.com/hmarkc/parallel-prompt-decoding.

The Road Less Scheduled

Existing learning rate schedules that do not require specification of the optimization stopping step T are greatly out-performed by learning rate schedules that depend on T. We propose an approach that avoids the need for this stopping time by eschewing the use of schedules entirely, while exhibiting state-of-the-art performance compared to schedules across a wide family of problems ranging from convex problems to large-scale deep learning problems. Our Schedule-Free approach introduces no additional hyper-parameters over standard optimizers with momentum. Our method is a direct consequence of a new theory we develop that unifies scheduling and iterate averaging. An open source implementation of our method is available (https://github.com/facebookresearch/schedule_free).

When, Why and How Much? Adaptive Learning Rate Scheduling by Refinement

Learning rate schedules used in practice bear little resemblance to those recommended by theory. We close much of this theory/practice gap, and as a consequence are able to derive new problem-adaptive learning rate schedules. Our key technical contribution is a refined analysis of learning rate schedules for a wide class of optimization algorithms (including SGD). In contrast to most prior works that study the convergence of the average iterate, we study the last iterate, which is what most people use in practice. When considering only worst-case analysis, our theory predicts that the best choice is the linear decay schedule: a popular choice in practice that sets the stepsize proportionally to $1 - t/T$, where $t$ is the current iteration and $T$ is the total number of steps. To go beyond this worst-case analysis, we use the observed gradient norms to derive schedules refined for any particular task. These refined schedules exhibit learning rate warm-up and rapid learning rate annealing near the end of training. Ours is the first systematic approach to automatically yield both of these properties. We perform the most comprehensive evaluation of learning rate schedules to date, evaluating across 10 diverse deep learning problems, a series of LLMs, and a suite of logistic regression problems. We validate that overall, the linear-decay schedule matches or outperforms all commonly used default schedules including cosine annealing, and that our schedule refinement method gives further improvements.

Adaptive Proximal Gradient Method for Convex Optimization

In this paper, we explore two fundamental first-order algorithms in convex optimization, namely, gradient descent (GD) and proximal gradient method (ProxGD). Our focus is on making these algorithms entirely adaptive by leveraging local curvature information of smooth functions. We propose adaptive versions of GD and ProxGD that are based on observed gradient differences and, thus, have no added computational costs. Moreover, we prove convergence of our methods assuming only local Lipschitzness of the gradient. In addition, the proposed versions allow for even larger stepsizes than those initially suggested in [MM20].

Prodigy: An Expeditiously Adaptive Parameter-Free Learner

We consider the problem of estimating the learning rate in adaptive methods, such as Adagrad and Adam. We describe two techniques, Prodigy and Resetting, to provably estimate the distance to the solution $D$, which is needed to set the learning rate optimally. Our techniques are modifications of the D-Adaptation method for learning-rate-free learning. Our methods improve upon the convergence rate of D-Adaptation by a factor of $O(\sqrt{\log(D/d_0)})$, where $d_0$ is the initial estimate of $D$. We test our methods on 12 common logistic-regression benchmark datasets, VGG11 and ResNet-50 training on CIFAR10, ViT training on Imagenet, LSTM training on IWSLT14, DLRM training on Criteo dataset, VarNet on Knee MRI dataset, as well as RoBERTa and GPT transformer training on BookWiki. Our experimental results show that our approaches consistently outperform D-Adaptation and reach test accuracy values close to that of hand-tuned Adam.

Partially Personalized Federated Learning: Breaking the Curse of Data Heterogeneity

We present a partially personalized formulation of Federated Learning (FL) that strikes a balance between the flexibility of personalization and cooperativeness of global training. In our framework, we split the variables into global parameters, which are shared across all clients, and individual local parameters, which are kept private. We prove that under the right split of parameters, it is possible to find global parameters that allow each client to fit their data perfectly, and refer to the obtained problem as overpersonalized. For instance, the shared global parameters can be used to learn good data representations, whereas the personalized layers are fine-tuned for a specific client. Moreover, we present a simple algorithm for the partially personalized formulation that offers significant benefits to all clients. In particular, it breaks the curse of data heterogeneity in several settings, such as training with local steps, asynchronous training, and Byzantine-robust training.

DoWG Unleashed: An Efficient Universal Parameter-Free Gradient Descent Method

This paper proposes a new easy-to-implement parameter-free gradient-based optimizer: DoWG (Distance over Weighted Gradients). We prove that DoWG is efficient -- matching the convergence rate of optimally tuned gradient descent in convex optimization up to a logarithmic factor without tuning any parameters, and universal -- automatically adapting to both smooth and nonsmooth problems. While popular algorithms such as AdaGrad, Adam, or DoG compute a running average of the squared gradients, DoWG maintains a new distance-based weighted version of the running average, which is crucial to achieve the desired properties. To our best knowledge, DoWG is the first parameter-free, efficient, and universal algorithm that does not require backtracking search procedures. It is also the first parameter-free AdaGrad style algorithm that adapts to smooth optimization. To complement our theory, we also show empirically that DoWG trains at the edge of stability, and validate its effectiveness on practical machine learning tasks. This paper further uncovers the underlying principle behind the success of the AdaGrad family of algorithms by presenting a novel analysis of Normalized Gradient Descent (NGD), that shows NGD adapts to smoothness when it exists, with no change to the stepsize. This establishes the universality of NGD and partially explains the empirical observation that it trains at the edge of stability in a much more general setup compared to standard gradient descent. The latter might be of independent interest to the community.

Two Losses Are Better Than One: Faster Optimization Using a Cheaper Proxy

We present an algorithm for minimizing an objective with hard-to-compute gradients by using a related, easier-to-access function as a proxy. Our algorithm is based on approximate proximal point iterations on the proxy combined with relatively few stochastic gradients from the objective. When the difference between the objective and the proxy is $\delta$-smooth, our algorithm guarantees convergence at a rate matching stochastic gradient descent on a $\delta$-smooth objective, which can lead to substantially better sample efficiency. Our algorithm has many potential applications in machine learning, and provides a principled means of leveraging synthetic data, physics simulators, mixed public and private data, and more.