Adaptive Proximal Gradient Method for Convex Optimization

In this paper, we explore two fundamental first-order algorithms in convex optimization, namely, gradient descent (GD) and proximal gradient method (ProxGD). Our focus is on making these algorithms entirely adaptive by leveraging local curvature information of smooth functions. We propose adaptive versions of GD and ProxGD that are based on observed gradient differences and, thus, have no added computational costs. Moreover, we prove convergence of our methods assuming only local Lipschitzness of the gradient. In addition, the proposed versions allow for even larger stepsizes than those initially suggested in [MM20].

Beyond the Golden Ratio for Variational Inequality Algorithms

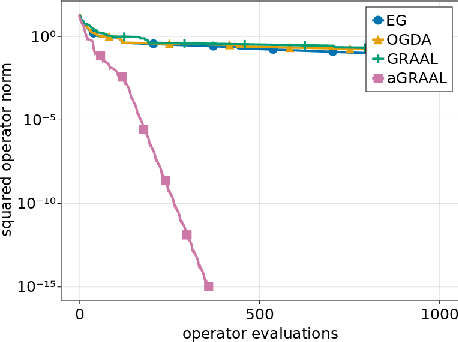
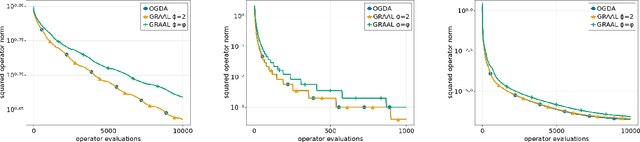
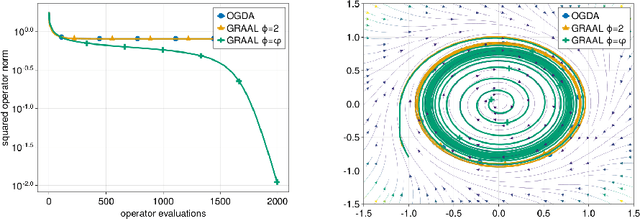
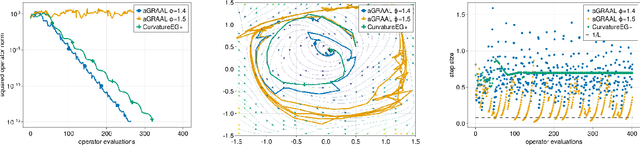
We improve the understanding of the $\textit{golden ratio algorithm}$, which solves monotone variational inequalities (VI) and convex-concave min-max problems via the distinctive feature of adapting the step sizes to the local Lipschitz constants. Adaptive step sizes not only eliminate the need to pick hyperparameters, but they also remove the necessity of global Lipschitz continuity and can increase from one iteration to the next. We first establish the equivalence of this algorithm with popular VI methods such as reflected gradient, Popov or optimistic gradient descent-ascent in the unconstrained case with constant step sizes. We then move on to the constrained setting and introduce a new analysis that allows to use larger step sizes, to complete the bridge between the golden ratio algorithm and the existing algorithms in the literature. Doing so, we actually eliminate the link between the golden ratio $\frac{1+\sqrt{5}}{2}$ and the algorithm. Moreover, we improve the adaptive version of the algorithm, first by removing the maximum step size hyperparameter (an artifact from the analysis) to improve the complexity bound, and second by adjusting it to nonmonotone problems with weak Minty solutions, with superior empirical performance.

Over-the-Air Computation for Distributed Systems: Something Old and Something New

Facing the upcoming era of Internet-of-Things and connected intelligence, efficient information processing, computation and communication design becomes a key challenge in large-scale intelligent systems. Recently, Over-the-Air (OtA) computation has been proposed for data aggregation and distributed function computation over a large set of network nodes. Theoretical foundations for this concept exist for a long time, but it was mainly investigated within the context of wireless sensor networks. There are still many open questions when applying OtA computation in different types of distributed systems where modern wireless communication technology is applied. In this article, we provide a comprehensive overview of the OtA computation principle and its applications in distributed learning, control, and inference systems, for both server-coordinated and fully decentralized architectures. Particularly, we highlight the importance of the statistical heterogeneity of data and wireless channels, the temporal evolution of model updates, and the choice of performance metrics, for the communication design in OtA federated learning (FL) systems. Several key challenges in privacy, security and robustness aspects of OtA FL are also identified for further investigation.

Over-the-Air Computation with Multiple Receivers: A Space-Time Approach

Over-the-air (OtA) computation is a newly emerged concept for achieving resource-efficient data aggregation over a large number of wireless nodes. Current research on this topic only considers the standard star topology with multiple senders transmitting information to one receiver. In this work, we investigate how to achieve OtA computation with multiple receivers, and we propose a novel communication design by exploiting joint precoding and decoding over multiple time slots. The optimal precoding and decoding vectors are determined by solving an optimization problem that aims at minimizing the mean squared error of aggregated data under the unbiasedness condition and the power constraints. We show that with our proposed multi-slot design, we can save communication resources (e.g., time slots) and achieve smaller estimation error as compared to the baseline approach of separating different receivers over time.

A first-order primal-dual method with adaptivity to local smoothness

We consider the problem of finding a saddle point for the convex-concave objective $\min_x \max_y f(x) + \langle Ax, y\rangle - g^*(y)$, where $f$ is a convex function with locally Lipschitz gradient and $g$ is convex and possibly non-smooth. We propose an adaptive version of the Condat-V\~u algorithm, which alternates between primal gradient steps and dual proximal steps. The method achieves stepsize adaptivity through a simple rule involving $\|A\|$ and the norm of recently computed gradients of $f$. Under standard assumptions, we prove an $\mathcal{O}(k^{-1})$ ergodic convergence rate. Furthermore, when $f$ is also locally strongly convex and $A$ has full row rank we show that our method converges with a linear rate. Numerical experiments are provided for illustrating the practical performance of the algorithm.

Stochastic Variance Reduction for Variational Inequality Methods

We propose stochastic variance reduced algorithms for solving convex-concave saddle point problems, monotone variational inequalities, and monotone inclusions. Our framework applies to extragradient, forward-backward-forward, and forward-reflected-backward methods both in Euclidean and Bregman setups. All proposed methods converge in exactly the same setting as their deterministic counterparts and they either match or improve the best-known complexities for solving structured min-max problems. Our results reinforce the correspondence between variance reduction in variational inequalities and minimization. We also illustrate the improvements of our approach with numerical evaluations on matrix games.

Convergence of adaptive algorithms for weakly convex constrained optimization

We analyze the adaptive first order algorithm AMSGrad, for solving a constrained stochastic optimization problem with a weakly convex objective. We prove the $\mathcal{\tilde O}(t^{-1/4})$ rate of convergence for the norm of the gradient of Moreau envelope, which is the standard stationarity measure for this class of problems. It matches the known rates that adaptive algorithms enjoy for the specific case of unconstrained smooth stochastic optimization. Our analysis works with mini-batch size of $1$, constant first and second order moment parameters, and possibly unbounded optimization domains. Finally, we illustrate the applications and extensions of our results to specific problems and algorithms.

A new regret analysis for Adam-type algorithms

In this paper, we focus on a theory-practice gap for Adam and its variants (AMSgrad, AdamNC, etc.). In practice, these algorithms are used with a constant first-order moment parameter $\beta_{1}$ (typically between $0.9$ and $0.99$). In theory, regret guarantees for online convex optimization require a rapidly decaying $\beta_{1}\to0$ schedule. We show that this is an artifact of the standard analysis and propose a novel framework that allows us to derive optimal, data-dependent regret bounds with a constant $\beta_{1}$, without further assumptions. We also demonstrate the flexibility of our analysis on a wide range of different algorithms and settings.

Adaptive gradient descent without descent

We present a strikingly simple proof that two rules are sufficient to automate gradient descent: 1) don't increase the stepsize too fast and 2) don't overstep the local curvature. No need for functional values, no line search, no information about the function except for the gradients. By following these rules, you get a method adaptive to the local geometry, with convergence guarantees depending only on smoothness in a neighborhood of a solution. Given that the problem is convex, our method will converge even if the global smoothness constant is infinity. As an illustration, it can minimize arbitrary continuously twice-differentiable convex function. We examine its performance on a range of convex and nonconvex problems, including matrix factorization and training of ResNet-18.

Revisiting Stochastic Extragradient

We consider a new extension of the extragradient method that is motivated by approximating implicit updates. Since in a recent work~\cite{chavdarova2019reducing} it was shown that the existing stochastic extragradient algorithm (called mirror-prox) of~\cite{juditsky2011solving} diverges on a simple bilinear problem, we prove guarantees for solving variational inequality that are more general than in~\cite{juditsky2011solving}. Furthermore, we illustrate numerically that the proposed variant converges faster than many other methods on the example of~\cite{chavdarova2019reducing}. We also discuss how extragradient can be applied to training Generative Adversarial Networks (GANs). Our experiments on GANs demonstrate that the introduced approach may make the training faster in terms of data passes, while its higher iteration complexity makes the advantage smaller. To further accelerate method's convergence on problems such as bilinear minimax, we combine the extragradient step with negative momentum~\cite{gidel2018negative} and discuss the optimal momentum value.