Learning-Rate-Free Learning by D-Adaptation
Paper and Code
Jan 20, 2023
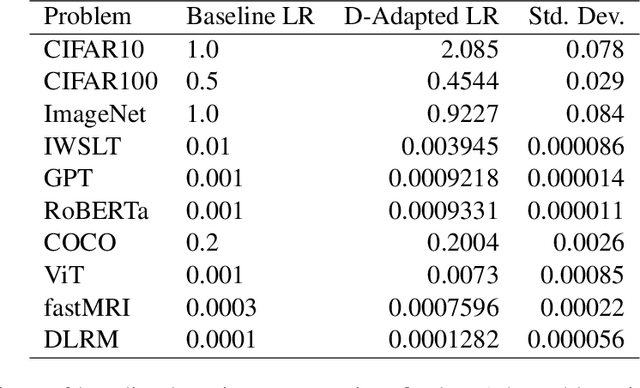


The speed of gradient descent for convex Lipschitz functions is highly dependent on the choice of learning rate. Setting the learning rate to achieve the optimal convergence rate requires knowing the distance D from the initial point to the solution set. In this work, we describe a single-loop method, with no back-tracking or line searches, which does not require knowledge of $D$ yet asymptotically achieves the optimal rate of convergence for the complexity class of convex Lipschitz functions. Our approach is the first parameter-free method for this class without additional multiplicative log factors in the convergence rate. We present extensive experiments for SGD and Adam variants of our method, where the method automatically matches hand-tuned learning rates across more than a dozen diverse machine learning problems, including large-scale vision and language problems. Our method is practical, efficient and requires no additional function value or gradient evaluations each step. An open-source implementation is available (https://github.com/facebookresearch/dadaptation).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge