Analysis of an Idealized Stochastic Polyak Method and its Application to Black-Box Model Distillation

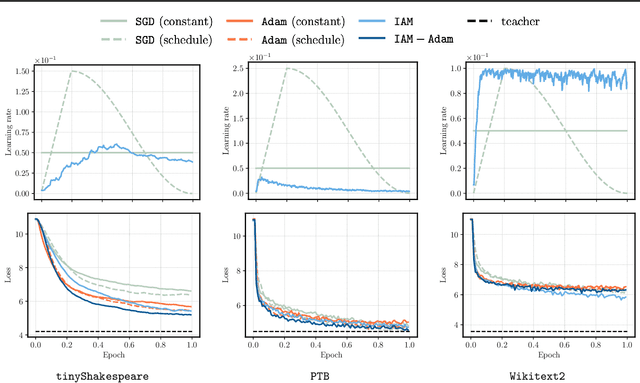
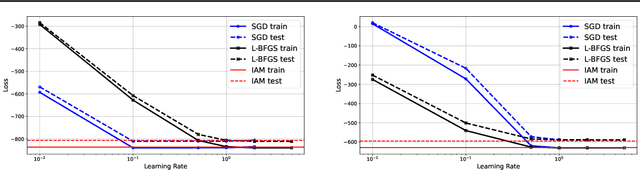
We provide a general convergence theorem of an idealized stochastic Polyak step size called SPS$^*$. Besides convexity, we only assume a local expected gradient bound, that includes locally smooth and locally Lipschitz losses as special cases. We refer to SPS$^*$ as idealized because it requires access to the loss for every training batch evaluated at a solution. It is also ideal, in that it achieves the optimal lower bound for globally Lipschitz function, and is the first Polyak step size to have an $O(1/\sqrt{t})$ anytime convergence in the smooth setting. We show how to combine SPS$^*$ with momentum to achieve the same favorable rates for the last iterate. We conclude with several experiments to validate our theory, and a more practical setting showing how we can distill a teacher GPT-2 model into a smaller student model without any hyperparameter tuning.

Sharpness-Aware Minimization: General Analysis and Improved Rates

Sharpness-Aware Minimization (SAM) has emerged as a powerful method for improving generalization in machine learning models by minimizing the sharpness of the loss landscape. However, despite its success, several important questions regarding the convergence properties of SAM in non-convex settings are still open, including the benefits of using normalization in the update rule, the dependence of the analysis on the restrictive bounded variance assumption, and the convergence guarantees under different sampling strategies. To address these questions, in this paper, we provide a unified analysis of SAM and its unnormalized variant (USAM) under one single flexible update rule (Unified SAM), and we present convergence results of the new algorithm under a relaxed and more natural assumption on the stochastic noise. Our analysis provides convergence guarantees for SAM under different step size selections for non-convex problems and functions that satisfy the Polyak-Lojasiewicz (PL) condition (a non-convex generalization of strongly convex functions). The proposed theory holds under the arbitrary sampling paradigm, which includes importance sampling as special case, allowing us to analyze variants of SAM that were never explicitly considered in the literature. Experiments validate the theoretical findings and further demonstrate the practical effectiveness of Unified SAM in training deep neural networks for image classification tasks.

Stochastic Polyak Step-sizes and Momentum: Convergence Guarantees and Practical Performance

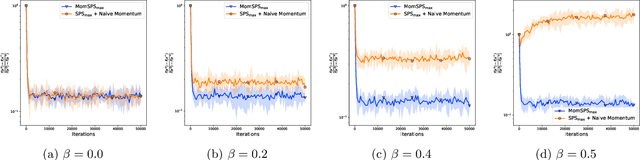
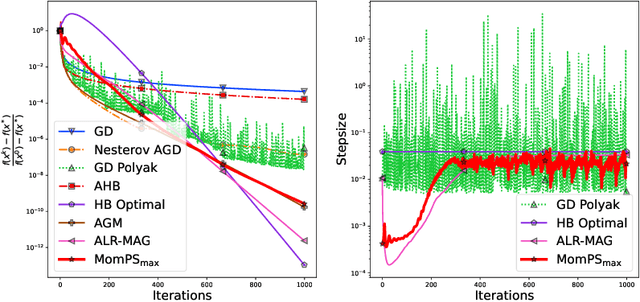
Stochastic gradient descent with momentum, also known as Stochastic Heavy Ball method (SHB), is one of the most popular algorithms for solving large-scale stochastic optimization problems in various machine learning tasks. In practical scenarios, tuning the step-size and momentum parameters of the method is a prohibitively expensive and time-consuming process. In this work, inspired by the recent advantages of stochastic Polyak step-size in the performance of stochastic gradient descent (SGD), we propose and explore new Polyak-type variants suitable for the update rule of the SHB method. In particular, using the Iterate Moving Average (IMA) viewpoint of SHB, we propose and analyze three novel step-size selections: MomSPS$_{\max}$, MomDecSPS, and MomAdaSPS. For MomSPS$_{\max}$, we provide convergence guarantees for SHB to a neighborhood of the solution for convex and smooth problems (without assuming interpolation). If interpolation is also satisfied, then using MomSPS$_{\max}$, SHB converges to the true solution at a fast rate matching the deterministic HB. The other two variants, MomDecSPS and MomAdaSPS, are the first adaptive step-sizes for SHB that guarantee convergence to the exact minimizer without prior knowledge of the problem parameters and without assuming interpolation. The convergence analysis of SHB is tight and obtains the convergence guarantees of SGD with stochastic Polyak step-sizes as a special case. We supplement our analysis with experiments that validate the theory and demonstrate the effectiveness and robustness of the new algorithms.