Analysis of an Idealized Stochastic Polyak Method and its Application to Black-Box Model Distillation

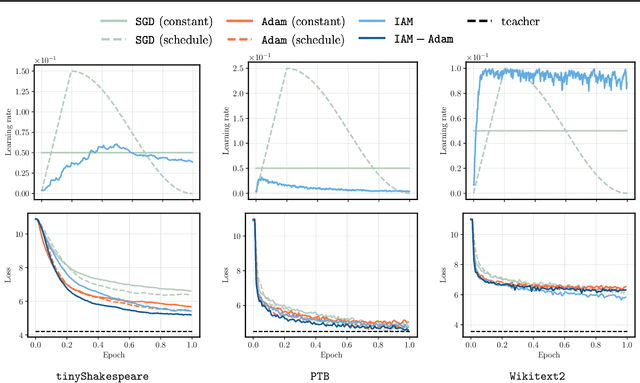
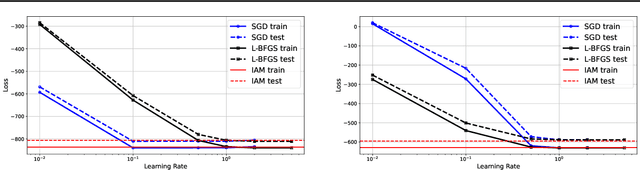
We provide a general convergence theorem of an idealized stochastic Polyak step size called SPS$^*$. Besides convexity, we only assume a local expected gradient bound, that includes locally smooth and locally Lipschitz losses as special cases. We refer to SPS$^*$ as idealized because it requires access to the loss for every training batch evaluated at a solution. It is also ideal, in that it achieves the optimal lower bound for globally Lipschitz function, and is the first Polyak step size to have an $O(1/\sqrt{t})$ anytime convergence in the smooth setting. We show how to combine SPS$^*$ with momentum to achieve the same favorable rates for the last iterate. We conclude with several experiments to validate our theory, and a more practical setting showing how we can distill a teacher GPT-2 model into a smaller student model without any hyperparameter tuning.

Sharpness-Aware Minimization: General Analysis and Improved Rates

Sharpness-Aware Minimization (SAM) has emerged as a powerful method for improving generalization in machine learning models by minimizing the sharpness of the loss landscape. However, despite its success, several important questions regarding the convergence properties of SAM in non-convex settings are still open, including the benefits of using normalization in the update rule, the dependence of the analysis on the restrictive bounded variance assumption, and the convergence guarantees under different sampling strategies. To address these questions, in this paper, we provide a unified analysis of SAM and its unnormalized variant (USAM) under one single flexible update rule (Unified SAM), and we present convergence results of the new algorithm under a relaxed and more natural assumption on the stochastic noise. Our analysis provides convergence guarantees for SAM under different step size selections for non-convex problems and functions that satisfy the Polyak-Lojasiewicz (PL) condition (a non-convex generalization of strongly convex functions). The proposed theory holds under the arbitrary sampling paradigm, which includes importance sampling as special case, allowing us to analyze variants of SAM that were never explicitly considered in the literature. Experiments validate the theoretical findings and further demonstrate the practical effectiveness of Unified SAM in training deep neural networks for image classification tasks.

Multiplayer Federated Learning: Reaching Equilibrium with Less Communication

Traditional Federated Learning (FL) approaches assume collaborative clients with aligned objectives working towards a shared global model. However, in many real-world scenarios, clients act as rational players with individual objectives and strategic behaviors, a concept that existing FL frameworks are not equipped to adequately address. To bridge this gap, we introduce Multiplayer Federated Learning (MpFL), a novel framework that models the clients in the FL environment as players in a game-theoretic context, aiming to reach an equilibrium. In this scenario, each player tries to optimize their own utility function, which may not align with the collective goal. Within MpFL, we propose Per-Player Local Stochastic Gradient Descent (PEARL-SGD), an algorithm in which each player/client performs local updates independently and periodically communicates with other players. We theoretically analyze PEARL-SGD and prove that it reaches a neighborhood of equilibrium with less communication in the stochastic setup compared to its non-local counterpart. Finally, we verify our theoretical findings through numerical experiments.

Stochastic Polyak Step-sizes and Momentum: Convergence Guarantees and Practical Performance

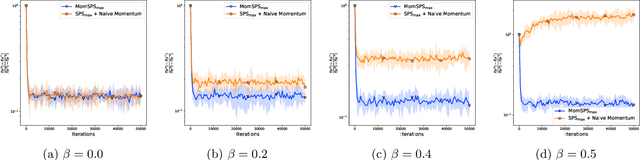
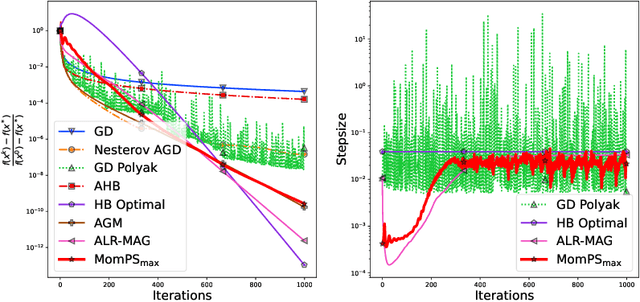
Stochastic gradient descent with momentum, also known as Stochastic Heavy Ball method (SHB), is one of the most popular algorithms for solving large-scale stochastic optimization problems in various machine learning tasks. In practical scenarios, tuning the step-size and momentum parameters of the method is a prohibitively expensive and time-consuming process. In this work, inspired by the recent advantages of stochastic Polyak step-size in the performance of stochastic gradient descent (SGD), we propose and explore new Polyak-type variants suitable for the update rule of the SHB method. In particular, using the Iterate Moving Average (IMA) viewpoint of SHB, we propose and analyze three novel step-size selections: MomSPS$_{\max}$, MomDecSPS, and MomAdaSPS. For MomSPS$_{\max}$, we provide convergence guarantees for SHB to a neighborhood of the solution for convex and smooth problems (without assuming interpolation). If interpolation is also satisfied, then using MomSPS$_{\max}$, SHB converges to the true solution at a fast rate matching the deterministic HB. The other two variants, MomDecSPS and MomAdaSPS, are the first adaptive step-sizes for SHB that guarantee convergence to the exact minimizer without prior knowledge of the problem parameters and without assuming interpolation. The convergence analysis of SHB is tight and obtains the convergence guarantees of SGD with stochastic Polyak step-sizes as a special case. We supplement our analysis with experiments that validate the theory and demonstrate the effectiveness and robustness of the new algorithms.

Dissipative Gradient Descent Ascent Method: A Control Theory Inspired Algorithm for Min-max Optimization

Gradient Descent Ascent (GDA) methods for min-max optimization problems typically produce oscillatory behavior that can lead to instability, e.g., in bilinear settings. To address this problem, we introduce a dissipation term into the GDA updates to dampen these oscillations. The proposed Dissipative GDA (DGDA) method can be seen as performing standard GDA on a state-augmented and regularized saddle function that does not strictly introduce additional convexity/concavity. We theoretically show the linear convergence of DGDA in the bilinear and strongly convex-strongly concave settings and assess its performance by comparing DGDA with other methods such as GDA, Extra-Gradient (EG), and Optimistic GDA. Our findings demonstrate that DGDA surpasses these methods, achieving superior convergence rates. We support our claims with two numerical examples that showcase DGDA's effectiveness in solving saddle point problems.

Stochastic Extragradient with Random Reshuffling: Improved Convergence for Variational Inequalities

The Stochastic Extragradient (SEG) method is one of the most popular algorithms for solving finite-sum min-max optimization and variational inequality problems (VIPs) appearing in various machine learning tasks. However, existing convergence analyses of SEG focus on its with-replacement variants, while practical implementations of the method randomly reshuffle components and sequentially use them. Unlike the well-studied with-replacement variants, SEG with Random Reshuffling (SEG-RR) lacks established theoretical guarantees. In this work, we provide a convergence analysis of SEG-RR for three classes of VIPs: (i) strongly monotone, (ii) affine, and (iii) monotone. We derive conditions under which SEG-RR achieves a faster convergence rate than the uniform with-replacement sampling SEG. In the monotone setting, our analysis of SEG-RR guarantees convergence to an arbitrary accuracy without large batch sizes, a strong requirement needed in the classical with-replacement SEG. As a byproduct of our results, we provide convergence guarantees for Shuffle Once SEG (shuffles the data only at the beginning of the algorithm) and the Incremental Extragradient (does not shuffle the data). We supplement our analysis with experiments validating empirically the superior performance of SEG-RR over the classical with-replacement sampling SEG.

Remove that Square Root: A New Efficient Scale-Invariant Version of AdaGrad

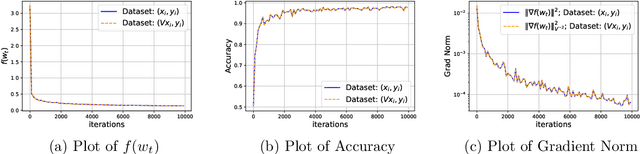
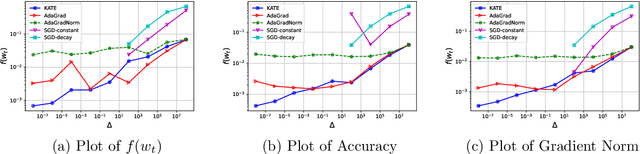
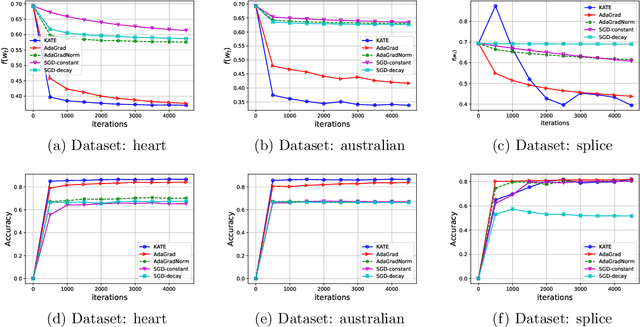
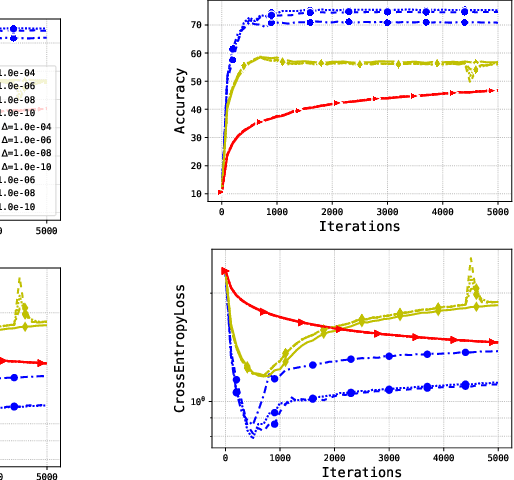
Adaptive methods are extremely popular in machine learning as they make learning rate tuning less expensive. This paper introduces a novel optimization algorithm named KATE, which presents a scale-invariant adaptation of the well-known AdaGrad algorithm. We prove the scale-invariance of KATE for the case of Generalized Linear Models. Moreover, for general smooth non-convex problems, we establish a convergence rate of $O \left(\frac{\log T}{\sqrt{T}} \right)$ for KATE, matching the best-known ones for AdaGrad and Adam. We also compare KATE to other state-of-the-art adaptive algorithms Adam and AdaGrad in numerical experiments with different problems, including complex machine learning tasks like image classification and text classification on real data. The results indicate that KATE consistently outperforms AdaGrad and matches/surpasses the performance of Adam in all considered scenarios.

Locally Adaptive Federated Learning via Stochastic Polyak Stepsizes

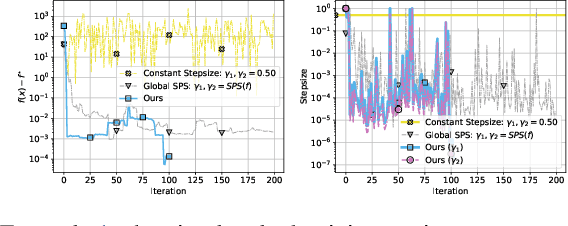
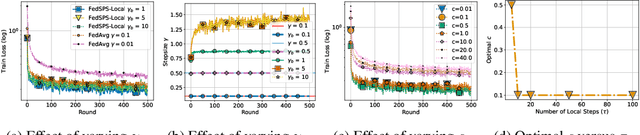
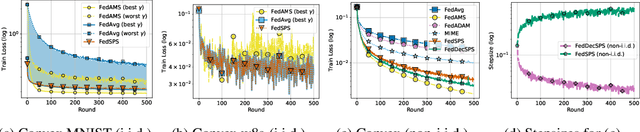
State-of-the-art federated learning algorithms such as FedAvg require carefully tuned stepsizes to achieve their best performance. The improvements proposed by existing adaptive federated methods involve tuning of additional hyperparameters such as momentum parameters, and consider adaptivity only in the server aggregation round, but not locally. These methods can be inefficient in many practical scenarios because they require excessive tuning of hyperparameters and do not capture local geometric information. In this work, we extend the recently proposed stochastic Polyak stepsize (SPS) to the federated learning setting, and propose new locally adaptive and nearly parameter-free distributed SPS variants (FedSPS and FedDecSPS). We prove that FedSPS converges linearly in strongly convex and sublinearly in convex settings when the interpolation condition (overparametrization) is satisfied, and converges to a neighborhood of the solution in the general case. We extend our proposed method to a decreasing stepsize version FedDecSPS, that converges also when the interpolation condition does not hold. We validate our theoretical claims by performing illustrative convex experiments. Our proposed algorithms match the optimization performance of FedAvg with the best tuned hyperparameters in the i.i.d. case, and outperform FedAvg in the non-i.i.d. case.

Communication-Efficient Gradient Descent-Accent Methods for Distributed Variational Inequalities: Unified Analysis and Local Updates

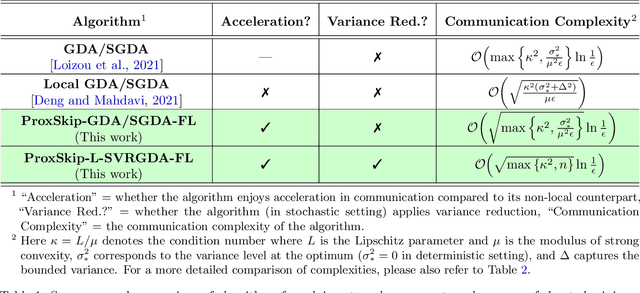
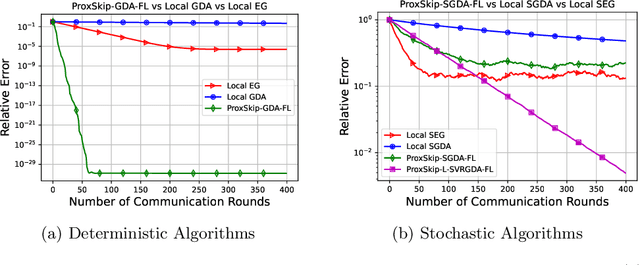
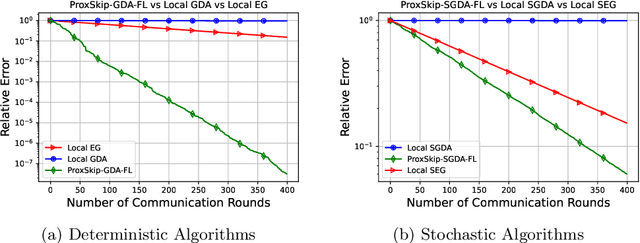
Distributed and federated learning algorithms and techniques associated primarily with minimization problems. However, with the increase of minimax optimization and variational inequality problems in machine learning, the necessity of designing efficient distributed/federated learning approaches for these problems is becoming more apparent. In this paper, we provide a unified convergence analysis of communication-efficient local training methods for distributed variational inequality problems (VIPs). Our approach is based on a general key assumption on the stochastic estimates that allows us to propose and analyze several novel local training algorithms under a single framework for solving a class of structured non-monotone VIPs. We present the first local gradient descent-accent algorithms with provable improved communication complexity for solving distributed variational inequalities on heterogeneous data. The general algorithmic framework recovers state-of-the-art algorithms and their sharp convergence guarantees when the setting is specialized to minimization or minimax optimization problems. Finally, we demonstrate the strong performance of the proposed algorithms compared to state-of-the-art methods when solving federated minimax optimization problems.

Single-Call Stochastic Extragradient Methods for Structured Non-monotone Variational Inequalities: Improved Analysis under Weaker Conditions

Single-call stochastic extragradient methods, like stochastic past extragradient (SPEG) and stochastic optimistic gradient (SOG), have gained a lot of interest in recent years and are one of the most efficient algorithms for solving large-scale min-max optimization and variational inequalities problems (VIP) appearing in various machine learning tasks. However, despite their undoubted popularity, current convergence analyses of SPEG and SOG require a bounded variance assumption. In addition, several important questions regarding the convergence properties of these methods are still open, including mini-batching, efficient step-size selection, and convergence guarantees under different sampling strategies. In this work, we address these questions and provide convergence guarantees for two large classes of structured non-monotone VIPs: (i) quasi-strongly monotone problems (a generalization of strongly monotone problems) and (ii) weak Minty variational inequalities (a generalization of monotone and Minty VIPs). We introduce the expected residual condition, explain its benefits, and show how it can be used to obtain a strictly weaker bound than previously used growth conditions, expected co-coercivity, or bounded variance assumptions. Equipped with this condition, we provide theoretical guarantees for the convergence of single-call extragradient methods for different step-size selections, including constant, decreasing, and step-size-switching rules. Furthermore, our convergence analysis holds under the arbitrary sampling paradigm, which includes importance sampling and various mini-batching strategies as special cases.