Multiplayer Federated Learning: Reaching Equilibrium with Less Communication

Traditional Federated Learning (FL) approaches assume collaborative clients with aligned objectives working towards a shared global model. However, in many real-world scenarios, clients act as rational players with individual objectives and strategic behaviors, a concept that existing FL frameworks are not equipped to adequately address. To bridge this gap, we introduce Multiplayer Federated Learning (MpFL), a novel framework that models the clients in the FL environment as players in a game-theoretic context, aiming to reach an equilibrium. In this scenario, each player tries to optimize their own utility function, which may not align with the collective goal. Within MpFL, we propose Per-Player Local Stochastic Gradient Descent (PEARL-SGD), an algorithm in which each player/client performs local updates independently and periodically communicates with other players. We theoretically analyze PEARL-SGD and prove that it reaches a neighborhood of equilibrium with less communication in the stochastic setup compared to its non-local counterpart. Finally, we verify our theoretical findings through numerical experiments.

Censored Sampling of Diffusion Models Using 3 Minutes of Human Feedback

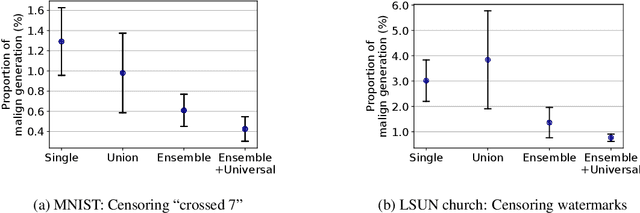
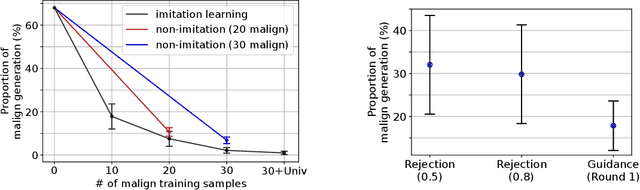
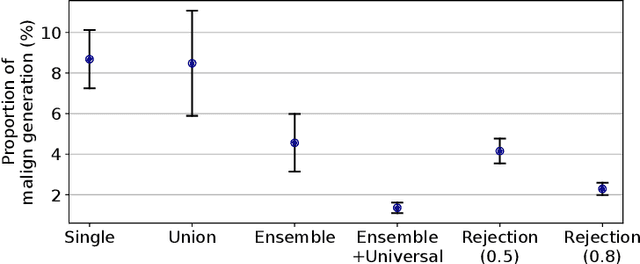
Diffusion models have recently shown remarkable success in high-quality image generation. Sometimes, however, a pre-trained diffusion model exhibits partial misalignment in the sense that the model can generate good images, but it sometimes outputs undesirable images. If so, we simply need to prevent the generation of the bad images, and we call this task censoring. In this work, we present censored generation with a pre-trained diffusion model using a reward model trained on minimal human feedback. We show that censoring can be accomplished with extreme human feedback efficiency and that labels generated with a mere few minutes of human feedback are sufficient. Code available at: https://github.com/tetrzim/diffusion-human-feedback.

Robust Probabilistic Time Series Forecasting

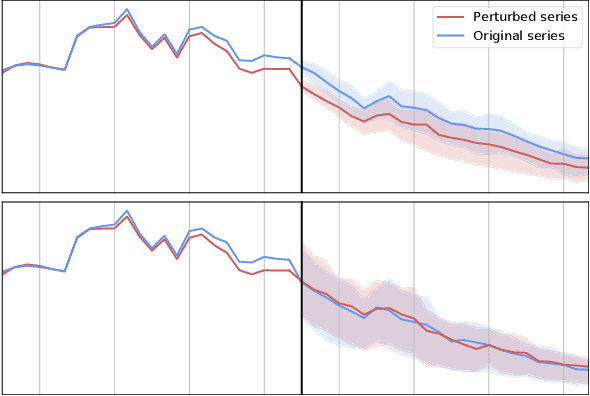
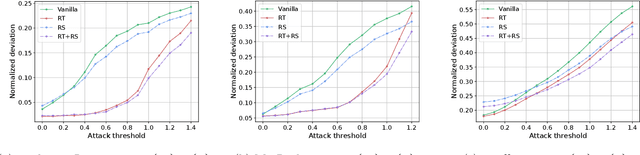
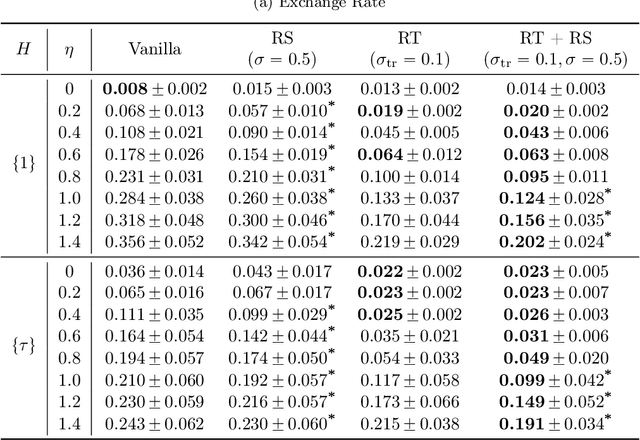
Probabilistic time series forecasting has played critical role in decision-making processes due to its capability to quantify uncertainties. Deep forecasting models, however, could be prone to input perturbations, and the notion of such perturbations, together with that of robustness, has not even been completely established in the regime of probabilistic forecasting. In this work, we propose a framework for robust probabilistic time series forecasting. First, we generalize the concept of adversarial input perturbations, based on which we formulate the concept of robustness in terms of bounded Wasserstein deviation. Then we extend the randomized smoothing technique to attain robust probabilistic forecasters with theoretical robustness certificates against certain classes of adversarial perturbations. Lastly, extensive experiments demonstrate that our methods are empirically effective in enhancing the forecast quality under additive adversarial attacks and forecast consistency under supplement of noisy observations.