Remove that Square Root: A New Efficient Scale-Invariant Version of AdaGrad

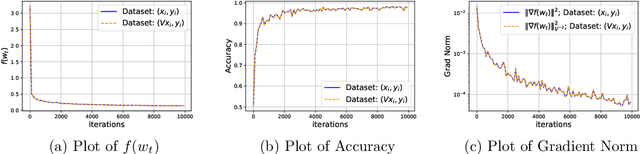
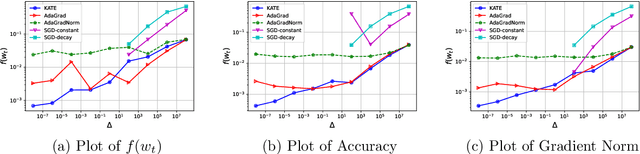
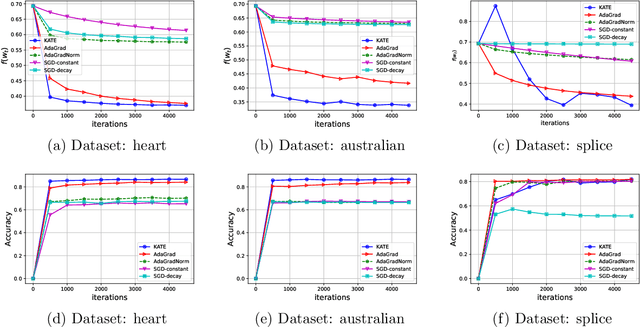
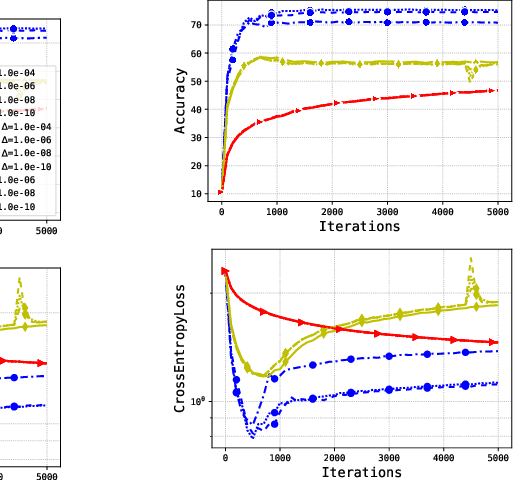
Adaptive methods are extremely popular in machine learning as they make learning rate tuning less expensive. This paper introduces a novel optimization algorithm named KATE, which presents a scale-invariant adaptation of the well-known AdaGrad algorithm. We prove the scale-invariance of KATE for the case of Generalized Linear Models. Moreover, for general smooth non-convex problems, we establish a convergence rate of $O \left(\frac{\log T}{\sqrt{T}} \right)$ for KATE, matching the best-known ones for AdaGrad and Adam. We also compare KATE to other state-of-the-art adaptive algorithms Adam and AdaGrad in numerical experiments with different problems, including complex machine learning tasks like image classification and text classification on real data. The results indicate that KATE consistently outperforms AdaGrad and matches/surpasses the performance of Adam in all considered scenarios.

Communication-Efficient Gradient Descent-Accent Methods for Distributed Variational Inequalities: Unified Analysis and Local Updates

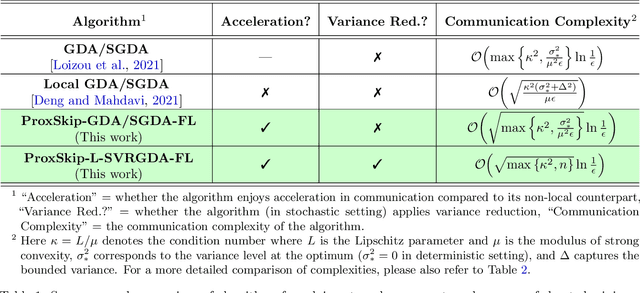
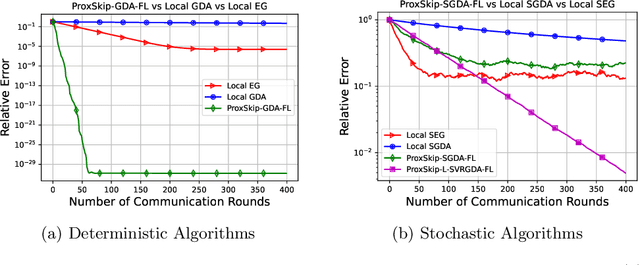
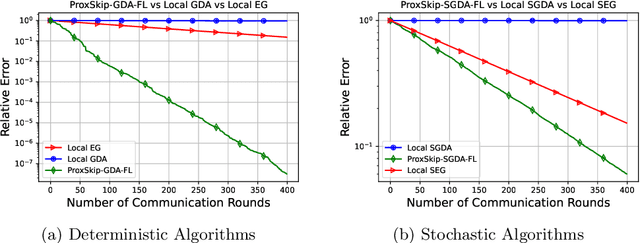
Distributed and federated learning algorithms and techniques associated primarily with minimization problems. However, with the increase of minimax optimization and variational inequality problems in machine learning, the necessity of designing efficient distributed/federated learning approaches for these problems is becoming more apparent. In this paper, we provide a unified convergence analysis of communication-efficient local training methods for distributed variational inequality problems (VIPs). Our approach is based on a general key assumption on the stochastic estimates that allows us to propose and analyze several novel local training algorithms under a single framework for solving a class of structured non-monotone VIPs. We present the first local gradient descent-accent algorithms with provable improved communication complexity for solving distributed variational inequalities on heterogeneous data. The general algorithmic framework recovers state-of-the-art algorithms and their sharp convergence guarantees when the setting is specialized to minimization or minimax optimization problems. Finally, we demonstrate the strong performance of the proposed algorithms compared to state-of-the-art methods when solving federated minimax optimization problems.

Single-Call Stochastic Extragradient Methods for Structured Non-monotone Variational Inequalities: Improved Analysis under Weaker Conditions

Single-call stochastic extragradient methods, like stochastic past extragradient (SPEG) and stochastic optimistic gradient (SOG), have gained a lot of interest in recent years and are one of the most efficient algorithms for solving large-scale min-max optimization and variational inequalities problems (VIP) appearing in various machine learning tasks. However, despite their undoubted popularity, current convergence analyses of SPEG and SOG require a bounded variance assumption. In addition, several important questions regarding the convergence properties of these methods are still open, including mini-batching, efficient step-size selection, and convergence guarantees under different sampling strategies. In this work, we address these questions and provide convergence guarantees for two large classes of structured non-monotone VIPs: (i) quasi-strongly monotone problems (a generalization of strongly monotone problems) and (ii) weak Minty variational inequalities (a generalization of monotone and Minty VIPs). We introduce the expected residual condition, explain its benefits, and show how it can be used to obtain a strictly weaker bound than previously used growth conditions, expected co-coercivity, or bounded variance assumptions. Equipped with this condition, we provide theoretical guarantees for the convergence of single-call extragradient methods for different step-size selections, including constant, decreasing, and step-size-switching rules. Furthermore, our convergence analysis holds under the arbitrary sampling paradigm, which includes importance sampling and various mini-batching strategies as special cases.

Chaos and Complexity from Quantum Neural Network: A study with Diffusion Metric in Machine Learning

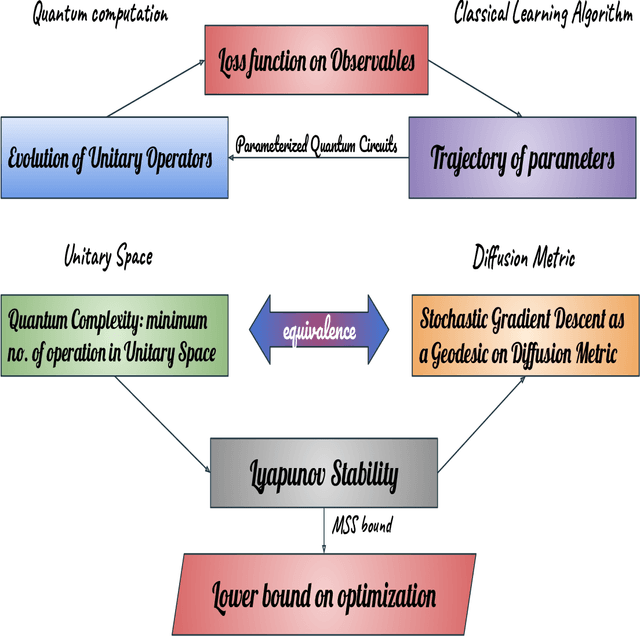
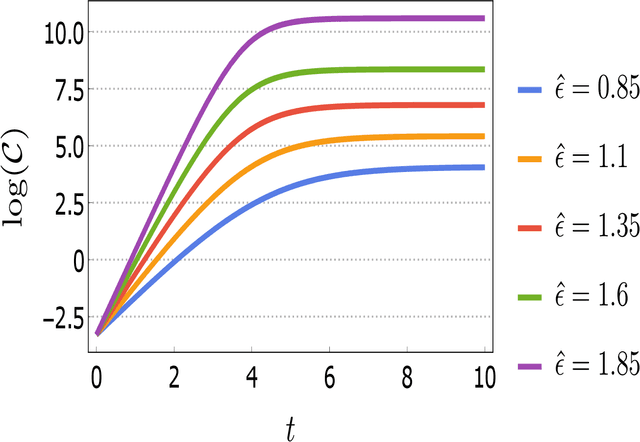
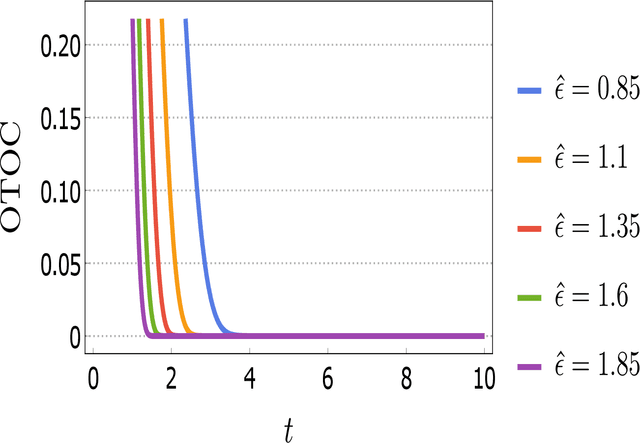
In this work, our prime objective is to study the phenomena of quantum chaos and complexity in the machine learning dynamics of Quantum Neural Network (QNN). A Parameterized Quantum Circuits (PQCs) in the hybrid quantum-classical framework is introduced as a universal function approximator to perform optimization with Stochastic Gradient Descent (SGD). We employ a statistical and differential geometric approach to study the learning theory of QNN. The evolution of parametrized unitary operators is correlated with the trajectory of parameters in the Diffusion metric. We establish the parametrized version of Quantum Complexity and Quantum Chaos in terms of physically relevant quantities, which are not only essential in determining the stability, but also essential in providing a very significant lower bound to the generalization capability of QNN. We explicitly prove that when the system executes limit cycles or oscillations in the phase space, the generalization capability of QNN is maximized. Moreover, a lower bound on the optimization rate is determined using the well known Maldacena Shenker Stanford (MSS) bound on the Quantum Lyapunov exponent.